Barisan dan deret geometri: Rumus, contoh soal dan pembahasan

Matematika Dasar » Barisan dan Deret › Barisan dan deret geometri: Rumus, contoh soal dan pembahasan

Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Barisan dan deret geometri: Rumus, contoh soal dan pembahasan

Barisan geometri adalah suatu barisan yang tersusun dengan suatu pola yang teratur yakni setiap suku berikutnya setelah suku pertama merupakan perkalian suku sebelumnya dengan suatu bilangan yang tetap.

Barisan merupakan urutan dari suatu bilangan berdasarkan aturan atau pola tertentu. Sama seperti himpunan, suatu barisan juga mempunyai anggota (elemen) yang biasanya disebut suku. Perhatikan contoh barisan yang terdiri dari 10 suku berikut.

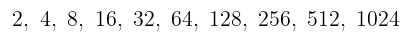
Suku pertama dari barisan tersebut adalah 2 dan suku kedua yaitu 4 dan demikian seterusnya hingga suku terakhirnya adalah 1024. Suku pertama suatu barisan sering dinotasikan dengan \(a\) atau \(U_1\), sedangkan suku ke-\(n\) dari suatu barisan dinyatakan dengan \(U_n\).

Perhatikan kembali barisan yang diberikan di atas. Anda bisa melihat bahwa barisan tersebut tersusun dengan suatu pola yang teratur, yakni setiap suku berikutnya setelah suku pertama merupakan perkalian antara suku sebelumnya dengan suatu bilangan yang tetap yakni 2. Bilangan yang tetap tersebut sering dinotasikan dengan huruf \(r\) yang menyatakan rasio dari barisan tersebut. Barisan yang demikian, kita sebut barisan geometri. Sedangkan deret geometri adalah penjumlahan suku-suku dari barisan geometri.

Jadi, barisan geometri adalah suatu barisan yang tersusun dengan suatu pola yang teratur yakni setiap suku berikutnya setelah suku pertama merupakan perkalian suku sebelumnya dengan suatu bilangan yang tetap (\(r\)).

Rumus rasio dan suku ke-\(n\) barisan geometri

Rasio dari barisan geometri dapat dicari dengan:

\[ r = \frac{U_2}{U_1} = \frac{U_3}{U_2} = \frac{U_4}{U_3} = \cdots = \frac{U_n}{U_{n-1}} \]

Sebagai contoh, dari barisan geometri yang diberikan di awal artikel ini, rasionya adalah

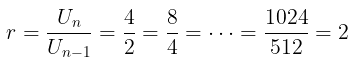
Rumus suku ke-\(n\) dari barisan geometri jika diketahui nilai suku ke-\(k\) dan rasio antar suku yang berdekatan (\(r\)), yaitu:

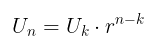
Jika yang diketahui adalah nilai suku pertama (\(a\)) yakni \( a = U_k; \ k =1 \) dan rasio antar sukunya (\(r\)), maka rumus \(U_n\) menjadi

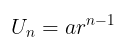
Rumus suku tengah barisan geometri

Terkadang dalam soal barisan geometri akan dijumpai permasalahan mencari suku tengah. Rumus untuk mencari suku tengah barisan geometri, yaitu:

\begin{aligned} U_t^2 &= U_1 \times U_n = a \times U_n \quad \text{atau} \\[8pt] U_t &= \sqrt{U_1 \times U_n}=\sqrt{a \times U_n}; \\[8pt] &\text{di mana} \ t = \frac{n+1}{2} \end{aligned}

Keterangan: \( U_t \) adalah suku tengah barisan geometri dan \( a = U_1 \) adalah suku pertama barisan geometri

Rumus jumlah \(n\) suku pertama barisan geometri

Deret geometri adalah penjumlahan suku-suku dari suatu barisan geometri. Penjumlahan suku pertama hingga suku ke-\(n\) dari barisan geometri diberikan oleh:

atau dapat dinyatakn sebagai

Jika diketahui suku pertama dan rasio dari barisan geometri, maka kita peroleh deret geometri dengan rumus:

\begin{aligned} S_n &= \frac{a(1-r^n)}{(1-r)}; \quad \text{untuk} \ 0 < r < 1 \\[8pt] S_n &= \frac{a(r^n-1)}{(r-1)}; \quad \text{untuk} \ r > 1 \end{aligned}

Sama seperti pada barisan aritmatika, kita dapat peroleh suku ke-\(n\) barisan geometri dengan mengurangkan jumlah suku ke-\(n\) dengan jumlah suku ke-\((n-1)\), yakni:

Rumus sisipan barisan geometri

Sisipan pada barisan geometri adalah menambahkan beberapa buah bilangan di antara dua suku yang berurutan pada suatu barisan geometri sehingga terbentuk barisan geometri yang baru. Setelah disispkan beberapa bilangan, maka rasio pada barisan geometri yang baru dapat dicari dengan dua kondisi.

Jika banyak bilangan yang disisipkan \((k)\) adalah genap, maka:

\[ r' = \pm \sqrt[k+1]{ \frac{U_n}{a} } \]

Jika banyak bilangan yang disisipkan \((k)\) adalah ganjil, maka:

\[ r' = \pm \sqrt[k+1]{ \frac{U_n}{a} } \]

Keterangan: \( r' \) adalah rasio dari barisan geometri yang baru; \(r\) adalah rasio dari barisan geometri sebelumnya; \(k\) adalah banyaknya bilangan yang disisipkan; \(a\) dan \(U_n\) adalah dua suku yang diantaranya disisipkan \(k\) bilangan.

Contoh soal barisan dan deret geometri

Setelah memahami pengertian barisan dan deret geometri di atas beserta rumus-rumusnya, berikut ini kita akan membahas beberapa contoh soal terkait barisan dan deret geometri.

Contoh 1:

Diketahui suku ke-5 dari barisan geometri adalah 243 dan hasil bagi suku ke-9 dengan suku ke-6 adalah 27. Tentukanlah suku ke-2 dari barisan geometri tersebut.

Pembahasan »

Dari soal diketahui bahwa

Untuk mencari suku ke-2, kita perlu mencari suku pertama (a) dan rasio barisan geometri tersebut (r). Ingat kembali bahwa \( U_n = ar^{n-1} \). Dengan demikian, kita peroleh

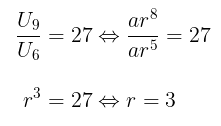
Substitusikan \(r = 3\) ke persamaan \( ar^4 = 243 \) sehingga

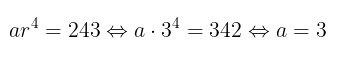
Jadi, suku ke-2 barisan geometri tersebut adalah

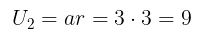
Jawaban D.

Contoh 2:

Jika jumlah 2 suku pertama deret geometri adalah 6 dan jumlah 4 suku pertama adalah 54. Tentukanlah jumlah 6 suku pertama deret tersebut (memiliki rasio positif)!

3.066/7
3.166/7
3.266/7
3.366/7
3.466/7

Pembahasan »

Dari soal diketahui bahwa \( S_2 = 6 \) sehingga diperoleh:

Selain itu, dari soal juga \( S_4 = 54 \), sehingga:

Jika persamaan (i) disubstitusikan ke persamaan (ii), maka diperoleh:

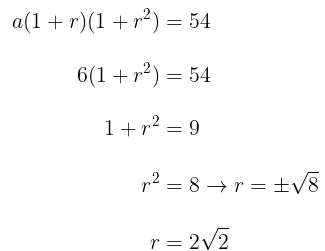
Perhatikan bahwa rasio bisa bernilai positif dan negatif, tapi dari soal diketahui bahwa rasio bernilai positif sehingga kita memilih rasio positif.

Selanjutnya, dengan mensubstitusi \( r = 2\sqrt{2} \) ke persamaan (i), maka:

Dengan demikian, jumlah 6 suku pertamanya adalah:

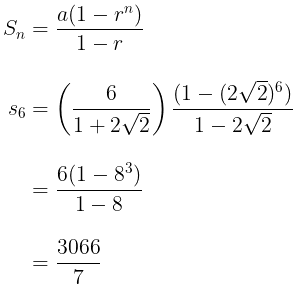
Jawaban A.

Contoh 3:

Diketahui deret geometri dengan suku pertama 6 dan suku keempat adalah 48. Jumlah enam suku pertama deret tersebut adalah…

Pembahasan »

Diketahui \( a = 6 \) dan \( U_4 = 48 \). Dengan \( U_n = ar^{n-1} \), maka dapat kita peroleh:

\begin{aligned} U_n = ar^{n-1} \Leftrightarrow U_4 &= 6 \cdot r^{4-1} \\[8pt] 48 &= 6r^3 \Rightarrow r = \frac{48}{6}=8 \\[8pt] r &= \sqrt[3]{8} = 2 \\[8pt] S_n = \frac{a(r^n-1)}{r-1} &= \frac{6(2^6-1)}{2-1} \\[8pt] S_n &= 6(64-1) = 6 \cdot 63 \\[8pt] &= 378 \end{aligned}

Jawaban C.

Contoh 4:

Diketahui barisan \( 2\sqrt{2}, 4, 4\sqrt{2}, 8, \cdots \). Suku keberapakah 128?

Pembahasan »

Dari barisan \( 2\sqrt{2}, 4, 4\sqrt{2}, 8, \cdots \) dapat kita peroleh:

\begin{aligned} r = \frac{U_n}{U_{n-1}} &= \frac{U_3}{U_2} = \frac{4\sqrt{2}}{4} = \sqrt{2} \\[8pt] U_n = ar^{n-1} &\Leftrightarrow 128 = 2\sqrt{2} \cdot (\sqrt{2})^{n-1} \\[8pt] &\Leftrightarrow 128 = 2\sqrt{2} \cdot \frac{(\sqrt{2})^n}{\sqrt{2}} = 2(\sqrt{2})^n \\[8pt] &\Leftrightarrow 64 = (\sqrt{2})^n \Rightarrow 64 = \left( 2^{\frac{1}{2}} \right)^n \\[8pt] &\Leftrightarrow 2^6 = 2^{\frac{1}{2}n} \Rightarrow 6 = \frac{1}{2}n \\[8pt] &\Leftrightarrow n = 12 \end{aligned}

Jawaban B.

Contoh 5:

Suku ke-\(n\) suatu deret geometri adalah \(4^{-n}\). Jumlah tak hingga deret tersebut sama dengan…

Pembahasan »

Diketahui \( U_n = 4^{-n} \) sehingga diperoleh:

\begin{aligned} U_n = 4^{-n} &\Leftrightarrow a=U_1 = 4^{-1} = \frac{1}{4} \\[8pt] &\Leftrightarrow U_2 = 4^{-2} = \frac{1}{16} \\[8pt] &\Leftrightarrow r = \frac{U_2}{U_1} = \frac{1/16}{1/4} = \frac{1}{4} \\[8pt] S_\infty = \frac{a}{1-r} &\Leftrightarrow S_\infty = \frac{1/4}{1-1/4} = \frac{1/4}{3/4} = \frac{1}{3} \end{aligned}

Jawaban E.

Contoh 6: UN 2010

Tiga buah bilangan membentuk barisan aritmetika dengan beda tiga. Jika suku kedua dikurangi 1, maka terbentuklah barisan geometri dengan jumlah 14. Rasio barisan tersebut adalah…

4
2
1/2
-1/2
-2

Pembahasan »

Misalkan tiga buah bilangan yang membentuk barisan aritmetika tersebut adalah \( x-3, x, x+3 \). Jika suku kedua dikurangi 1, maka terbentuk barisan geometri (x-3), (x-1), (x+3) dengan jumlah 14, sehingga kita peroleh berikut:

\begin{aligned} U_1+U_2+U_3 &= 14 \\[8pt] (x-3)+(x-1)+(x+3) &= 14 \\[8pt] 3x-1 &= 14 \\[8pt] 3x &= 14+1 \\[8pt] x &= \frac{15}{3}=5 \\[8pt] U_1 = x-3 &= 5-3 =2 \\[8pt] U_2 = x-1 &= 5-1 = 4 \\[8pt] r &= \frac{U_2}{U_1} = \frac{4}{2}=2 \end{aligned}

Jawaban B.

Contoh 7: SNMPTN 2009

Misalkan \( U_n \) menyatakan suku ke-n suatu barisan geometri. Jika diketahui \( U_5 = 12 \) dan \( \log U_4 + \log U_5 - \log U_6 = \log 3 \), maka nilai \( U_4 \) adalah…

Pembahasan »

Diketahui \( U_5 = 12 \) sehingga diperoleh \( ar^4 = 12 \) atau \( r^2 \) dan dari \( \log U_4 + \log U_5 - \log U_6 = \log 3 \), diperoleh:

\begin{aligned} \log U_4 + \log U_5 - \log U_6 &= \log 3 \\[8pt] \log \frac{U_4 \cdot U_5}{U_6} &= \log 3 \\[8pt] \log \frac{ar^3 \cdot ar^4}{ar^5} &= \log 3 \\[8pt] ar^2 &= 3 \\[8pt] ar^4 = 12 \Leftrightarrow ar^2 \cdot r^2 &= 12 \\[8pt] 3r^2 &= 12 \\[8pt] r &= 2 \\[8pt] r = 2 \Rightarrow ar^2 &= 3 \\[8pt] a \cdot 4 = 3 \Leftrightarrow a &= \frac{3}{4} \\[8pt] U_4 = ar^3 = \frac{3}{4} \cdot 2^3 = \frac{3}{4} \cdot 8 &= 6 \end{aligned}

Jawaban D.

Contoh 8: SBMPTN 2018

Diketahui barisan geometri \( u_n \) dengan \( u_3+u_4 = 9(u_1+u_2) \) dan \( u_1u_4 = 18u_2 \). Jumlah 4 suku pertama yang mungkin adalah…

Pembahasan »

Dari \( u_3+u_4 = 9(u_1+u_2) \) diperoleh:

\begin{aligned} U_3+U_4 &= 9(U_1+U_2) \\[8pt] ar^2+ar^3 &= 9(a+ar) \\[8pt] ar^2(1+r) &= 9a(1+r) \\[8pt] r^2 &= 9 \\[8pt] r &= \pm 3 \end{aligned}

Dari \( u_1u_4 = 18u_2 \), diperoleh:

\begin{aligned} u_1u_4 &= 18u_2 \\[8pt] a \cdot ar^3 &= 18 \cdot ar \\[8pt] a \cdot 9 &= 18 \\[8pt] a &= \frac{18}{9} = 2 \end{aligned}

Dengan demikian, jumlah 4 suku pertama barisan geometri tersebut, yaitu:

\begin{aligned} S_n = \frac{a(r^n-1)}{r-1} \Leftrightarrow S_4 &= \frac{2(3^4-1)}{3-1} = \frac{2(81-1)}{2} \\[8pt] S_4 &= 80 \end{aligned}

Jawaban D.

Contoh 9: SBMPTN 2014

Jika \( a_1, a_2, a_3 \) adalah barisan aritmatika dan \(a_1, a_2, a_1+a_3\) adalah barisan geometri, maka \( \frac{a_3}{a_1} = \cdots \)

Pembahasan »

Dari barisan aritmatika \( a_1, a_2, a_3 \) diperoleh \( 2a_2 = a_1+a_3 \) dan dari barisan geometri \(a_1, a_2, a_1+a_3\), kita peroleh:

\begin{aligned} a_2^2 &= a_1 \cdot (a_1+a_3) \\[8pt] a_2^2 &= a_1 \cdot (2a_2) \\[8pt] a_2 &= 2a_1 \end{aligned}

Persamaan yang kita peroleh di atas kita substitusi ke persamaan \( 2a_2 = a_1+a_3 \) sehingga didapatkan hasil berikut:

\begin{aligned} 2a_2 &= a_1+a_3 \\[8pt] 2(2a_1) &= a_1+a_3 \\[8pt] 4a_1 &= a_1+a_3 \\[8pt] 3a_1 &= a_3 \\[8pt] \frac{a_3}{a_1} &= \frac{3}{1} = 3 \end{aligned}

Jawaban C.

Contoh 10: SNMPTN 2012

Jika \(a\) adalah suku pertama, \(r\) adalah rasio, dan \( S_n = 5^{n+2}-25 \) adalah jumlah n suku pertama deret geometri maka nilai \(a+r=\cdots\)

Pembahasan »

Diketahui \( S_n = 5^{n+2}-25 \) sehingga kita peroleh berikut:

\begin{aligned} S_n &= 5^{n+2}-25 \\[8pt] \frac{a(r^n-1)}{r-1} &= 5^2 \cdot 5^n-5^2 \\[8pt] \left( \frac{a}{r-1} \right) r^n-\frac{a}{r-1} &= 25 \cdot 5^n - 25 \\[8pt] r^n &= 5^n \Leftrightarrow r = 5 \\[8pt] \frac{a}{r-1} &= 25 \Leftrightarrow \frac{a}{5-1} = 25 \\[8pt] a &= 25 \times 4 = 100 \\[8pt] a+r &= 100+r = 105 \end{aligned}

Jawaban B.

Contoh 11: UN 2012

Suku ke-3 dan suku ke-7 suatu deret geometri berturut-turut adalah 16 dan 256. Jumlah 7 suku pertama deret tersebut adalah…

Pembahasan »

Pertama kita tentukan dulu rasio dan suku pertama deret tersebut yaitu:

\begin{aligned} \frac{U_7}{U_3} = \frac{ar^6}{ar^2} &= \frac{256}{16} \\[8pt] r^4 &= 16 \\[8pt] r &= 2 \\[8pt] U_3 = ar^2 &\Leftrightarrow 16 = a \cdot 2^2 \\[8pt] a &= \frac{16}{4} = 4 \end{aligned}

Dengan demikian, jumlah 7 suku pertama deret tersebut yaitu:

\begin{aligned} S_n &= \frac{a(r^n-1)}{r-1} \\[8pt] S_7 &= \frac{4 \ (2^7-1)}{2-1} = \frac{4 (128-1)}{1} \\[8pt] &= 4 \cdot 127 \\[8pt] &= 508 \end{aligned}

Jawaban C.

Contoh 12: UM UGM 2013

Jumlah n suku pertama suatu deret aritmetika dinotasikan dengan \( S_n \). Jika suku pertama deret tersebut tak nol dan \( S_4, S_8, S_{16} \) membentuk barisan geometri maka \( \frac{S_8}{S_4} = \cdots \)

Pembahasan »

Dari soal diketahui bahwa \( S_n \) termasuk deret aritmetika dan \( S_4, S_8, S_{16} \) membentuk barisan geometri sehingga dapat kita peroleh berikut:

\begin{aligned} S_n &= \frac{n}{2}(2a+(n-1)b) \\[8pt] S_4 &= 2(2a+3b) \\[8pt] S_8 &= 4(2a+7b) \\[8pt] S_{16} &= 8(2a+15b) \\[8pt] S_8^2 &= S_4 \cdot S_{16} \\[8pt] \left( 4(2a+7b) \right)^2 &= 2(2a+3b) \cdot 8(2a+15b) \\[8pt] 16(2a+7b)^2 &= 16(2a+3b)(2a+15b) \\[8pt] 4a^2+28ab+49b^2 &= 4a^2+36ab+45b^2 \\[8pt] 4b^2 &= 8ab \\[8pt] b &= 2a \end{aligned}

Dari hasil di atas, kita dapat tentukan nilai \( \frac{S_8}{S_4} \), yaitu:

\begin{aligned} \frac{S_8}{S_4} &= \frac{4(2a+7b)}{2(2a+3b)} = \frac{2(2a+7 \cdot 2a)}{2a+3 \cdot 2a} \\[8pt] &= \frac{2(16a)}{8a} = \frac{32a}{8a} \\[8pt] &= 4 \end{aligned}

Jawaban B.

Contoh 13: UN 1993

Suku pertama dan rasio barisan geometri berturut-turut 2 dan 3. Jika jumlah n suku pertama deret tersebut adalah 80, banyak suku barisan tersebut adalah…

Pembahasan »

Diketahui \(a = 2, r = 3\) dan \(S_n = 80\). Banyak suku barisan tersebut dapat dicari sebagai berikut:

\begin{aligned} S_n &= \frac{a(r^n-1)}{r-1} \Leftrightarrow 80 = \frac{2(3^n-1)}{3-1} \\[8pt] 80 &= 3^n-1 \Leftrightarrow 3^n = 81 \\[8pt] n &= 4 \end{aligned}

Jawaban B.

Contoh 14: UN 2014

Jumlah konsumsi gula pasir oleh penduduk suatu kelurahan pada tahun 2013 sebesar 1000 kg dan selalu meningkat dua kali lipat setiap tahun. Total konsumsi gula penduduk tersebut pada tahun 2013 sampai dengan tahun 2018 adalah…

62.000 kg
63.000 kg
64.000 kg
65.000 kg
66.000 kg

Pembahasan »

Kita dapat menyelesaikan soal ini menggunakan konsep barisan dan deret geometri. Dari narasi “meningkat dua kali lipat setiap tahun” artinya rasio sama dengan 2. Nilai suku pertama \(a\) sama dengan 1000 dan \(n = 6\) tahun (2013-2018).

Dengan demikian, total konsumsi gula penduduk tersebut pada tahun 2013 sampai denegan 2018, yaitu:

\begin{aligned} S_n &= \frac{a(r^n-1)}{r-1} \Leftrightarrow S_6 = \frac{1.000(2^6-1)}{2-1} \\[8pt] &= \frac{1.000(64-1)}{1} = 1000(63) \\[8pt] &= 63.000 \ \text{kg} \end{aligned}

Jawaban B.

Contoh 15:

Dari suatu barisan geometri diketahui suku ke-2 adalah 4/3 dan suku ke-5 adalah 36. Suku ke-6 barisan tersebut adalah…

Pembahasan »

Diketahui \(U_2 = 34\) dan \(U_5 = 36\) sehingga:

\begin{aligned} U_n &= ar^{n-1} \\[8pt] U_2 &= ar \Leftrightarrow \frac{4}{3} = ar \\[8pt] U_5 &= ar^4 \Leftrightarrow 36 = ar^4 \\[8pt] \frac{U_5}{U_2} &= \frac{ar^4}{ar} \Leftrightarrow \frac{36}{4/3} = r^3 \\[8pt] r^3 &= 27 \Leftrightarrow r = 3 \\[8pt] ar &= \frac{4}{3} \Leftrightarrow 3a = \frac{4}{3} \\[8pt] a &= \frac{4/3}{3} = \frac{4}{9} \\[8pt] U_6 &= ar^5 = \frac{4}{9} \cdot 3^5 = \frac{4}{9} \times 243 \\[8pt] &= 108 \end{aligned}

Jawaban A.

Contoh 16:

Tiga buah bilangan membentuk barisan geometri. Jika jumlah ketiga bilangan itu 13 dan hasil kalinya 27, maka suku ke-3 adalah…

Pembahasan »

Misalkan tiga bilangan yang membentuk barisan geometri tersebut yaitu \( \frac{a}{r}, a, ar\), sehingga diperoleh:

\begin{aligned} \frac{a}{r} \cdot a \cdot ar = 27 &\Leftrightarrow a^3 = 27 \\[8pt] &\Leftrightarrow a=\sqrt[3]{27} = 3 \\[8pt] \frac{a}{r} + a + ar = 13 &\Leftrightarrow \frac{3}{r} + 3 + 3r = 13 \\[8pt] &\Leftrightarrow \frac{3}{r}+3r=10 \\[8pt] &\Leftrightarrow 3+3r^2=10r \\[8pt] &\Leftrightarrow 3r^2-10r+3 = 0 \\[8pt] &\Leftrightarrow (3r-1)(r-3) = 0 \\[8pt] &\Leftrightarrow r = \frac{1}{3} \ \text{atau} \ r = 3 \end{aligned}

Untuk \( r = 3\), maka barisan geometri tersebut yaitu: 1, 3, dan 9. Sementara, jika \( r = \frac{1}{3} \) maka barisan geometri tersebut yaitu: 9, 3, dan 1. Dengan demikian, suku ke-3 sesuai pilihan pada soal yaitu 9.

Jawaban D.

Contoh 17:

Suku pertama dan kedua suatu deret geometri berturut-turut adalah \( p^{-4} \) dan \(p^x\). Jika suku ke-8 adalah \( p^{52} \) maka nilai \(x= \cdots\)

Pembahasan »

Dari suku pertama \( p^{-4} \) dan suku kedua \(p^x\) suatu deret geometri, diperoleh:

\begin{aligned} r &= \frac{U_n}{U_{n-1}} = \frac{U_2}{U_1} = \frac{p^x}{p^{-4}} = p^{x+4} \\[8pt] U_n &= ar^{n-1} \Leftrightarrow U_8 = p^{-4} \cdot (p^{x+4})^{8-1} \\[8pt] p^{52} &= p^{-4} \cdot p^{7x+28} \Leftrightarrow p^{52} = p^{7x+24} \\[8pt] 52 &= 7x+24 \Leftrightarrow 7x = 28 \\[8pt] x &= \frac{28}{7} = 4 \end{aligned}

Jawaban D.

Contoh 18:

Diketahui barisan \( 2, 2\sqrt{2}, 4, 4\sqrt{2}, \cdots \). Suku keberapakah \( 64\sqrt{2} \) ?

Pembahasan »

Untuk menyelesaikan soal ini, kita dapatkan rasio barisannya dulu dan kemudian gunakan rumus \( U_n = ar^{n-1} \) untuk mencari \(n\) atau suku ke sekian. Kita dapatkan hasil berikut:

\begin{aligned} r = \frac{U_n}{U_{n-1}} = \frac{U_2}{U_1} = \frac{2\sqrt{2}}{2} &= \sqrt{2} \\[8pt] U_n = ar^{n-1} \Leftrightarrow 64\sqrt{2} &= 2 (\sqrt{2})^{n-1} \\[8pt] 32\sqrt{2} &= (\sqrt{2})^n \cdot (\sqrt{2})^{-1} \\[8pt] 2^5 \cdot 2^{\frac{1}{2}} &= 2^{\frac{1}{2}n} \cdot 2^{-\frac{1}{2}} \\[8pt] 2^{\frac{11}{2}} &= 2^{\frac{1}{2}n-\frac{1}{2}} \\[8pt] \frac{11}{2} &= \frac{1}{2}n-\frac{1}{2} \\[8pt] \frac{1}{2}n &= \frac{11}{2}+\frac{1}{2} \\[8pt] \frac{1}{2}n &= 6 \\[8pt] n &= 12 \end{aligned}

Jawaban B.

Contoh 19:

Diketahui suatu barisan geometri dengan suku pertama \( \sqrt[3]{x} \) dan suku kedua \( \sqrt{x} \). Maka \(U_5\) sama dengan….

\( x \)
\( x^{\frac{1}{4}} \)
\( x^{\frac{2}{3}} \)
\( x^{\frac{1}{2}} \)
\( x^{\frac{1}{5}} \)

Pembahasan »

Dari soal diketahui \( a = U_1 = \sqrt[3]{x} \) dan \( U_2 = \sqrt{x} \). Untuk mencari suku ke lima atau \( U_5 \), kita perlu cari dulu rasio deretnya dan kemudian gunakan rumus suku ke-n. Berikut hasil yang diperoleh:

\begin{aligned} r = \frac{U_n}{U_{n-1}} = \frac{U_2}{U_1} = \frac{\sqrt{x}}{\sqrt[3]{x}} &= \frac{x^{\frac{1}{2}}}{x^{\frac{1}{3}}} = x^{\frac{1}{6}} \\[8pt] U_n = ar^{n-1} \Leftrightarrow U_5 &= \sqrt[3]{x} \cdot \left( x^\frac{1}{6} \right)^{5-1} \\[8pt] &= x^{\frac{1}{3}} \cdot x^{\frac{4}{6}} = x^{\frac{1}{3}} \cdot x^{\frac{2}{3}} \\[8pt] &= x^{\frac{1}{3}+\frac{2}{3}} = x \end{aligned}

Jawaban A.

Contoh 20:

Jika \( p\sqrt{q}, q\sqrt{p} \) merupakan dua suku pertama deret geometri, maka suku ke tiga adalah…

\( p\sqrt{p} \)
\( q\sqrt{q} \)
\( \sqrt{p} \)
\( \sqrt{q} \)
\( p \)

Pembahasan »

Dari soal diketahui \( a = U_1 = p\sqrt{q} \) dan \( U_2 = q\sqrt{p} \). Untuk menghitung suku ketiga kita perlu mencari rasio deretnya terlebih dahulu dan kemudian gunakan rumus suku ke-n. Berikut hasil yang diperoleh:

\begin{aligned} r = \frac{U_n}{U_{n-1}} = \frac{U_2}{U_1} = \frac{q\sqrt{p}}{p\sqrt{q}} &= \frac{\sqrt{q}}{\sqrt{p}}\\[8pt] U_n = ar^{n-1} \Leftrightarrow U_3 &= p\sqrt{q} \cdot \left( \frac{\sqrt{q}}{\sqrt{p}} \right)^{3-1} \\[8pt] &= p\sqrt{q} \cdot \left( \frac{\sqrt{q}}{\sqrt{p}} \right)^2 \\[8pt] &= p\sqrt{q} \cdot \frac{q}{p} \\[8pt] &= q\sqrt{q} \end{aligned}

Jawaban B.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.

www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

Matematika Dasar » Barisan dan Deret › Barisan dan deret geometri: Rumus, contoh soal dan pembahasan