www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Turunan Fungsi › Turunan Komposisi Fungsi dan Aturan Rantai
Turunan Komposisi Fungsi dan Aturan Rantai
Fungsi komposisi dapat diartikan sebagai penggabungan dua jenis fungsi \(f(x)\) dan \(g(x)\) sehingga menghasilkan suatu fungsi baru. Turunan dari fungsi komposisi dapat diperoleh menggunakan aturan rantai.
Fungsi komposisi (composition function) dapat diartikan sebagai penggabungan dua jenis fungsi \(f(x)\) dan \(g(x)\) sehingga menghasilkan suatu fungsi baru. Sebagai contoh, fungsi \(f(x) = \sin x\) dan \(g(x)=x^2\) dapat digabung menjadi suatu fungsi baru yakni \(f(g(x)) = \sin x^2\).
Untuk mencari turunan (derivative) dari komposisi fungsi, kita dapat menggunakan aturan rantai (chain rule). Misalkan, anda diminta untuk mencari turunan dari fungsi berikut

Untuk mencari turunan fungsi ini tanpa menggunakan aturan rantai, pertama anda harus mengalikan bersama ke 60 faktor-faktor kuadrat \(2x^2 - 4x + 1\) dan kemudian mendiferensialkan polinom derajat 120 yang dihasilkan. Bayangkan betapa sulitnya mencari turunan untuk fungsi tersebut.
Untungnya, kita tidak perlu melakukan itu, karena terdapat cara yang lebih baik yakni dengan menggunakan aturan rantai. Setelah anda mempelajari aturan rantai, anda akan mampu menuliskan jawaban untuk turunan fungsi di atas secara cepat, yakni
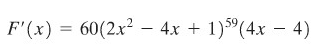
TEOREMA: Aturan Rantai
Andaikan \(y = f(u)\) dan \(u = g(x)\). Jika \(g\) terdiferensialkan di \(x\) dan \(f\) terdiferensialkan di \(u = g(x)\), maka fungsi komposit \((f \ o \ g)\), didefinisikan oleh \((f \ o \ g)(x) = f(g(x))\), terdiferensialkan di \(x\) dan

Yakni,

atau

Penerapan Aturan Rantai
Kita mulai dengan contoh fungsi yang diperkenalkan pada bagian awal di atas.
CONTOH 1:
Jika \( y = (2x^2 - 4x + 1)^{60}\), carilah \(D_x y\).
Penyelesaian:
Kita pikirkan ini sebagai

Fungsi yang luar adalah \(f(u) = u^{60}\) dan fungsi dalamnya adalah \(u = g(x) = 2x^2 - 4x + 1\). Dengan demikian,

CONTOH 2:
Jika \(y = 1/(2x^5 - 7)^3\), carilah dy/dx.
Penyelesaian:
Pikirkanlah begini

Sehingga,

CONTOH 3:

Penyelesaian:
Kita bisa memikirkan ini sebagai \(y=u^{13}\), di mana \(u=(t^3 - 2t + 1)/(t^4 + 3)\). Dengan menerapkan Aturan Rantai dan Aturan Hasilbagi, kita peroleh

Sumber:
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Education is the most powerful weapon which you can use to change the world.
