Integral Fungsi Trigonometri

Matematika Dasar » Integral › Integral Fungsi Trigonometri

Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Integral

Integral Fungsi Trigonometri

Selain fungsi aljabar, integral juga dapat dioperasikan pada fungsi trigonometri. Beberapa integral fungsi trigonometri dapat diperoleh dengan mudah berdasarkan informasi bahwa integral merupakan suatu anti turunan.

Oleh Tju Ji Long · Statistisi

Hub. WA: 0812-5632-4552

Selain fungsi aljabar, integral juga dapat dioperasikan pada suatu fungsi yang berupa fungsi trigonometri. Beberapa integral fungsi trigonometri dapat diperoleh dengan mudah berdasarkan informasi bahwa integral merupakan anti turunan atau kebalikan dari turunan, yakni

\[ \int D_x \left(f(x)\right) \ dx = f(x) \]

Kita tahu bahwa ketika suatu fungsi, katakanlah fungsi f(x), diturunkan atau didiferensialkan maka akan diperoleh suatu fungsi baru, katakanlah f'(x). Jika fungsi baru hasil turunan dari f(x) diintegralkan, maka kita akan memperoleh fungsi f(x) itu sendiri.

Perhatikan Tabel 1 berikut yang menunjukkan turunan dari beberapa fungsi trigonometri dan integralnya dengan memanfaatkan informasi bahwa integral merupakan suatu anti turunan.

Tabel 1. Fungsi f(x), turunannya dan anti turunan atau integral tak tentu dari fungsi f(x)

No	Fungsi f(x) = y	Turunan: dy/dx	Integral
1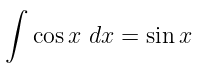
2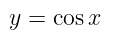
3
4
5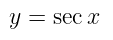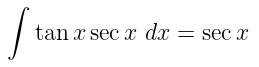
6

Integral Fungsi \( \tan x \) dan \( \cot x \)

Integral dari \( \tan x \) dan \( \cot x \) dapat dicari dengan memanfaatkan kesamaan bahwa \(\tan x = \frac{\sin x}{\cos x}\), lalu memakai teknik integral substitusi. Misalkan \(u = \cos x\), maka \(du = - \sin x \ dx\). Kita peroleh

Dengan cara serupa, misalkan \(u = \sin x\), maka \(du = \cos x \ dx\). Kita peroleh

Integral Fungsi \( \sec x \) dan \( \csc x \)

Untuk mencari integral \( \sec x \), kita pertama mengalikan fungsi \( \sec x \) dengan

Sehingga,

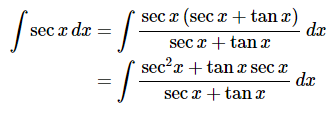
Dengan menerapkan teknik integral substitusi dan memisalkan \(u = \sec x + \tan x\). Kita peroleh

Dengan cara serupa untuk integral \(\sec x\), kita pertama mengalikan fungsi \(\csc x\) dengan

Sehingga,

Terapkan teknik integral substitusi. Misalkan \(u = \csc x + \cot x\), maka \(du = ( - \csc x \cot x – \csc^2 x) \ dx\). Kita peroleh

\begin{aligned} \int \csc x \ dx &= - \int \frac{(-\csc^2 x - \csc x \cot x)}{\csc x + \cot x} \ dx \\[8pt] &= -\int \frac{1}{u} \ du = - \ln |u| + C \\[8pt] &= -\ln|\csc x + \cot x| + C \end{aligned}

Contoh Soal dan Pembahasan

Contoh 1:

Hitunglah \( \int \cos(2x + 5) \ dx \).

Pembahasan:

Misalkan \( u = 2x + 5 \) maka

Sehinga diperoleh

Contoh 2:

Hitunglah \( \int (\sin 3x - \cos 3x)^2 \ dx \).

Pembahasan:

Pertama, kita jabarkan pangkat 2 kemudian sederhanakan. Kita peroleh

Contoh 3:

Hitunglah \( (\tan 2x - \sec 2x)^2 \ dx \).

Pembahasan:

Pertama, kita jabarkan pangkat 2 kemudian sederhanakan. Kita peroleh

Contoh 4:

Hitunglah \( \int 4 \sin 4x \cos 2x \ dx \).

Pembahasan:

Pertama kita sederhana fungsi dalam integral dengan memanfaatkan kesamaan identitas trigonometri. Kita peroleh

Contoh 5:

Hitunglah integral berikut ini

Pembahasan:

Cukup sekian penjelasan mengenai pengintegralan fungsi trigonometri dalam artikel ini. Semoga bermanfaat.

Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.

www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

MATEMATIKA DASAR

Matematika Dasar » Integral › Integral Fungsi Trigonometri

Integral