Barisan dan deret tak hingga: Rumus, contoh soal dan pembahasan

Matematika Dasar » Barisan dan Deret › Barisan dan deret tak hingga: Rumus, contoh soal dan pembahasan

Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Barisan dan deret tak hingga: Rumus, contoh soal dan pembahasan

Barisan tak hingga dapat didefinisikan sebagai barisan yang mana suku-sukunya tersusun hingga tak terhingga banyaknya.

Barisan merupakan urutan dari suatu bilangan yang tersusun berdasarkan aturan atau pola tertentu. Dengan demikian, barisan tak hingga dapat didefinisikan sebagai barisan yang mana suku-sukunya tersusun hingga tak terhingga banyaknya.

Ada dua istilah yang sering muncul menyangkut barisan atau deret tak hingga yaitu konvergen dan divergen. Kita membahasnya berikut ini.

Kekonvergenan Barisan Tak Hingga

Suatu barisan tak hingga dikatakan konvergen jika suku ke tak hingga dari barisan tersebut menuju ke suatu nilai tertentu. Sebaliknya, suatu barisan tak hingga dikatakan divergen jika suku ke tak hingga dari barisan tersebut tidak memusat pada suatu titik atau tidak menuju ke suatu titik tertentu.

Sekarang perhatikan empat barisan tak hingga yang diberikan di bawah ini beserta ilustrasinya pada Gambar 1.

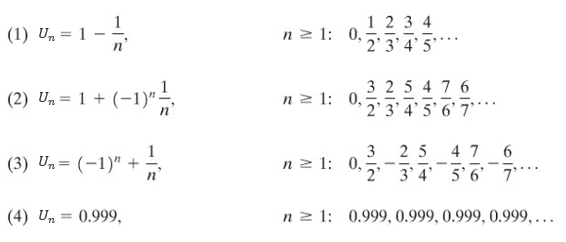
Gambar 1. Ilustrasi barisan tak hingga

Seperti terlihat pada Gambar 1, nilai suku-suku dalam tiap barisan semua konvergen menuju 1. Akan tetapi, apakah semua barisan tersebut benar-benar konvergen menuju 1? Tentu saja jika kita perhatikan dengan seksama, barisan (3) dan barisan (4) tidaklah demikian.

Agar suatu barisan dikatakan konvergen menuju 1, syaratnya ialah bahwa nilai-nilai barisan itu harus mendekati 1. Tapi tidak hanya harus mendekati satu, nilai-nilai tersebut juga harus tetap berdekatan yang mana tidak terpenuhi oleh barisan (3).

Selain itu, berdekatan artinya semakin lama semakin dekat dan ini tidak terpenuhi oleh barisan (4). Walaupun barisan (4) tidak konvergen menuju 1, kita masih dapat mengatakan bahwa barisan tersebut konvergen menuju 0,999. Sedangkan untuk barisan (3) tidak konvergen sama sekali atau kita katakan barisan tersebut sebagai barisan yang divergen.

Limit Barisan Tak Hingga

Sebagian besar akan setuju bahwa menentukan kekonvergenan suatu barisan tak hingga dengan membuat ilustrasi seperti ditampilkan pada Gambar 1 tidaklah efisien. Ada cara lain untuk menentukan kekonvergenan suatu barisan tak hingga yaitu dengan menggunakan konsep limit.

Definisi:

Suatu barisan tak hingga dikatakan konvergen jika limit barisan tersebut menuju ke suatu bilangan L yang berhingga. Sebaliknya, barisan tak hingga yang tidak konvergen ke suatu bilangan yang terhingga dikatakan divergen.

Contoh 1:

Misalkan diketahui suatu barisan dengan rumus suku ke-n diberikan oleh \( U_n = 1 - \frac{1}{n}; \ n \geq 1 \). Tentukan kekonvergenan barisan tersebut untuk \(n\) menuju tak hingga.

Pembahasan »

Perhatikan bahwa ini merupakan barisan (1) pada Gambar 1 di atas. Untuk menentukan konvergenan barisan ini, kita cukup mencari limit dari rumus barisan tersebut, yakni:

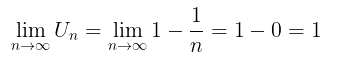
Jadi, barisan tak hingga tersebut konvergen ke 1. Hasil yang diperoleh ini sama dengan yang telah dibahas sebelumnya.

Kekonvergenan Deret Geometri Tak Hingga

Sebagaimana halnya barisan tak terhingga, pada deret tak terhingga juga terdapat deret tak terhingga konvergen dan deret tak terhingga divergen. Kekonvergenan deret tak hingga adalah topik yang cukup luas, tapi di sini kita hanya akan membahas kekonvergenan deret geometri tak terhingga.

Jika Anda tertarik untuk mengetahui lebih banyak tentang kekonvergenan deret tak hingga, Anda dapat membacanya pada materi kalkulus II di website ini.

Sekarang perhatikanlah deret geometri tak terhingga berikut ini

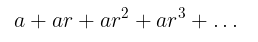
Kita tahu bahwa rumus untuk deret geometri adalah

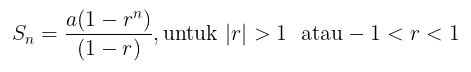
Dengan demikian, limit \(S_n\) untuk \(n\) mendekati tak terhingga \(( n \to \infty )\) adalah

Jadi, rumus untuk deret geometri tak terhingga adalah

Contoh 2:

Jika \( \frac{1}{p} + \frac{1}{q} = 1 \), maka jumlah deret geometri tak hingga \( \frac{1}{p} + \frac{1}{pq} + \frac{1}{pq^2} + \frac{1}{pq^3} + \dots \) adalah...

\( 1 \)
\( 1 \frac{1}{2} \)
\( \frac{1}{2} \)
\( \frac{q}{p} \)
\( \frac{p}{q} \)

Pembahasan »

Dari soal diketahui bahwa \( \frac{1}{p} + \frac{1}{q} = 1 \). Dengan melakukan sedikit modifikasi, kita peroleh:

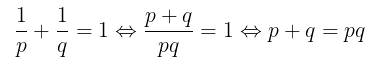
Selanjutnya, carilah rasio deret tersebut, yakni

Kita tahu bahwa rumus untuk jumlah deret tak hingga diberikan oleh:

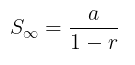
Dengan demikian, kita peroleh:

(Pada persamaan terakhir kita mengganti \(pq\) dengan \( p + q\) karena \( p+q = pq \))

Jawaban A.

Contoh 3:

Sebuah bola dijatuhkan ke lantai dari ketinggian 12 m. Jika setiap kali jatuh, bola memantul kembali ke atas dengan ketinggian 2/3 dari ketinggian sebelumnya, maka hitunglah panjang lintasan bola dari mulai dijatuhkan hingga berhenti!

18 m
20 m
36 m
40 m
60 m

Pembahasan »

Ini merupakan contoh kasus untuk deret geometri tak hingga. Perhatikan ilustrasi dari pantulan bola tersebut berikut ini:

Panjang lintasan bola dari mulai dijatuhkan hingga berhenti merupakan penjumlahan panjang lintasan ke bawah dan panjang lintasan ke atas. Untuk panjang lintasan ke bawah, diperoleh:

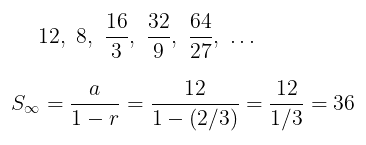
dan panjang lintasan bola ke atas adalah:

Jadi, total lintasan adalah 36 + 24 = 60 meter.

Jawaban E.

Contoh 4:

Suku ke-\(n\) suatu deret geometri adalah \(4^{-n}\). Jumlah tak hingga deret tersebut sama dengan…

Pembahasan »

Diketahui \( U_n = 4^{-n} \) sehingga diperoleh:

\begin{aligned} U_n = 4^{-n} &\Leftrightarrow a=U_1 = 4^{-1} = \frac{1}{4} \\[8pt] &\Leftrightarrow U_2 = 4^{-2} = \frac{1}{16} \\[8pt] &\Leftrightarrow r = \frac{U_2}{U_1} = \frac{1/16}{1/4} = \frac{1}{4} \\[8pt] S_\infty = \frac{a}{1-r} &\Leftrightarrow S_\infty = \frac{1/4}{1-1/4} = \frac{1/4}{3/4} = \frac{1}{3} \end{aligned}

Jawaban E.

Contoh 5:

Nilai dari \( 2^{1/4} \cdot 4^{1/16} \cdot 8^{1/48} \cdots \) adalah …

\( \sqrt{2} \)
\( 2^{1/4} \)
1
2
4

Pembahasan »

Untuk menjawab soal ini, kita dapat mengubah semua basis menjadi 2 seperti berikut:

\begin{aligned} 2^{1/4} \cdot 4^{1/16} \cdot 8^{1/48} \cdots &= 2^{1/4} \cdot (2^2)^{1/16} \cdot (2^3)^{1/48} \cdots \\[8pt] &= 2^{1/4} \cdot 2^{1/8} \cdot 2^{1/16} \cdots \\[8pt] &= 2^{1/4+1/8+1/16+\cdots} \end{aligned}

Perhatikan bahwa \( \frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\cdots \) merupakan deret geometri tak hingga dengan suku pertama \(a = \frac{1}{4}\) dan rasio \( r = \frac{1}{2}\). Hasil dari jumlah deret geometri tak hingga ini, yaitu:

\begin{aligned} S_\infty &= \frac{a}{1-r} = \frac{1/4}{1-1/2} \\[8pt] &= \frac{1/4}{1/2} = 1/2 \end{aligned}

Dengan demikian, kita peroleh:

\begin{aligned} 2^{1/4} \cdot 4^{1/16} \cdot 8^{1/48} \cdots &= 2^{1/4+1/8+1/16+\cdots} \\[8pt] &= 2^{1/2} = \sqrt{2} \end{aligned}

Jawaban A.

Contoh 6:

Nilai \( a \) yang memenuhi persamaan \( \frac{1}{ {}^{10} \! \log a } + \frac{1}{ {}^{\sqrt{10}} \! \log a } + \frac{1}{ {}^{ \sqrt{ \sqrt{10} } } \! \log a } + \cdots = 200 \) adalah…

\( \frac{1}{100} \)
\( \frac{1}{10} \)
\( \sqrt{10} \)
\( 10^{\frac{1}{100}} \)
\( 10^{\frac{1}{10}} \)

Pembahasan »

Ingat sifat logaritma berikut:

\begin{aligned} \frac{1}{{}^a \! \log b} &= {}^b \! \log a \\[8pt] {}^a \! \log b + {}^a \! \log c &= {}^a \! \log bc \end{aligned}

Berdasarkan sifat logaritma di atas, kita peroleh berikut:

\begin{aligned} \frac{1}{ {}^{10} \! \log a } + \frac{1}{ {}^{\sqrt{10}} \! \log a } + \frac{1}{ {}^{ \sqrt{ \sqrt{10} } } \! \log a } + \cdots &= 200 \\[8pt] {}^a \! \log 10 + {}^a \! \log \sqrt{10} + {}^a \! \log \sqrt{ \sqrt{10} } + \cdots &= 200 \\[8pt] {}^a \! \log \left( 10 \cdot \sqrt{10} + \sqrt{ \sqrt{10} } + \cdots \right) &= 200 \\[8pt] {}^a \! \log \left( 10^{1+\frac{1}{2}+\frac{1}{4}+\cdots} \right) &= 200 \end{aligned}

Perhatikan bahwa \( 1+\frac{1}{2}+\frac{1}{4}+\cdots \) merupakan deret geometri tak hingga dengan \(a = 1\) dan \(r = \frac{1}{2}\) sehingga:

\begin{aligned} S_\infty = \frac{a}{1-r} = \frac{1}{1-\frac{1}{2}} &= 2 \\[8pt] {}^a \! \log \left( 10^{1+\frac{1}{2}+\frac{1}{4}+\cdots} \right) &= 200 \\[8pt] {}^a \! \log \left( 10^2 \right) &= 200 \\[8pt] a^{200} &= 10^2 \\[8pt] a &= (10^2)^{\frac{1}{200}} \\[8pt] &= 10^{\frac{1}{100}} \end{aligned}

Jadi, nilai \(a\) yang memenuhi persamaan tersebut adalah \( 10^{ \frac{1}{100} } \).

Jawaban D.

Contoh 7: UTBK Tes Kompetensi Akademik SAINTEK 2019

Seseorang berjalan dengan kecepatan 60 km/jam selama satu jam pertama. Pada jam kedua, kecepatan berkurang menjadi seperempatnya demikian juga pada jam berikutnya. Jarak terjauh yang dapat ditempuh orang tersebut adalah … km.

Pembahasan »

Kita dapat menghitung jarak terjauh yang dapat ditempuh menggunakan konsep deret geometri tak hingga dengan suku pertama \(a = 60\) dan rasio \(r = \frac{1}{4}\).

Berdasarkan informasi pada soal, dapat kita tuliskan lintasan yang ditempuh dari jam pertama, jam kedua dan seterusnya, yaitu \( 60+\frac{60}{4}+\frac{60}{16}+\frac{60}{64}+\cdots \)

Dengan demikian, jarak terjauh yang dapat ditempuh, yaitu:

\begin{aligned} S_\infty &= \frac{a}{1-r} = \frac{60}{1-\frac{1}{4}} \\[8pt] &= \frac{60}{3/4} = 60 \times \frac{4}{3} \\[8pt] &= 80 \end{aligned}

Jawaban D.

Contoh 8: SBMPTN 2013

Parabola \( y = x^2-2x+3m-1 \) mempunyai titik puncak \( (p,q) \). Jika \(2p\) dan \( \frac{q}{4} \) dua suku pertama deret geometri tak hingga yang mempunyai jumlah 4, maka nilai \(m\) adalah…

- 3/2
2/3
1
2
3

Pembahasan »

Untuk menyelesaikan soal ini kita setidaknya perlu memahami rumus titik puncak fungsi kuadrat yaitu \( \left( -\frac{b}{2a}, -\frac{D}{4a} \right) \) dan jumlah deret geometri tak hingga yaitu \( S_\infty = \frac{a}{1-r} \).

Dari parabola \(y = x^2-2x+3m-1\) dapat kita tentukan:

\begin{aligned} p &= -\frac{b}{2a} = - \frac{-2}{2(1)} = 1 \\[8pt] q &= -\frac{D}{4a} = - \frac{b^2-4ac}{4a} \\[8pt] &= -\frac{(-2)^2-4(1)(3m-1)}{4(1)} = - \frac{4-12m+4}{4} \\[8pt] &= -\frac{8-12m}{4}= \frac{12m-8}{4} \\[8pt] &= 3m-2 \end{aligned}

Berdasarkan hasil di atas, kita peroleh deret geometri tak hingga berikut:

\begin{aligned} 2p + \frac{q}{4} + \cdots &= 4 \\[8pt] 2 + \frac{3m-2}{4}+\cdots &= 4 \\[8pt] \frac{a}{1-r} = 4 \Leftrightarrow \frac{2}{1-\frac{3m-2}{8}} &= 4 \\[8pt] 4 \times \left( 1-\frac{3m-2}{8} \right) &= 2 \\[8pt] 4-\frac{3m-2}{2} &= 2 \\[8pt] \frac{3m-2}{2} &= 4-2 \\[8pt] 3m-2 &= 4 \\[8pt] m &= 2 \end{aligned}

Jawaban D.

Contoh 9: SBMPTN 2013

Diketahui deret geometri tak hingga \( U_1+U_2+U_3+\cdots \). Jika rasio deret tersebut adalah \(r\) dengan \(-1 < r < 1\) dan \( U_1+U_3+U_5+\cdots = \frac{2}{3}U_1+(U_2+U_4+U_6+\cdots) \) maka nilai \(r^2 = \cdots \)

Pembahasan »

Diketahui \( U_1+U_3+U_5+\cdots = \frac{2}{3}U_1+(U_2+U_4+U_6+\cdots) \) sehingga kita peroleh berikut:

\begin{aligned} U_1+U_3+U_5+\cdots &= \frac{2}{3}U_1+(U_2+U_4+U_6+\cdots) \\[8pt] S_{\text{ganjil}} &= \frac{2}{3}a+S_{\text{genap}} \\[8pt] \frac{a}{1-r^2} &= \frac{2}{3}a+\frac{ar}{1-r^2} \\[8pt] \frac{a}{1-r^2}-\frac{ar}{1-r^2} &= \frac{2}{3}a \\[8pt] \frac{a(1-r)}{(1-r)(1+r)} &= \frac{2}{3}a \\[8pt] \frac{1}{1+r} &= \frac{2}{3} \Leftrightarrow 2+ 2r = 3 \\[8pt] 2r &= 3-2 \Leftrightarrow r = \frac{1}{2} \\[8pt] r^2 &= \left(\frac{1}{2} \right)^2 = \frac{1}{4} \end{aligned}

Jawaban B.

Contoh 10: SBMPTN 2014

Jika \( S=1+\frac{1}{2} \sin 2x + \frac{1}{4} \sin^2 2x + \frac{1}{8} \sin^3 2x + \cdots \) maka...

\( \frac{2}{3} < S < 2 \)
\( \frac{3}{2} < S < 2 \)
\( \frac{2}{3} < S < \frac{3}{2} \)
\( \frac{1}{2} < S < \frac{3}{2} \)
\( \frac{1}{2} < S < \frac{2}{3} \)

Pembahasan »

Ingat bahwa deret tak hingga akan konvergen dengan syarat \( -1 < r < 1 \) sehingga kita peroleh:

\begin{aligned} -1 < r &< 1 \\[8pt] -1 < \frac{1}{2} \sin 2x &< 1 \\[8pt] -2 < \sin 2x &< 2 \end{aligned}

Selanjutnya, berdasarkan jumlah deret tak hingga, maka:

\begin{aligned} S_\infty &= \frac{a}{1-r} = \frac{1}{1-\frac{1}{2} \sin 2x} \\[8pt] &= \frac{2}{2-\sin 2x} \\[8pt] \text{Untuk} \ \sin 2x &= -1, \ \text{maka} \ S_\infty = \frac{2}{2+1} = \frac{2}{3} \\[8pt] \text{Untuk} \ \sin 2x &= 1, \ \text{maka} \ S_\infty = \frac{2}{2-1} = 2 \\[8pt] \text{Jadi,} \ &\frac{2}{3} < S < 2 \end{aligned}

Jawaban A.

Contoh 11:

Jumlah tak hingga dari deret geometri \( 18 + 12 + 8 + \cdots \) adalah…

Pembahasan »

Deret geometri tak hingga pada soal ini memiliki suku pertama \(a = 18\) dan rasio \(r = \frac{U_2}{U_1} = \frac{12}{18}=\frac{2}{3}\). Dengan demikian, jumlah tak hingga deret geometri tersebut adalah sebagai berikut:

\begin{aligned} S_\infty &= \frac{a}{1-r} \\[8pt] &= \frac{18}{1-\frac{2}{3}} = \frac{18}{\frac{1}{3}} \\[8pt] &= 18 \times 3 = 54 \end{aligned}

Jawaban C.

Contoh 12:

Jumlah tak hingga dari deret geometri \( 1-\frac{3}{4}+\frac{9}{16}-\frac{27}{64}+\cdots \) adalah…

\( \frac{3}{7} \)
\( \frac{4}{7} \)
\( \frac{5}{7} \)
\( \frac{6}{7} \)
\( \frac{8}{7} \)

Pembahasan »

Deret geometri tak hingga yang diberikan pada soal mempunyai suku pertama \(a = 1\) dan rasionya \( r= -\frac{3}{4} \). Dengan demikian, jumlah tak hingga deret geometri tersebut sebagai berikut:

\begin{aligned} S_\infty &= \frac{a}{1-r} \\[8pt] &= \frac{1}{1-\left(-\frac{3}{4} \right)} = \frac{1}{\frac{7}{4}} \\[8pt] &= 1 \times \frac{4}{7} = \frac{4}{7} \end{aligned}

Jawaban B.

Contoh 13:

Jumlah suatu deret geometri tak hingga adalah 30 dengan rasio 2/3. Suku pertama deret tersebut adalah…

Pembahasan »

Dari soal diketahui \( S_\infty = 30 \) dan \( r = \frac{2}{3} \). Dengan demikian, suku pertama deret tersebut, yaitu:

\begin{aligned} S_\infty &= \frac{a}{1-r} \\[8pt] 30 &= \frac{a}{1-\frac{2}{3}} \\[8pt] 30 &= \frac{a}{\frac{1}{3}} \\[8pt] a &= 30 \times \frac{1}{3} = 10 \end{aligned}

Jawaban E.

Contoh 14:

Jika jumlah tak hingga deret \( a+a^0 + a^{-1} + a^{-2} + a^{-3} + \cdots \) adalah \(4a\), maka nilai \(a\) adalah…

\( \frac{4}{3} \)
\(2\)
\( \frac{3}{2} \)
\(3\)
\(4\)

Pembahasan »

Deret tak hingga dalam soal di atas memiliki suku pertama sama dengan \(a\), rasionya \(r = \frac{1}{a}\) dan jumlah tak hingga deret tersebut adalah \(4a\). Dengan menggunakan rumus jumlah deret tak hingga, kita peroleh nilai \(a\) sebagai berikut:

\begin{aligned} S_\infty = \frac{a}{1-r} \Leftrightarrow 4a &= \frac{a}{1-\frac{1}{a}} \\[8pt] 4a &= \frac{a}{\frac{a-1}{a}} \\[8pt] 4a &= \frac{a^2}{a-1} \\[8pt] 4a(a-1) &= a^2 \\[8pt] 4a^2-4a &= a^2 \\[8pt] 3a &= 4 \\[8pt] a &= \frac{4}{3} \end{aligned}

Jawaban A.

Contoh 15:

Jika diketahui \( {}^a \! \log b + ( {}^a \! \log b )^2 + ( {}^a \! \log b )^3 + \cdots = 2 \), maka \( {}^a \! \log b + {}^b \! \log \sqrt[3]{a^2} = \cdots \)

\( 1 \)
\( \frac{3}{2} \)
\( \frac{5}{3} \)
\( 2 \)
\( 3 \)

Pembahasan »

Untuk menyelesaikan soal ini ada beberapa sifat logaritma yang perlu kamu pahami terlebih dahulu. Dari deret yang diberikan pada soal, diketahui suku pertama \( U_1 = {}^a \! \log b \) dan rasio deretnya \(r = {}^a \! \log b \) sehingga berlaku:

\begin{aligned} S_\infty = \frac{a}{1-r} \Leftrightarrow S_\infty &= \frac{{}^a \! \log b}{1-{}^a \! \log b} \\[8pt] 2 &= \frac{{}^a \! \log b}{{}^a \! \log a-{}^a \! \log b} \\[8pt] 2 &= \frac{{}^a \! \log b}{{}^a \! \log \frac{a}{b}} \\[8pt] 2 \cdot {}^a \! \log \frac{a}{b} &= {}^a \! \log b \\[8pt] {}^a \! \log \left( \frac{a}{b} \right)^2 &= {}^a \! \log b \\[8pt] \left( \frac{a}{b} \right)^2 &= b \\[8pt] a^2 &= b^3 \\[8pt] b &= a^{\frac{2}{3}} \end{aligned}

Dengan demikian, kita peroleh berikut ini:

\begin{aligned} {}^a \! \log b + {}^b \! \log \sqrt[3]{a^2} &= {}^a \! \log a^{\frac{2}{3}} + {}^b \! \log \sqrt[3]{b^3} \\[8pt] &= \frac{2}{3} \cdot {}^a \! \log a + {}^b \! \log b \\[8pt] &= \frac{2}{3} \cdot 1 + 1 \\[8pt] &= \frac{5}{3} \end{aligned}

Jawaban C.

Contoh 16: UNBK Matematika SMA IPS 2019

Jumlah tak hingga dari deret \( 4 + 3 + \frac{9}{4} + \frac{27}{16} + \frac{81}{64} + \cdots \) adalah…

\( \frac{13}{3} \)
\( \frac{16}{3} \)
\( 13 \)
\( 16 \)
\( \frac{65}{4} \)

Pembahasan »

Dari deret yang diberikan pada soal diketahui \(a = 4\) dan rasio \( r = \frac{U_2}{U_1} = \frac{3}{4} \). Dengan demikian, jumlah tak hingga deret tersebut adalah sebagai berikut:

\begin{aligned} S_\infty &= \frac{a}{1-r} \\[8pt] &= \frac{4}{1-\frac{3}{4}} = \frac{4}{\frac{1}{4}} \\[8pt] &= 4 \times 4 = 16 \end{aligned}

Jawaban D.

Contoh 17: UMPTN 2001

Diketahui deret geometri tak hingga \(16+4+1+\cdots\). Jika jumlah deret tersebut dikurangi dengan jumlah \(n\) suku pertama, hasilnya kurang dari \( \frac{1}{3.000} \). Nilai \(n\) terkeccil yang memenuhi adalah…

Pembahasan »

Dari deret \(16+4+1+\cdots\) diketahui suku pertama \(a=16\) dan rasio \(r = \frac{1}{4}\), sehingga diperoleh:

\begin{aligned} S_\infty - S_n < \frac{1}{3.000} \\[8pt] \frac{a}{1-r}-\frac{a(1-r^n)}{1-r} < \frac{1}{3.000} \\[8pt] \frac{16}{1-\frac{1}{4}}-\frac{16\left(1-(\frac{1}{4})^n \right)}{1-\frac{1}{4}} < \frac{1}{3.000} \\[8pt] \frac{16}{\frac{3}{4}}-\frac{16-16 \left( \frac{1}{4} \right)^n}{\frac{3}{4}} < \frac{1}{3.000} \\[8pt] 16-16-16 \left( \frac{1}{4} \right)^n < \frac{1}{4.000} \\[8pt] 16 \left( \frac{1}{4} \right)^n < \frac{1}{4.000} \\[8pt] \left( \frac{1}{4} \right)^{-2} \cdot \left( \frac{1}{4} \right)^n < \frac{1}{250} \cdot \left( \frac{1}{4} \right)^2 \\[8pt] \left( \frac{1}{4} \right)^{-4} \cdot \left( \frac{1}{4} \right)^n < \frac{1}{250} \\[8pt] \left( \frac{1}{4} \right)^{n-4} < \frac{1}{250} \end{aligned}

Perhatikan bahwa \( \left( \frac{1}{4} \right)^4 = \frac{1}{256} \) sehingga nilai \(n\) terkecil agar \( \left( \frac{1}{4} \right)^{n-4} < \frac{1}{250} \) adalah \( n-4=4 \) atau \(n = 8 \).

Jawaban D.

Contoh 18: SBMPTN 2013

Parabola \( y = x^2-2x+m+2 \) mempunyai titik puncak \( (p,q) \). Jika \(3p\) dan \(q\) dua suku pertama deret geometri tak hingga yang mempunyai jumlah 9, maka nilai \(m\) adalah…

-3
-1
1
2
3

Pembahasan »

Untuk menyelesaikan soal ini kita perlu mengetahui rumus titik puncak fungsi kuadrat yaitu \( \left( -\frac{b}{2a}, - \frac{D}{4a} \right) \) dan rumus jumlah deret geometri tak hingga yaitu: \( S_\infty = \frac{a}{1-r} \).

Dari soal diketahui parabola \( y = x^2-2x+m+2 \), sehingga diperoleh:

\begin{aligned} p &= -\frac{b}{2a} = - \frac{-2}{2(1)} = 1 \\[8pt] q &= - \frac{D}{4a} = -\frac{b^2-4ac}{4a} \\[8pt] &= -\frac{(-2)^2-4(1)(m+2)}{4(1)} \\[8pt] &= - \frac{4-4m-8}{4} = -\frac{-4-4m}{4} \\[8pt] &= 1+m \end{aligned}

Berdasarkan hasil di atas, maka diperoleh deret geometri tak hingga, yaitu:

\begin{aligned} 3+(1+m)+\cdots &= 9 \\[8pt] \frac{a}{1-r} &= 9 \Leftrightarrow \frac{3}{1-\frac{1+m}{3}} = 9 \\[8pt] 3 &= 9 \times \left( 1-\frac{1+m}{3} \right) \\[8pt] 3 &= 9-3(1+m) \\[8pt] 3 &= 6-3m \\[8pt] 3m &= 3 \\[8pt] m &= 1 \end{aligned}

Jawaban C.

Contoh 19:

Jumlah deret geometri tak hingga \( 27-9+3-1+\frac{1}{3}+ \cdots \) adalah…

\( \frac{27}{2} \)
\( \frac{27}{4} \)
\( \frac{81}{2} \)
\( \frac{81}{4} \)
\( -\frac{81}{4} \)

Pembahasan »

Deret geometri tak hingga dalam soal ini memiliki suku pertama \(a=27\) dan rasio \(r = \frac{-9}{27} = -\frac{1}{3}\). Dengan demikian, jumlah tak hingga deret geometri tersebut adalah sebagai berikut:

\begin{aligned} S_\infty &= \frac{a}{1-r} \\[8pt] &= \frac{27}{1-\left(-\frac{1}{3} \right)} = \frac{27}{\frac{4}{3}} \\[8pt] &= 27 \times \frac{3}{4} = \frac{81}{4} \end{aligned}

Jawaban D.

Contoh 20: UN 2015

Sebuah bola dijatuhkan dari ketinggian \(5 \ m\) dan memantul kembali dengan \( \frac{3}{5} \) kali tinggi sebelumnya. Panjang lintasan gerak bola sampai berhenti adalah…

\( \frac{15}{2} \ m \)
\( \frac{25}{2} \ m \)
\( 15 \ m \)
\( 20 \ m \)
\( 25 \ m \)

Pembahasan »

Kita dapat menggunakan konsep deret geometri tak hingga untuk menghitung panjang lintasan gerak bola sampai berhenti.

Dari soal diketahui bahwa tinggi bola awal adalah \(5 \ m\) dan memantul kembali dengan ketinggian \( \frac{3}{5} \) dari \(5 \ m\) yaitu \(3 \ m \). Selanjutnya, bola kembali turun setinggi \(3 \ m\) dan memantul kembali setinggi \( \frac{3}{5} \) dari \( 3 \ m \) yaitu \( \frac{9}{5} \ m\). Lalu bola turun lagi setinggi \( \frac{9}{5} \ m \) dan memantul kembali setinggi \( \frac{3}{5} \) dari \( \frac{9}{5} \ m \) yaitu \( \frac{27}{25} \ m \), begitu seterusnya sampai bola berhenti.

Dari hasil di atas diperoleh bahwa tinggi bola pertama disebut sebagai suku pertama yakni \(a = 5\) dan rasionya yaitu \( r = \frac{3}{5} \). Dengan demikian, panjang lintasan bola sampai bola berhenti dapat dihitung sebagai berikut:

\begin{aligned} \text{Panjang lintasan} &= (S_\infty \times 2) - 5 \\[8pt] \text{Panjang lintasan} &= \left( \frac{a}{1-r} \times 2 \right) - 5 \\[8pt] &= \left( \frac{5}{1-\frac{3}{5}} \times 2 \right)-5 \\[8pt] &= \left( \frac{25}{2} \times 2\right) - 5 \\[8pt] &= 20 \end{aligned}

Perhatikan bahwa kita mengalikan \( S_{\infty} = \frac{a}{1-r} \) dengan 2 lalu dikurang 5, karena lintasan bola yang \(5 \ m\) hanya terjadi satu kali.

Jawaban D.

Contoh 21: SIMAK UI 2017

Nilai \(x\) yang memenuhi \( 1 + (x-1)^2+(x-1)^3+(x-1)^4 + \cdots = 2-x \) adalah…

\( \frac{-3+\sqrt{3}}{2} \)
\( 0 \)
\( \frac{3-\sqrt{3}}{2} \)
\(1\)
\( \frac{3+\sqrt{3}}{2} \)

Pembahasan »

Perhatikan bahwa deret yang diberikan dalam soal dapat kita manipulasi menjadi:

\begin{aligned} &\Leftrightarrow 1 + (x-1)^2+(x-1)^3+(x-1)^4 + \cdots = 2-x \\[8pt] &\Leftrightarrow (x-1)^2+(x-1)^3+(x-1)^4 + \cdots = 2-x-1 \\[8pt] &\Leftrightarrow (x-1)^2+(x-1)^3+(x-1)^4 + \cdots = 1-x \end{aligned}

Deret yang telah dimanipulasi di atas adalah deret geometri tak hingga dengan \( a = (x-1)^2 \) dan \( r = (x-1) \). Dengan demikian, berdasarkan deret geometri tak hingga, kita peroleh berikut ini:

\begin{aligned} S_\infty &= \frac{a}{1-r} \\[8pt] 1- x &= \frac{(x-1)^2}{1-(x-1)} \\[8pt] 1-x &= \frac{x^2-2x+1}{2-x} \\[8pt] (1-x)(2-x) &= x^2-2x+1 \\[8pt] x^2-3x+2 &= x^2-2x+1 \\[8pt] x^2-x^2-3x+2x &= 1-2 \\[8pt] -x &= -1 \\[8pt] x &= 1 \end{aligned}

Jawaban D.

Contoh 22: UM UGM 2007

Jika \(x-1, x-\frac{3}{2}, x-\frac{7}{4}\) adalah tiga suku pertama deret geometri, maka jumlah tak hingga deret tersebut adalah…

\( -2 \)
\( -1 \)
\( -\frac{1}{2} \)
\(1\)
\( 2 \)

Pembahasan »

Dari deret geometri yang diberikan, kita peroleh hubungan berikut:

\begin{aligned} \left( x-\frac{3}{2} \right)^2 &= (x-1) \left( x-\frac{7}{4} \right) \\[8pt] x^2-3x+\frac{9}{4} &= x^2-\frac{11}{4}x+\frac{7}{4} \\[8pt] -3x+\frac{9}{4} &= -\frac{11}{4}x+\frac{7}{4} \\[8pt] -3x + \frac{11}{4}x &= \frac{7}{4}- \frac{9}{4} \\[8pt] -\frac{1}{4}x &= -\frac{2}{4} \\[8pt] x &= 2 \end{aligned}

Barisan geometri dan jumlah tak hingga deret tersebut yaitu:

\begin{aligned} a = U_1 = x-1 &= 2-1 = 1 \\[8pt] U_2 = x-\frac{3}{2} &= 2-\frac{3}{2} = \frac{1}{2} \\[8pt] U_3 = x-\frac{7}{4} &= 2-\frac{7}{4} = \frac{1}{4} \\[8pt] r &= \frac{U_n}{U_{n-1}} = \frac{U_2}{U_1} = \frac{\frac{1}{2}}{1} = 1 \\[8pt] S_\infty &= \frac{a}{1-r} = \frac{1}{1-\frac{1}{2}} \\[8pt] &= \frac{1}{\frac{1}{2}} = 2 \end{aligned}

Jawaban E.

Contoh 23: SPMB 2006

Jumlah suatu deret geometri tak hingga dengan suku pertama \( a \) dan rasio \(r\) dengan \( 0 < r < 1\) adalah \(S\). Jika suku pertama tetap dan rasio berubah menjadi \(1-r\), maka jumlahnya menjadi…

\( S \left( 1-\frac{1}{r} \right) \)
\( \frac{S}{r} \)
\( S \left( \frac{1}{r}+r \right) \)
\( \frac{S}{1-r} \)
\( S \left( \frac{1}{r}-1 \right) \)

Pembahasan »

Untuk jumlah deret geometri tak hingga dengan suku pertama \(a\) dan rasio \(r\), kita peroleh berikut ini:

\begin{aligned} S_\infty = \frac{a}{1-r} \Leftrightarrow S &=\frac{a}{1-r} \\[8pt] \Leftrightarrow a &= S(1-r) \end{aligned}

Dari hasil di atas, kita peroleh nilai \(a\) sama dengan \(S(1-r)\). Dengan demikian, kita peroleh jumlah deret geometri tak hingga dengan suku pertama \(a\) dan rasio \(1-r\) yaitu sebagai berikut:

\begin{aligned} S_\infty = \frac{a}{1-r} \Leftrightarrow S_\infty &=\frac{S(1-r)}{1-(1-r)} \\[8pt] &= \frac{S(1-r)}{r} = S \left( \frac{1}{r}-\frac{r}{r} \right) \\[8pt] &= S \left( \frac{1}{r}-1 \right) \end{aligned}

Jawaban E.

Contoh 24: SPMB 2005

Jika suku ke-\(n\) suatu deret adalah \( U_n = 2^{2x-n} \), maka jumlah tak hingga deret tersebut adalah…

\( 2^{2x-2} \)
\( 2^{2x-1} \)
\( 2^{2x} \)
\( 2^{2x+1} \)
\( 2^{2x+2} \)

Pembahasan »

Karena \( U_n = 2^{2x-n} \), maka deret geometri yaitu \( 2^{2x-1}, 2^{2x-2}, 2^{2x-2}, \cdots \). Dari deret tersebut terlihat bahwa suku pertama \(a = 2^{2x-1} \) dan rasionya \( r = \frac{1}{2}\). Dengan demikian, kita peroleh berikut ini:

\begin{aligned} S_\infty &= \frac{a}{1-r} = \frac{2^{2x-1}}{1-\frac{1}{2}} \\[8pt] &= \frac{2^{2x-1}}{\frac{1}{2}} = \frac{2^{2x-1}}{2^{-1}} \\[8pt] &= 2^{2x-1-(-1)} \\[8pt] &= 2^{2x} \end{aligned}

Jawaban C.

Contoh 25: SPMB 2005

Agar deret geometri tak hingga dengan suku pertama \(a\) mempunyai jumlah 2, maka \(a\) mempunyai….

\( -2 < a < 0 \)
\( -4 < a < 0 \)
\( 0 < a < 2 \)
\( 0 < a < 4 \)
\( -4 < a < 4 \)

Pembahasan »

Diketahui deret geometri tak hingga dengan jumlah 2, sehingga berlaku:

\begin{aligned} S_\infty = \frac{a}{1-r} \Leftrightarrow 2 &= \frac{a}{1-r} \\[8pt] 2(1-r) &= a \\[8pt] 2-2r &= a \\[8pt] 2r &= 2-a \\[8pt] r &= \frac{2-a}{2} \end{aligned}

Ingat bahwa syarat agar deret geometri tak hingga mempunyai jumlah 2 adalah rasionya terbatas pada \( -r < r < 1 \). Berdasarkan batasan rasio ini, kita peroleh berikut ini:

\begin{aligned} -1 < r &< 1 \\[8pt] -1 < \frac{2-a}{2} &< 1 \\[8pt] -2 < 2-a &< 2 \\[8pt] -2 + 2 < 2-a+2 &< 2+2 \\[8pt] 0 < a &< 4 \end{aligned}

Jawaban D.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.

www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

Matematika Dasar » Barisan dan Deret › Barisan dan deret tak hingga: Rumus, contoh soal dan pembahasan