
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Limit Fungsi › Limit Tak Hingga - Materi, Contoh Soal dan Pembahasan
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Limit Tak Hingga - Materi, Contoh Soal dan Pembahasan
Dengan konsep limit tak hingga, kita dapat mengetahui kecenderungan suatu fungsi jika nilai peubahnya bertambah besar tanpa batas atau \(x\) menuju tak hingga, \((x → ∞)\).
Pada artikel sebelumnya kita telah belajar mengenai definisi limit dan limit fungsi aljabar. Pada artikel tersebut kita hanya mempelajari limit di mana nilai \(x\) mendekati suatu bilangan yang berhingga baik positif maupun negatif. Misalnya, \( \lim_\limits{x\to 2} f(x) \) atau lebih umumnya \( \lim_\limits{x\to c} f(x) \) di mana \(c\) suatu bilangan yang berhingga.
Namun, tak jarang kita akan menjumpai limit di mana nilai \(x\) mendekati tak hingga yakni \( \lim_\limits{x\to\infty} f(x) \). Dengan konsep limit tak hingga ini, kita dapat mengetahui kecenderungan suatu fungsi jika nilai variabel atau peubahnya dibuat semakin besar atau bertambah besar tanpa batas atau \(x\) menuju tak hingga, dinotasikan dengan \( x \to \infty \).
Misalkan terdapat fungsi \( f(x) = \frac{1}{x^2} \). Bayangkan apa yang terjadi dengan fungsi \(f(x)\) jika \(x\) bertambah semakin besar? Untuk menjawab ini, amati nilai fungsi \(f(x)\) untuk nilai-nilai \(x\) berikut.

Dari ilustrasi di atas dapat kita lihat bahwa fungsi \(f(x)\) semakin mendekati nol ketika \(x\) semakin besar. Grafik dari fungsi tersebut dapat dilihat pada Gambar 1 di bawah.

Gambar 1. Kurva \( y = 1/x^2 \)
Dari Gambar 1 terlihat bahwa kurva \( y = \frac{1}{x^2} \) semakin mendekati garis \(y = 0\) ketika \(x\) semakin besar. Secara intuitif, kita simpulkan bahwa jika \(x\) semakin besar tanpa batas maka nilai \( 1/x^2 \) semakin dekat ke nol. Dalam notasi limit, pernyataan ini ditulis

Dengan demikian, kita peroleh sifat berikut ini.
Sifat A:
Jika \(n > 0\) dan \(n\) bilangan rasional, maka

Baca juga:
Tentu saja, untuk mengetahui nilai suatu fungsi \(f(x)\) ketika \(x\) bertambah besar dengan mengambil beberapa nilai dan menghitung nilai fungsi tersebut lalu menggambarkannya pada grafik, bukan cara yang efisien. Dalam beberapa kasus, hal tersebut sulit atau bahkan tak dapat dilakukan. Sebagai contoh, perhatikan limit-limit berikut.

Bagaimanakah bentuk grafik pada kedua limit di atas? Tentu saja, cukup sulit untuk mendapatkan grafik fungsi tersebut. Oleh karena itu, kita perlu cara lain untuk mengetahui kecenderungan nilai fungsi tersebut ketika \(x\) bertambah besar.
Sebenarnya, kita dapat gunakan cara substitusi langsung, jika hasil yang diperoleh bukan dalam bentuk tak tentu (0/0, \( ∞/∞ \), \( ∞-∞ \), dan bentuk tak tentu lainnya). Namun, jika hasil yang diperoleh adalah bentuk tak tentu maka kita gunakan metode lain.
Contoh 1:
Hitung \( \lim_\limits{x \to \infty } \, \left ( x^{3}-7x^{2} \right) \).
Pembahasan:
Jika kita gunakan metode substitusi langsung untuk menyelesaikan limit ini, maka akan diperoleh bentuk tak tentu \( \infty - \infty \). Namun, kita masih dapat gunakan metode substitusi langsung dengan terlebih dahulu mengubah fungsi dalam limitnya supaya tidak berbentuk tak tentu ketika nilai variabelnya disubstitusikan ke fungsi dalam limit. Perhatikan berikut ini.

Perhatikan bahwa pada Contoh 1 kita menggunakan substitusi langsung karena hasil yang diberikan bukan dalam bentuk tak tentu. Karena kita tidak selalu dapat menggunakan metode substitusi, maka kita akan mempelajari metode lain untuk mencari limit tak hingga.
Terdapat dua metode yang akan kita pelajari yakni metode membagi dengan pangkat tertinggi dan metode mengalikan bentuk sekawan.
Metode Pembagian dengan Pangkat Tertinggi
Metode ini diterapkan pada limit dengan fungsi berbentuk \( \lim_\limits{x\to∞} \frac{f(x)}{g(x)} \). Metode ini dapat dikerjakan dengan membagi fungsi pada pembilang \(f(x)\) dan fungsi pada penyebut \(g(x)\) dengan peubah \(x^n\) berpangkat tertinggi yang ada dalam fungsi \(f(x)\) dan \(g(x)\). Lalu, lakukan penyederhanaan fungsi pada limit dan setelah itu baru disubstitusi dengan \( x \to ∞ \).
Perhatikan beberapa contoh berikut.
Contoh 2:
Tentukan nilai dari \( \displaystyle \lim_\limits{x \to \infty }\,\frac{x^{3}-4x}{3x^{3}+x^{2}} \).
Pembahasan:
Perhatikan fungsi yang ada dalam limit. Variabel dengan pangkat tertinggi dari pembilang adalah \(x^3\). Begitu pula dengan penyebutnya. Jadi, variabel dengan pangkat tertinggi antara pembilang dan penyebutnya adalah \(x^3\).
Selanjutnya, bagi pembilang dan penyebut dengan variabel pangkat tertinggi yang telah diperoleh, yaitu \(x^3\), kemudian hitung limit dari masing-masing suku dengan berpedoman pada sifat A yang telah kita bahas sebelumnya.

Jadi, kita peroleh nilai limit sama dengan 1/3.
Contoh 3:
Hitung nilai dari \( \displaystyle \lim_\limits{x \to \infty }\,\frac{x^{3}-x}{x^{4}-2x^{2}+1} \).
Pembahasan:
Perhatikan bahwa variabel dengan pangkat tertinggi dalam soal ini yaitu \(x^4\). Jadi, bagi pembilang dan penyebut dari fungsi limitnya dengan variabel pangkat tertinggi, yaitu \(x^4\), kemudian hitung limitnya.

Jadi, kita peroleh nilai limit sama dengan 0.
Contoh 4:
Hitung nilai dari \( \displaystyle \lim_\limits{x \to \infty }\,\frac{x-x^{3}}{x^{2}-4} \).
Pembahasan:
Bagi pembilang dan penyebut dengan variabel pangkat tertinggi dari pembilang, yaitu \(x^3\), kemudian hitung limitnya.
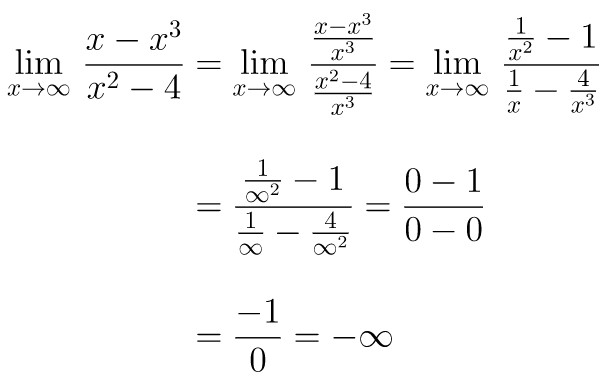
Jadi, kita peroleh nilai limit sama dengan \( -\infty \).
Catatan: Perhatikan bahwa di sini kita bisa melakukan pembagian dengan nol, karena kita sedang berbicara tentang limit, sehingga nilai nol yang dimaksud di sini tidak mutlak nol, melainkan 'mendekati nol'. Jadi, maksud dari (-1/0) di atas adalah -1 dibagi dengan angka yang amat sangat kecil yang mendekati nol (misalnya: 0,00000000000001) sehingga diperoleh jawaban \(-\infty\).
Jika kita sedang tidak berbicara tentang limit, maka kita tahu pembagian dengan nol adalah tidak terdefinisi.
Terdapat sifat yang berguna terkait metode pembagian dengan pangkat tertinggi ini. Kita cantumkan sebagai berikut.
Sifat B:
Jika \(p(x)\) dan \(q(x)\) adalah fungsi polinom dengan \(ax^m\) dan \(bx^n\) berturut-turut adalah suku pangkat tertinggi dari \(p(x)\) dan \(q(x)\), maka

Sifat di atas mengatakan bahwa nilai limit tak hingga untuk fungsi polinom ataupun rasional sama dengan nilai limit dari suku pangkat tertingginya. Dengan menggunakan sifat di atas, contoh 1 dan 2 dapat diselesaikan dengan cara sebagai berikut.

Berdasarkan pangkat tertinggi pembilang dan penyebutnya, sifat B poin 3 dapat kita jabarkan lagi menjadi sebagai berikut.
Sifat C:
Misalkan \(p(x)\) dan \(q(x)\) adalah fungsi polinom dengan \(ax^m\) dan \(bx^n\) berturut-turut adalah suku pangkat tertinggi dari \(p(x)\) dan \(q(x)\), maka
- Jika \(m = n \), maka
- Jika \(m < n \), maka
- Jika \(m > n \), maka



Sifat di atas dapat kita terjemahkan dalam tiga poin berikut.
- Jika pangkat tertinggi pembilang = pangkat tertinggi penyebut, nilai limitnya adalah koefisien pangkat tertinggi pembilang dibagi koefisien pangkat tertinggi penyebut.
- Jika pangkat tertinggi pembilang < pangkat tertinggi penyebut, nilai limitnya = 0.
- Jika pangkat tertinggi pembilang > pangkat tertinggi penyebut, nilai limitnya = ∞ (asalkan perbandingan koefisiennya positif) atau -∞ (asalkan perbandingan koefisiennya negatif)
Dengan menggunakan sifat C; Contoh 2, 3, dan 4 dapat diselesaikan cukup dengan memperhatikan suku pangkat tertinggi dari pembilang dan penyebut, dalam hal ini adalah pangkat dan koefisiennya.
Dalam Contoh 2, pangkat tertinggi pembilang sama dengan pangkat tertinggi penyebut sehingga berdasarkan Sifat C poin 1, nilai limitnya adalah koefisien pangkat tertinggi pembilang dibagi koefisien pangkat tertinggi penyebut, yaitu 1/3.

Pada Contoh 3, pangkat tertinggi pembilang < pangkat tertinggi penyebut sehingga berdasarkan Sifat C poin 2, nilai limitnya = 0.

Pada Contoh 4, pangkat tertinggi pembilang > pangkat tertinggi penyebut dan perbandingan koefisiennya negatif sehingga berdasarkan Sifat C poin 3, nilai limitnya = -∞.

Metode Perkalian dengan Bentuk Sekawan
Metode ini diterapkan pada limit yang berbentuk \( \lim_\limits{x\to∞} (f(x)-g(x)) \). Untuk menyelesaikan limit dengan bentuk demikian, kita mengalikan dengan bentuk sekawannya. Perhatikan contoh berikut.
Contoh 5:
Tentukan nilai dari \( \lim_\limits{x \to \infty } \left( 2x-\sqrt{4x^{2}+x} \right) \).
Pembahasan:
Lakukan analisa sederhana untuk memeriksa apakah limit tersebut merupakan bentuk tak tentu.
Perhatikan bahwa jika \(x \rightarrow \infty\) maka \(2x\rightarrow \infty\) dan \(\sqrt{4x^{2}+x}\rightarrow \infty\). Akibatnya,

Dengan demikian, kita tidak dapat gunakan metode substitusi. Kita gunakan metode perkalian dengan bentuk sekawan, yakni

Contoh 6:
Hitunglah nilai dari \( \lim_\limits{x \to -\infty }\left ( \sqrt{x^{2}-2x}\;-4x \right ) \).
Pembahasan:
Jangan terburu-buru mengalikan bentuk diatas dengan akar sekawannya. Lakukan analisa sederhana untuk memeriksa apakah limit tersebut merupakan bentuk tak tentu.
Jika \(x\rightarrow -\infty\) maka \(\sqrt{x^{2}-2x}\rightarrow \infty\) dan \(4x\rightarrow -\infty\). Akibatnya,

Karena cara substitusi di atas tidak menghasilkan bentuk tak tentu, maka kita tidak perlu menggunakan metode perkalian akar sekawan. Dengan demikian,
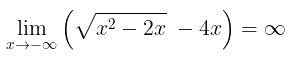
Contoh 7:
Tentukan nilai dari \( \lim_\limits{x \to \infty } \sqrt{1 + x} - \sqrt{x} \).
Pembahasan:
Dengan cara substitusi langsung akan diperoleh bentuk tak tentu \( \infty-\infty \) sehingga kita gunakan metode perkalian akar sekawan. Berikut hasil yang diperoleh:

Terdapat teorema yang penting terkait dengan perkalian bentuk sekawan yang perlu Anda ketahui. Kita cantumkan sebagai berikut.
Teorema:
Jika \(a = p\) dan \(a, p ≠ 0\) maka
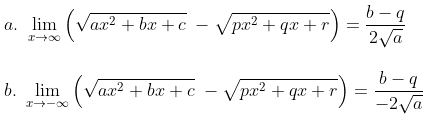
Bukti: (a)
Untuk \(a = p\), bentuk pada poin a teorema di atas dapat diubah menjadi

Kalikan dengan akar sekawannya lalu sederhanakan sehingga diperoleh

Bukti: (b)
Untuk \(a = p\), bentuk pada poin b teorema di atas dapat diubah menjadi

Kalikan dengan akar sekawannya lalu sederhanakan sehingga diperoleh

Perlu kita ingat bahwa untuk \(x → -∞\) maka \( \sqrt{x^2} = -x \). Akibatnya, hasil yang kita peroleh di atas menjadi

Contoh 8:
Hitung limit berikut dengan menggunakan teorema yang telah diberikan di atas.
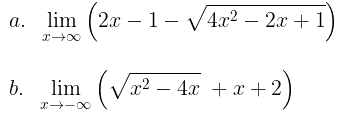
Pembahasan:
Kita akan menghitung limit dari suku konstan secara terpisah dan hitung limit dari suku lainnya menggunakan teorema yang diberikan di atas, dengan terlebih dahulu menyatakannya dalam bentuk akar.


Baca juga:
Teorema-teorema untuk Limit Tak Hingga
Untuk limit limit tak hingga, terdapat beberapa teorema yang perlu diperhatikan. Jika \(n\) adalah bilangan bulat, \(k\) konstanta, fungsi \(f\) dan fungsi \(g\) adalah fungsi-fungsi yang memiliki nilai limit yang mendekati bilangan c, maka:

Contoh-contoh Soal
Berikut ini kita akan membahas lebih banyak contoh soal terkait limit tak hingga.
Contoh 9:
Untuk n bilangan asli dan \(a_0 ≠ 0\), tunjukkan bahwa

Pembahasan:

Contoh 10:
Hitunglah limit berikut.
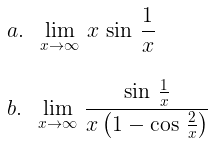
Pembahasan:
- Misalkan \( u = \frac{1}{x} \), maka \( x = \frac{1}{u} \). Jika \( x \to \infty \), maka \( u \to 0 \). Akibatnya,
- Misalkan \( u = \frac{1}{x} \), maka \( x = \frac{1}{u} \). Jika \( x \to \infty \), maka \( u \to 0 \). Akibatnya,

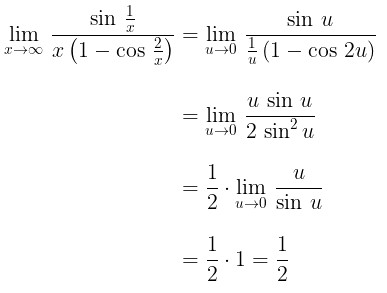
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Life without love is like a tree without blossoms or fruit.
