www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Matriks › Definisi, Notasi, dan Operasi Matriks
Definisi, Notasi, dan Operasi Matriks
Matriks adalah susunan segi empat siku-siku dari bilangan-bilangan. Bilangan-bilangan dalam susunan tersebut dinamakan entri atau elemen dalam matriks.
Dalam matematika, matriks dapat didefinisikan sebagai susunan segi empat siku-siku dari bilangan-bilangan. Bilangan-bilangan dalam susunan tersebut dinamakan entri atau elemen dalam matriks.
Sebagai contoh, susunan berikut adalah matriks.
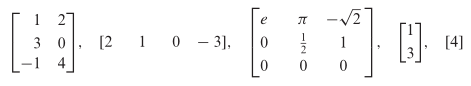
Matriks-matriks yang diberikan dalam contoh ini mempunyai ukuran yang berbeda-beda. Ukuran matriks dinyatakan menurut banyaknya baris (garis horisontal) dan banyaknya kolom (garis vertikal) yang terdapat dalam matriks tersebut. Misalnya, matriks yang pertama dalam contoh ini mempunyai 3 baris dan 2 kolom sehingga ukurannya adalah 3 kali 2 (yang dituliskan \(3 × 2\)).
Angka pertama selalu menunjukkan banyaknya baris dan angka kedua menunjukkan banyaknya kolom. Jadi, matriks lainnya dalam Contoh ini berturut-turut mempunyai ukuran \(1×4, 3×3, 2×1\), dan \(1×1\). Matriks terakhir dalam Contoh ini berukuran \(1×1\), dan biasanya kita hanya menuliskan 4 saja ketimbang [4] dan cara penulisan ini merupakan praktek yang sudah umum.
Dalam penulisan matriks, kita akan menggunakan huruf-huruf besar untuk menyatakan matriks-matriks dan menggunakan huruf-huruf kecil untuk menyatakan elemen-elemen atau entri-entri yang ada pada sebuah matriks; jadi, kita dapat menuliskan

Operasi Matriks
Sama halnya dengan bilangan yang dapat ditambahkan, dikurangkan, dan dikalikan untuk menghasilkan bilangan yang baru, demikian pula dengan matriks yang mana juga bisa ditambahkan, dikurangkan, dan dikalikan untuk menghasilkan suatu matriks baru.
#1. Penjumlahan matriks
Jika \(A\) dan \(B\) adalah sebarang dua matriks yang ukurannya sama, maka jumlah \(A + B\) adalah matriks yang diperoleh dengan menambahkan bersama-sama entri atau elemen yang bersesuain dalam kedua matriks tersebut.
Perhatikan contoh soal berikut:
Contoh 1:
Seorang pedagang buah memiliki 2 toko di lokasi yang berbeda. Pedagang tersebut mendata jumlah buah yang terjual setiap bulannya. Banyak buah yang terjual dapat dilihat pada tabel berikut.
Tabel 1. Jumlah buah yang terjual di dua toko

Berapakah total masing-masing buah yang terjual pada masing-masing toko?
Pembahasan:
Data dalam tabel dapat dibentuk mejadi tiga matriks yang berbeda, yaitu:
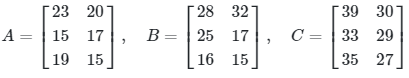
Total masing-masing buah yang terjual pada masing-masing toko adalah

Jadi, toko 1 telah menjual 90 nanas, 73 semangka, dan 70 melon, sedangkan toko 2 telah menjual 82 nanas, 63 semangka, dan 57 melon.
#2. Pengurangan matriks
Jika \(A\) dan \(B\) adalah sebarang dua matriks yang ukurannya sama, maka pengurangan \(A – B\) adalah matriks yang diperoleh dengan melakukan pengurangan bersama-sama entri atau elemen yang bersesuaian dalam kedua matriks tersebut.
Perhatikan contoh soal berikut:
Contoh 2:
Pak Andi mempunyai dua toko pakaian yang menjual pakaian anak dan pakaian dewasa. Di antara stok pakaian yang dikirim oleh pemasok pakaian terdapat stok yang tidak layak jual. Data stok pakaian terdapat di tabel berikut.
Tabel 2. Stok pakaian yang dijual di dua toko
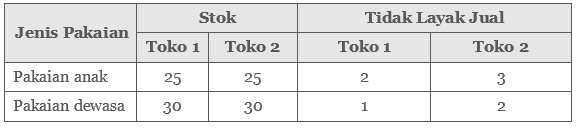
Hitunglah jumlah stok pakaian yang dapat dijual oleh masing-masing toko!
Pembahasan:
Data dalam tabel dapat dibentuk menjadi dua matriks yang berbeda, yaitu

Total jumlah stok pakaian yang dapat dijual oleh masing-masing toko adalah
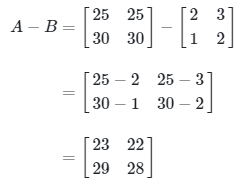
Jadi, toko 1 dapat menjual 23 pakaian anak dan 19 pakaian dewasa, sedangkan toko 2 dapat menjual 22 pakaian anak dan 28 pakaian dewasa.
#3. Perkalian skalar pada matriks
Jika \(A\) adalah suatu matriks dan \(c\) adalah suatu skalar, maka hasil kali (product) \(cA\) adalah matriks yang diperoleh dengan mengalikan masing-masing entri dari \(A\) oleh \(c\).
Perhatikan contoh soal berikut:
Contoh 3:
Sebuah perusahaan pembuat mainan mengirim 3 jenis mainan ke dua toko mainan yang berbeda dengan jumlah yang sama setiap minggunya. Banyaknya mainan yang dikirim setiap minggu disajikan pada Tabel di bawah ini.
Tabel 3. Jumlah mainan yang dikirim

Tentukan total mainan yang dikirim oleh pemasok mainan selama 5 minggu!
Pembahasan:
Data dalam tabel dapat dibentuk menjadi sebuah matriks, yaitu

Maka total mainan yang dikirim selama 5 minggu adalah

Jadi, di toko 1 ada 150 mainan jenis A, 175 mainan jenis B, dan 200 mainan jenis C. Sedangkan di toko 2 ada 175 mainan jenis A, 200 mainan jenis B, dan 275 mainan jenis C.
#4. Perkalian matriks
Misalkan terdapat dua matriks sembarang yakni matriks A yang berukuran 3 x 2 dan matriks B yang berukuran 2 x 3.

Maka perkalian matriks AB didefinisikan sebagai

Perhatikan bahwa matriks AB yang diperoleh adalah berukuran 3 x 3.
Anda harus berhati-hati mengenai perkalian matriks. Tidak semua matriks dapat dilakukan operasi perkalian. Perkalian matriks dapat dilakukan jika banyaknya kolom dari faktor pertama \(A\) harus sama dengan banyaknya baris dari faktor kedua \(B\) supaya membentuk hasil kali \(AB\). Jika kondisi ini tidak dipenuhi, maka hasil kali tersebut tidak dapat didefinisikan.
Sebuah cara yang memudahkan untuk menentukan apakah hasil kali dua matriks dapat didefinisikan adalah dengan menulis ukuran faktor pertama, dan ke sebelah kanannya, kita menuliskan ukuran faktor kedua.
Seperti dalam ilustrasi berikut. Jika bilangan-bilangan yang di sebelah dalam (inside) adalah sama, maka hasil kalinya dapat didefinisikan. Bilangan-bilangan yang di sebelah luar (outside) akan memberikan ukuran hasil kali tersebut.

Perhatikan contoh soal berikut:
Contoh 4:
Adi membeli 2 buku tulis dan 2 pulpen, sedangkan Budi membeli 3 buku dan 2 pulpen. Harga satu buku tulis adalah Rp 5.000,00 dan harga satu pulpen adalah Rp 2.500,00. Berapakah uang yang dikeluarkan oleh Adi dan Budi?
Pembahasan:
Pernyataan Adi membeli 2 buku tulis dan 3 pulpen serta Budi membeli 4 buku dan 1 pulpen dapat dibuat matriks \( \left[ {\begin{array}{cc} 2 & 3 \\ 4 & 1 \\ \end{array} } \right] \), sedangkan harga buku tulis dan pulpen dapat dibuat matriks \( \left[ {\begin{array}{cc} 5.000 \\ 2.500 \\ \end{array} } \right] \)
Sehingga uang yang dikeluarkan oleh Adi dan Budi adalah

Jadi, Adi mengeluarkan uang sebesar Rp 17.500,00 dan Budi mengeluarkan uang sebesar Rp 22.500,00.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
If you live to be a hundred, I want to live to be a hundred minus one day so I never have to live without you.
