Matematika Dasar   »   Integral   ›  Menghitung Luas suatu Daerah Menggunakan Integral

Menghitung Luas suatu Daerah Menggunakan Integral

Salah satu penerapan penting dari integral yaitu untuk mencari luas suatu bidang dengan bentuk yang tidak beraturan atau tidak tentu.

Salah satu penerapan penting dari integral yaitu untuk mencari luas suatu bidang dengan bentuk yang tidak beraturan. Anda mungkin masih ingat bahwa kita dapat mencari luas suatu daerah dengan bentuk tertentu seperti lingkaran, persegi, segitiga dan sebagainya dengan menggunakan rumus baku yang telah tersedia.

Sebagai contoh, kita dapat menghitung luas lingkaran menggunakan rumus baku yakni \(L = \pi \cdot r^2\), luas persegi dapat dihitung menggunakan rumus \( L = S \times S \), dan sebagainya.

Namun, bagaimana menentukan luas suatu bidang yang tidak beraturan atau yang belum mempunyai rumus baku untuk menghitung luasnya? Di sini kita akan membahas hal tersebut.

Perhatikanlah Gambar 1 berikut yang menunjukkan luasan area di bawah grafik \(y = f(x) = x^2\) yang dibatasi oleh \(x=0\) dan \(x=2\).

Gambar 1.

Kita tidak mempunyai rumus baku untuk menghitung luasan daerah seperti ini ketika kita menghitung luas suatu persegi, segitiga, dan sebagainya. Lalu, bagaimana mencari luasan daerah ini? Untuk menjawabnya, perhatikan dulu Gambar 2 berikut.

Gambar 2.

Luas area tersebut hampir mendekati luas dari total 7 persegi panjang. Jika jumlah persegi panjang tersebut terus diperbanyak hingga mendekati tak hingga maka luas dari seluruh persegi panjang akan sama dengan luas daerah R. Dengan kata lain, luas dari area R sama dengan limit dari luas seluruh persegi panjang yang banyaknya tak terhingga. Lihat Gambar 3 berikut.

Gambar 3.

Walaupun kelihatannya menarik mencari luas dengan menggunakan konsep limit, tapi kita tidak akan masuk terlalu detail terkait itu. Untuk tingkat sekolah menengah, Anda cukup mengingat bahwa luas suatu daerah yang dibatasi oleh \(x = a\) dan \(x = b\) dapat ditentukan dengan mengintegralkan fungsi tersebut pada selang \( a \leq x \leq b \). Kita nyatakan berikut ini.

Pengoperasian integral tentu sama dengan integral tak tentu, hanya saja nilai a dan b disubstitusikan dalam fungsi hasil integral yakni

Daerah di bawah sumbu x.

Luas daerah dinyatakan oleh bilangan yang tak negatif. Apabila grafik \(y=f(x)\) terletak di bawah sumbu-x maka \(∫_a^b f(x) \ dx\) adalah bilangan yang negatif, sehingga tak dapat menggambarkan suatu luas. Oleh karena itu, kita perlu mengalikan bilangan itu dengan negatif untuk luas daerah yang berada di bawah sumbu x

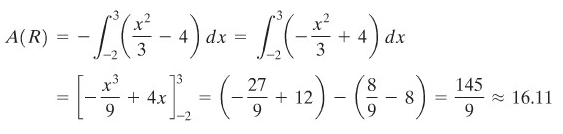
Luas di antara Dua Kurva

Selain untuk menghitung luas daerah yang berada di bawah kurva y = f(x) seperti yang telah kita pelajari di atas, kita juga dapat menghitung luas daerah yang berada di antara dua kurva menggunakan integral. Perhatikan Gambar 4 berikut.

Gambar 4.

Luas daerah yang diwarnai biru atau luas daerah di antara dua kurva dapat dicari dengan menggunakan konsep limit. Tapi, sekali lagi kita tidak akan membahas itu, Anda cukup mengingat bahwa luas daerah tersebut dapat ditentukan sebagai berikut.

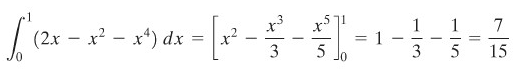
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.