Komposisi Fungsi, Contoh Soal dan Pembahasan

Matematika Dasar » Fungsi › Komposisi Fungsi, Contoh Soal dan Pembahasan

Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Komposisi Fungsi, Contoh Soal dan Pembahasan

Dari dua buah fungsi yakni \(f(x)\) dan \(g(x)\), kita dapat membentuk sebuah fungsi baru dengan menggunakan sistem operasi komposisi yang biasa dilambangkan dengan '∘'.

Komposisi dua fungsi merupakan penggabungan operasi dua fungsi secara berurutan yang akan menghasilkan sebuah fungsi baru. Misalkan diketahui fungsi \(f\) memetakan himpunan \(A\) ke himpunan \(B\) dan fungsi \(g\) memetakan himpunan \(B\) ke himpunan \(C\) sebagaimana diilustrasikan pada Gambar 1 berikut.

Gambar 1. Komposisi fungsi \(f\) dan \(g\)

Dari Gambar 1 di atas, untuk \( x \in A \) petanya adalah \( y = f(x) \) di \(B\), yang mana merupakan domain dari fungsi \(g\). Kemudian peta dari \( f(x) \in B \) yaitu \( g(y) = g(f(x)) \) di \(C\) yakni fungsi yang memetakan \(x\) dalam anggota \(A\) dengan tepat satu \( g(f(x)) \) anggota \(C\). Fungsi yang demikian disebut fungsi komposisi dari \(f\) dan \(g\), dan dinotasikan dengan \( (g \circ f) \) (dibaca: \(g\) bundaran \(f\)).

Secara singkat, jika \( f: A \to B \) dan \( g: B \to C \), maka kita peroleh komposisi dua fungsi berikut:

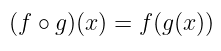
Perhatikan bahwa komposisi fungsi \( g \circ f \) adalah operasi berurutan yang mengerjakan \(f\) terlebih dulu, baru dilanjutkan oleh \(g\), sedangkan suatu operasi berurutan yang mengerjakan \(g\) terlebih dahulu, baru dilanjutkan oleh \(f\) merupakan komposisi fungsi \( f \circ g \).

Sekarang perhatikan Gambar 2 berikut.

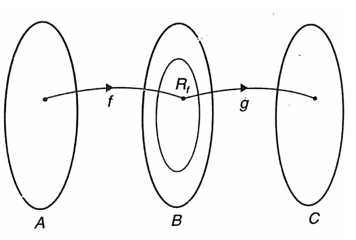
Gambar 2.

Dengan mengamati definisi komposisi fungsi dan diagram pada Gambar 2 di atas, maka dari dua buah fungsi \( f: A \to B \) dan \( g: B \to C \) dapat diperoleh komposisi fungsi \( g \circ f \) jika daerah hasil dari fungsi \(f\) atau \( R_f \) merupakan himpunan bagian dari B (domain \(g\) atau \(D_g\)).

Demikian juga, agar diperoleh komposisi fungsi \( f \circ g \), maka daerah hasil dari fungsi \(g\), \( (R_g) \), merupakan himpunan bagian dari domain \(f\).

Mari kita lihat beberapa contoh soal berikut.

Contoh 1:

Diketahui suatu fungsi \( f(x) = 3x - 1 \) dan \( g(x) = 2x^2 +3 \). Carilah nilai dari komposisi fungsi \( (g \circ f)(1) \)!

Pembahasan:

Diketahui \( f(x) = 3x - 1 \) dan \( g(x) = 2x^2 +3 \). Dengan demikian,

\begin{aligned} (g \circ f)(x) &= 2(3x-1)^2 + 3 \\[1em] &= 2 (9x^2 - 6x + 1) + 3 \\[1em] &= 18x^2 - 12x + 2 + 3 \\[1em] &= 18x^2 - 12 x + 5 \\[8pt] (g \circ f)(1) &= 18(1)^2-12(1)+5 \\[8pt] &= 11 \end{aligned}

Jadi, nilai \( (g \circ f)(1) \) adalah 11.

Contoh 2:

Misalkan diketahui fungsi \(g(x)= 3x + 2 \) dan \((g \circ f)(x) = 4x - 3 \). Tentukanlah fungsi \( f(x) \).

Pembahasan:

Diketahui \(g(x)= 3x + 2 \) dan \((g \circ f)(x) = 4x - 3 \). Dengan demikian,

\begin{aligned} (g \circ f)(x) &= 4x - 3 \\[1em] g(f(x)) &= 4x - 3 \\[1em] 3f(x) + 2 &= 4x - 3 \\[1em] 3 f(x) &= 4x - 3 - 2 \\[1em] f(x) &= \frac{4x-5}{3} \end{aligned}

Jadi, \( f(x) = \frac{4x-5}{3} \).

Contoh 3:

Jika diketahui \( \displaystyle{ f(x) = \frac{x}{x-1}, x \neq 1 } \) dan \( g(x) = f(x^2+1) \). Tentukan \( g(f(x)) \).

Pembahasan:

Kita modifikasi fungsi \( g(x) \) terlebih dahulu, yakni

\begin{aligned} g(x) &= f(x^2+1) \\[1em] &= \frac{(x^2+1)}{(x^2+1)-1} = \frac{x^2+1}{x^2} \\[1em] &= 1 + \frac{1}{x^2} \end{aligned}

Dengan demikian, kita peroleh

\begin{aligned} g(f(x)) &= 1 + \frac{1}{(f(x))^2} \\[1em] &= 1 + \frac{1}{\left( \frac{x}{x-1} \right)^2} \\[1em] &= 1 + \frac{x^2-2x+1}{x^2} \\[1em] &= 2 - \frac{2}{x} + \frac{1}{x^2} \end{aligned}

Contoh 4:

Jika \( f(x)=3x^2-2 \) dan \( g(x) = \frac{2x}{x-3} \) maka \( (f \circ g)(2) = \cdots \)

Pembahasan:

Berdasarkan informasi dalam soal, kita peroleh berikut:

\begin{aligned} (f \circ g)(x) &= f(g(x)) \\[1em] &= 3 \left( \frac{2x}{x-3} \right)^2-2 \\[1em] (f \circ g)(2) &= 3 \left( \frac{2 \cdot 2}{2-3} \right)^2 - 2 \\[8pt] &= 3 \cdot (-4)^2-2 \\[8pt] &= 46 \end{aligned}

Jawaban E.

Contoh 5:

Diketahui fungsi \( f: R \to R \) dan fungsi \(g: R \to R\) dirumuskan dengan \( f(x)=x-1 \) dan \( g(x)=x^2+2x-3 \). Fungsi komposisi \(g\) atas \(f\) dirumuskan dengan…

\( ( g \circ f )(x) = x^2-4 \)
\( ( g \circ f )(x) = x^2-5 \)
\( ( g \circ f )(x) = x^2-6 \)
\( ( g \circ f )(x) = x^2-4x-4 \)
\( ( g \circ f )(x) = x^2-4x-5 \)

Pembahasan:

Berdasarkan apa yang diketahui pada soal, kita peroleh berikut:

\begin{aligned} (g \circ f)(x) &= g(f(x)) \\[1em] &= (f(x))^2+2f(x)-3 \\[1em] &= (x-1)^2+2(x-1)-3 \\[1em] &= x^2-2x+1+2x-2-3 \\[8pt] &= x^2-4 \end{aligned}

Jawaban A.

Contoh 6:

Fungsi \(g: R \to R\) ditentukan oleh \( g(x) = x^2-3x+1 \) dan fungsi \(f:R \to R\) sehingga \( (f \circ g)(x) = 2x^2-6x-1 \). Maka \( f(x) = \cdots \)

\( 2x+3 \)
\( 2x+2 \)
\( 2x-1\)
\(2x-2\)
\(2x-3\)

Pembahasan:

Berdasarkan informasi pada soal, diperoleh:

\begin{aligned} (f \circ g)(x) &= 2x^2-6x-1 \\[1em] f(g(x)) &= 2x^2-6x-1 \\[1em] f(x^2-3x+1) &= 2(x^2-3x+1)-3 \end{aligned}

Jika kita misalkan \( x^2-3x+1 \) sebagai \(a\), maka kita peroleh \( f(a) = 2a-3 \). Kemudian ganti \(a\) dengan \(x\) sehingga diperoleh \( f(x) = 2x-3 \).

Jadi, fungsi \(f(x)\) adalah \( 2x-3 \).

Jawaban E.

Contoh 7:

Jika \( f(x) = \sqrt{x+1} \) dan \( ( f \circ g )(x) = 2\sqrt{x-1} \) maka fungsi \(g\) adalah \(g(x)= \cdots\)

\( 2x-1 \)
\( 2x-3 \)
\( 4x-5 \)
\( 4x-3 \)
\( 5x-4\)

Pembahasan:

Berdasarkan informasi dalam soal, kita peroleh:

\begin{aligned} (g \circ f)(x) &= 2\sqrt{x-1} \\[1em] g(f(x)) &= 2\sqrt{x-1} \\[1em] \sqrt{g(x)+1} &= 2\sqrt{x-1} \\[1em] \sqrt{g(x)+1} &= \sqrt{4(x-1)} \\[1em] g(x)+1 &= 4(x-1) \\[1em] g(x) &= 4x-4-1 \\[1em] &= 4x-5 \end{aligned}

Jawaban C.

Contoh 8:

Fungsi \( f:R \to R \) dan \( g: R \to R \) dinyatakan oleh \( f(x) = x+2 \) dan \( (g \circ f)(x) = 2x^2+4x+1 \). Maka \( g(2x) = \cdots \)

\( 2x^2+4x+1 \)
\( 2x^2-12x+1 \)
\( 8x^2-8x+1 \)
\( 8x^2+8x+1 \)
\( 4x^2-8x+1 \)

Pembahasan:

Dari soal diketahui \( (g \circ f)(x) = 2x^2+4x+1 \), sehingga diperoleh berikut:

\begin{aligned} (g \circ f)(x) &= 2x^2+4x+1 \\[1em] g(f(x)) &= 2x^2+4x+1 \\[1em] g(x+2) &= 2(x+2)^2-4x-7 \\[1em] g(x+2) &= 2(x+2)^2-4(x+2)+1 \\[1em] g(x) &= 2x^2-4x+1 \\[1em] g(2x) &= 2(2x)^2-4(2x)+1 \\[1em] &= 8x^2-8x+1 \end{aligned}

Jawaban C.

Contoh 9:

Diketahui \( f(x)=3x-6 \) dan \( g(x)=2x+a \). Bila \( (f \circ g)(x) = (g \circ f)(x) \) maka \(a = \cdots \)

5
3
-3
-4
-5

Pembahasan:

Berdasarkan informasi yang diketahui dari soal, kita peroleh nilai \(a\) sebagai berikut:

\begin{aligned} (f \circ g)(x) &= (g \circ f)(x) \\[1em] f(g(x)) &= g(f(x)) \\[1em] 3 g(x)-6 &= 2 f(x)+a \\[1em] 3(2x+a)-6 &= 2(3x-6)+a \\[1em] 6x+3a-6 &= 6x-12+a \\[8pt] 3a-a &= -12+6 \\[1em] 2a &= -6 \\[8pt] a &= -3 \end{aligned}

Jawaban C.

Contoh 10:

Diketahui \( f(x)=2-x \) dan \( g(x)=2x+a+1 \). Jika \( (f \circ g)(x) = ( g \circ f )(x) \), berapa nilai \(a\)?

-4
-2
0
2
4

Pembahasan:

Berdasarkan informasi pada soal, kita peroleh berikut:

\begin{aligned} (f \circ g)(x) &= (g \circ f)(x) \\[1em] f(g(x)) &= g(f(x)) \\[1em] f(2x+a+1) &= g(2-x) \\[1em] 2-(2x+a+1) &= 2(2-x)+a+1 \\[1em] 2-2x-a-1 &= 4-2x+a+1 \\[1em] 1-2x-a &= 5-2x+a \\[1em] 2a &= 1-2x-5+2x \\[1em] 2a &= -4 \\[1em] a &= -2 \end{aligned}

Jawaban B.

Cukup sekian ulasan singkat mengenai komposisi fungsi beserta contoh soal dan pembahasannya dalam artikel ini. Terima kasih telah membaca sampai selesai. Semoga bermanfaat.

Sumber:

Sunardi, Slamet Waluyo & Sutrisna. 2014. Konsep dan Penerapan Matematika SMA/MA Kelas XI. Jakarta: Penerbit PT Bumi Aksara.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.

www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

Matematika Dasar » Fungsi › Komposisi Fungsi, Contoh Soal dan Pembahasan