www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Persamaan Polinomial › Teorema Vieta: Rumus, contoh soal dan pembahasan
Teorema Vieta: Rumus, contoh soal dan pembahasan
Dalam matematika, Teorema Vieta adalah teorema yang berkaitan dengan rumus-rumus jumlah dan hasil kali akar-akar suatu persamaan suku banyak atau polinomial.
Dengan Teorema Vieta ini dapat diperoleh berbagai perhitungan akar-akar suatu persamaan polinomial walaupun kita tidak mengetahui nilai dari masing-masing akarnya. Ini dapat dilakukan dengan memanfaatkan informasi pada koefisien-koefisien dalam persaman suku banyak (polinomial) tersebut.
Adapun rumus jumlah dan hasil kali akar-akar suatu persamaan polinomial dapat dinyatakan sebagai berikut:
- Persamaan kuadrat:
- Persamaan kubik:
- Persamaan kuartik (Quartic):
- Persamaan kuintik (Quintic):

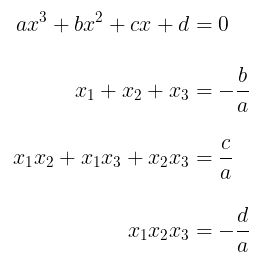


Contoh Soal dan Pembahasan
Beberapa contoh soal berikut akan memperdalam pemahaman terkait Teorema Vieta.
Contoh 1:
Persamaan kuadrat \( 2x^2 - 8x - 6 = 0 \) memiliki akar-akar \(α\) dan \(β\). Tentukanlah nilai dari
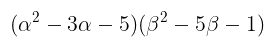
Pembahasan:
Dari Teorema Vieta untuk persamaan kuadrat, kita peroleh

Sekarang perhatikan bahwa
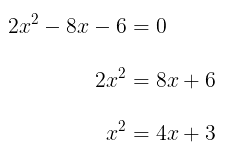
Nilai \(x\) dapat diganti dengan

Dengan demikian,

Contoh 2:
Persamaan \( x^3 + 6x^2 + 4x - 5 = 0 \) mempunyai akar-akar \( α, β \) dan \( γ \). Tentukan nilai dari \( α^3 + β^3 + γ^3 \).
Pembahasan:
Dari Teorema Vieta untuk persamaan kubik, kita peroleh

Terdapat dua cara untuk mencari nilai dari \( α^3 + β^3 + γ^3 \).
Cara pertama:
Perhatikan bahwa

Selanjutnya, persamaan semula dapat dituliskan kembali sebagai
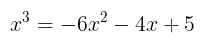
Jika kita mengganti nilai \(x\) dengan \( α, β \) dan \( γ \), maka kita peroleh

Jika ketiga persamaan dijumlahkan maka diperoleh
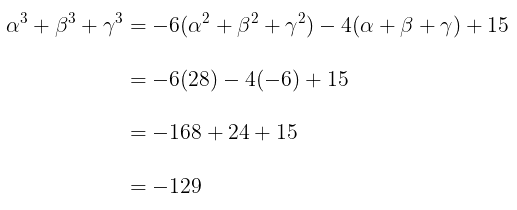
Cara kedua:
Dengan menggunakan hasil dari Teorema Vieta, kita peroleh

Contoh 3:
Akar-akar persamaan \( x^3 - 13x^2 + mx - 27 = 0 \) membentuk deret geometri. Nilai m = ...
Pembahasan:
Misalkan \( x_1 = a, \ x_2 = ar, \ x_3 = ar^2 \). Dari Teorema Vieta, kita peroleh

Jika nilai \( x_2 \) disubstitusikan ke persamaan semula, maka kita peroleh

Contoh 4:
Agar persamaan \( x^3 - x^2 - 8x + n = 0 \) memiliki sepasang akar kembar. Nilai n yang bulat adalah...
Pembahasan:
Karena terdapat sepasang akar kembar, kita dapat memisalkan sebagai berikut:

Dari Teorema Vieta untuk persamaan kubik, diperoleh

Selanjutnya, kita peroleh

Nilai \(α\) ini bisa menggantikan \(x\) pada persamaan semula, yakni

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Anda hidup hanya sekali, tetapi jika Anda melakukannya dengan benar, sekali itu cukup.
