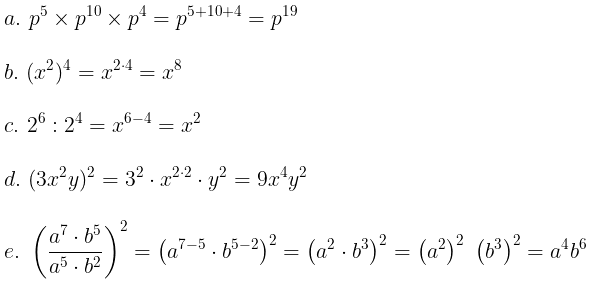Matematika Dasar   »   Bentuk Pangkat, Akar, dan Logaritma   ›  Bentuk Pangkat dan Sifat-sifatnya

Bentuk Pangkat

Bentuk Pangkat dan Sifat-sifatnya

Bentuk atau notasi pangkat (eksponen) digunakan untuk menuliskan bentuk perkalian dengan bilangan yang sama dan berulang-ulang dalam bentuk yang lebih sederhana. Dengan kata lain, notasi pangkat berguna untuk mempermudah dalam penulisan angka.

Sebagai contoh, jarak bumi ke matahari dapat dituliskan dalam bentuk pangkat \(1,5 \times 10^{11}\) m dan cepat rambat cahaya dapat dituliskan dalam bentuk \( 3 \times 10^8 \ ms^{-1} \). Tentu saja kegunaan pangkat tidak hanya itu, tapi ini adalah contoh yang bagus untuk pengantar materi kita.

Pangkat bilangan dalam matematika dapat berupa bilangan bulat positif atau bilangan asli, pangkat bulat negatif, pangkat nol, pangkat rasional dan pangkat riil. Kita akan membahas ini satu per satu.

Jika \(a\) adalah bilangan riil dan n bilangan bulat positif maka \(a^n\) (dibaca "a pangkat n") adalah hasil kali n buah faktor yang masing-masing faktornya adalah a. Jadi, secara umum pangkat bulat positif dapat dinyatakan sebagai

dengan: a = bilangan pokok (basis); n = pangkat atau eksponen; dan \(a^n\) = bilangan berpangkat.

Terdapat beberapa sifat-sifat bilangan berpangkat yang perlu anda ketahui, yakni

1. Sifat perkalian bilangan berpangkat.

Untuk \( a \in R \) dan m, n bilangan bulat positif, berlaku


2. Sifat pembagian bilangan berpangkat.

Untuk \( a \in R \) dan m, n bilangan bulat positif yang memenuhi m > n, berlaku


3. Sifat pangkat dari bilangan berpangkat.

Untuk \( a \in R \) dan m, n bilangan bulat positif, berlaku


4. Sifat pangkat dari perkalian bilangan.

Untuk \( a, b \in R \) dan n bilangan bulat positif, berlaku


5. Sifat pangkat dari pembagian bilangan.

Untuk \( a, b \in R, b \neq 0 \) dan n bilangan bulat positif, berlaku

Pangkat Bulat Nol

Untuk \(a\) adalah bilangan riil \( a \in R \) dan \(a\) bukan nol \((a\neq0)\) maka berlaku

Ini kita peroleh berdasarkan bahwa

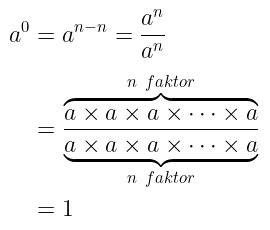
Perlu diperhatikan bahwa untuk a = 0, maka bentuk pangkat bulat nol menjadi tidak terdefinisi yakni

Pangkat Bulat Negatif

Tidak semua bilangan berpangkat bernilai positif, beberapa pangkat dapat berupa bilangan bulat negatif. Untuk \(a\) adalah bilangan riil (\( a \in R \)) dan \(a\) bukan nol \((a\neq0)\), maka berlaku

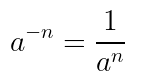
Ini kita peroleh berdasarkan kenyataan bahwa

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.