www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Persamaan Polinomial › Cara Menyusun Suatu Persamaan Kuadrat dan Contohnya
Cara Menyusun Suatu Persamaan Kuadrat dan Contohnya
Kita telah belajar berbagai cara mencari akar-akar persamaan kuadrat dan juga mencari jumlah dan hasil kali akar-akarnya berdasarkan koefisien-koefisien yang terdapat dalam persamaan kuadrat tersebut.
Sekarang kita akan mempelajari cara membentuk suatu persamaan kuadrat berdasarkan akar-akar persamaan kuadrat yang telah diketahui. Terdapat dua rumus untuk membentuk persamaan kuadrat. Rumus pertama dipakai jika diketahui nilai akar-akar persamaan kuadrat tersebut. Rumus kedua digunakan jika hanya diketahui informasi mengenai jumlah dan hasil kali akar-akarnya.
1. Cara Menyusun Persamaan Kuadrat Jika Diketahui Akar-akarnya
Jika akar-akar suatu persamaan kuadrat diketahui, maka suatu persamaan kuadrat dapat diperoleh dengan cara memasukkan atau mensubstitusi nilai dari akar-akarnya ke dalam persamaan berikut:

Agar lebih jelas, perhatikan beberapa contoh berikut:
2. Cara Menyusun Persamaan Kuadrat Jika Diketahui Diketahui Jumlah dan Hasil Kali Akar-akarnya
Dalam banyak kasus, sering kali kita hanya memiliki informasi mengenai jumlah dan hasil kali dari akar-akar persamaan kuadrat tersebut tanpa mengetahui nilai dari masing-masing akar-akarnya. Jika demikian halnya, maka kita dapat membentuk suatu persamaan kuadrat menggunakan rumus berikut:

Agar lebih jelas, perhatikan beberapa contoh berikut:
Contoh 1:
Suatu persamaan kuadrat \(2x^2-6x+3=0\) memiliki akar-akar \(p\) dan \(q\). Tentukan persamaan kuadrat baru dengan akar-akar \((p+q)\) dan \((2pq)\).
Pembahasan:
Berdasarkan persamaan \(2x^2-6x+3=0\) diketahui bahwa

Sehingga akar-akar dari persamaan kuadrat baru adalah
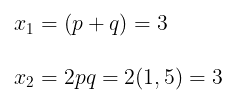
Dengan demikian, persamaan kuadrat baru tersebut adalah

Contoh 2:
Diketahui akar-akar persamaan kuadrat \( x^2 + 2x + 3 = 0 \) adalah \( \alpha \) dan \( \beta \). Persamaan kuadrat baru yang akar-akarnya \( (\alpha - 2) \) dan \( (\beta - 2) \) adalah
Pembahasan:
Berdasarkan persamaan kuadrat baru \( x^2 + 2x + 3 = 0 \), maka \( a = 1, \ b = 2 \) dan \(c = 3\). Maka jumlah dan hasil kali akar-akarnya adalah

Misalkan akar-akar dari persamaan kuadrat baru adalah \( x_1 \) dan \( x_2 \), yakni

Selanjutnya, carilah jumlah dan hasil kali dari akar-akar persamaan kuadrat baru yakni

Dengan demikian, kita peroleh
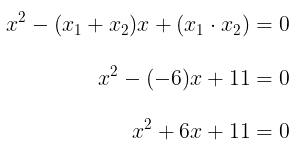
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
You cannot swim for new horizons until you have courage to lose sight of the shore.
