Matematika Dasar   »   Sistem Persamaan Linear   ›  Menyelesaikan Sistem Persamaan Linear Dua Variabel

Menyelesaikan Sistem Persamaan Linear Dua Variabel

Terdapat tiga metode untuk menyelesaikan permasalahan yang melibatkan sistem persamaan linear dua variabel yaitu metode grafik, metode substitusi dan metode eliminasi.

Sebuah garis dalam bidang \(xy\) secara aljabar dapat dinyatakan oleh persamaan yang berbentuk \(ax+by = c\). Persamaan semacam ini kita namakan persamaan linear dalam dua variabel yakni dalam variabel \(x\) dan variabel \(y\).

Terdapat tiga cara atau metode yang dapat digunakan untuk menyelesaikan permasalahan yang melibatkan sistem persamaan linear dua variabel, yakni

1. Metode grafik
2. Metode substitusi
3. Metode eliminasi

Kita akan menyelesaikan sistem persamaan liner dengan menggunakan metode substitusi dan metode eliminasi. Kita tidak akan membahas metode grafik di sini karena itu sangat jarang diterapkan mengingat kita harus menggambar grafik dan itu bukan pekerjaan yang efisien. Namun, tetap disarankan bagi anda untuk membacanya pada referensi yang lain.

Metode Substitusi

Beberapa langkah yang diperlukan untuk menerapkan metode ini yaitu:

1. Ubah salah satu persamaan menjadi bentuk \( y = ax + b \) atau \( x = cy +d \).
2. Substitusi persamaan \(x\) atau \(y\) yang diperoleh pada langkah pertama ke persamaan linear yang lainnya. Kemudian selesaikan persamaan untuk memperoleh nilai \(x\) atau \(y\).
3. Substitusi nilai \(x\) atau \(y\) yang diperoleh pada langkah kedua ke salah satu persamaan untuk memperoleh nilai dari variabel yang belum diketahui.
4. Tuliskan penyelesaiannya dalam \((x,y)\).

Beberapa contoh akan memperjelas apa yang dijelaskan di atas.

Contoh 1:

Cari nilai \(x\) dan \(y\) yang memenuhi sistem persamaan linear dua variabel berikut.

Pembahasan:

Kita akan menggunakan metode substitusi dengan mengikuti keempat langkah yang telah dijelaskan.

Langkah 1: Ubah salah satu persamaan menjadi bentuk \( y = ax + b \) atau \( x = cy +d \). Di sini kita akan mengubah persamaan \( 3x + y = 5 \) menjadi bentuk \( y = ax + b \). Kita peroleh sebagai berikut.

Langkah 2: Substitusi persamaan \(y\) yang diperoleh pada langkah 1 ke persamaan dua, lalu selesaikan persamaan untuk memperoleh nilai \(x\). Kita peroleh

Langkah 3: Substitusi nilai \(x\) yang diperoleh pada Langkah kedua ke salah satu persamaan. Kita akan substitusi nilai \(x = 1\) ke persamaan pertama, yakni

Langkah 4: Tuliskan penyelesaiannya ke dalam \((x,y)\). Jadi, himpunan penyelesaiannya adalah \((x,y) = (1,2)\).

Metode Eliminasi

Secara ringkas, dalam metode eliminasi kita menghilangkan atau mengeliminasi salah satu variabel untuk memperoleh nilai dari satu variabel lainnya. Beberapa langkah yang diperlukan untuk menerapkan metode eliminasi yakni

1. Menyamakan salah satu koefisien dari variabel \(x\) atau \(y\) dari kedua persamaan dengan cara mengalikan konstanta yang sesuai.
2. Eliminasi atau hilangkan variabel yang memiliki koefisien yang sama dengan cara menambahkan atau mengurangkan kedua persamaan, kemudian selesaikan persamaan untuk memperoleh nilai \(x\) atau \(y\).
3. Substitusi nilai \(x\) atau \(y\) yang diperoleh pada langkah 2 ke salah satu persamaan, kemudian selesaikan persamaan tersebut untuk memperoleh nilai variabel lain yang belum diketahui.
4. Tuliskan penyelesaiannya dalam \((x,y)\).

Contoh 2:

Cari nilai \(x\) dan \(y\) yang memenuhi sistem persamaan linear dua variabel berikut.

Pembahasan:

Perhatikan bahwa ini merupakan soal pada Contoh 1. Kita sengaja menggunakan contoh yang sama untuk menunjukkan bahwa penyelesaian sistem persamaan linear dengan beberapa metode yang disebutkan di atas akan menghasilkan nilai yang sama. Kita akan terapkan keempat langkah yang telah dijelaskan pada metode eliminasi, yakni

Langkah 1: Menyamakan salah satu koefisien dari variabel \(x\) atau \(y\) dari kedua persamaan. Di sini kita akan mengeliminasi variabel \(y\), sehingga kita harus menyamakan koefisien untuk variabel \(y\) pada kedua persamaan tersebut dengan cara mengalikan persamaan pertama dengan 1 dan mengalikan persamaan kedua dengan 3, yakni

Langkah 2: Eliminasi atau hilangkan variabel yang memiliki koefisien yang sama. Karena dari Langkah 1 koefisien variabel \(y\) telah sama, maka kita akan eliminasi variabel tersebut dan kemudian kita peroleh nilai untuk variabel \(x\), yakni

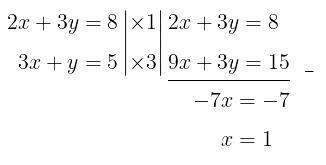
Langkah 3: Substitusi nilai \(x\) atau \(y\) yang diperoleh pada langkah 2 ke salah satu persamaan. Di sini kita akan substitusi nilai \(x = 1\) pada persamaan kedua untuk memperoleh nilai \(y\), yakni

Langkah 4: Tuliskan penyelesaian dalam \((x,y)\). Jadi, penyelesaian dari sistem persamaan linear yang diberikan adalah \((x,y) = (1,2)\).

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.