www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

Matematika Dasar   »   Turunan Fungsi   ›  Turunan Trigonometri, Contoh Soal dan Pembahasan
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Turunan Trigonometri, Contoh Soal dan Pembahasan

Konsep turunan juga berlaku untuk fungsi trigonometri seperti fungsi sinus, cosinus, dan tangen, serta kebalikan masing-masing fungsi tersebut yakni fungsi cosecan, secan, dan cotangen.

Pada artikel sebelumnya, kita telah membahas konsep turunan khususnya untuk fungsi aljabar beserta contoh soal dan pembahasannya. Sekarang kita akan lanjutkan materi tersebut untuk turunan yang melibatkan fungsi trigonometri seperti fungsi sinus (sin), cosinus (cos), dan tangen (tan), serta kebalikan dari masing-masing fungsi tersebut yakni fungsi cosecan (csc), secan (sec), dan cotangen (cot).

Ingat bahwa terdapat beberapa cara untuk menotasikan turunan yakni \(D_x, f'(x), y', \frac{d(f(x))}{dx}\) dan \( \frac{dy}{dx} \). Kita akan menggunakan beberapa notasi turunan tersebut secara bergantian pada artikel ini.

Proses pencarian turunan fungsi trigonometri akan banyak melibatkan rumus identitas trigonometri, sehingga sangat disarankan kamu untuk memahami materi tersebut terlebih dahulu.

Untuk mencari turunan fungsi sinus atau \(D(\sin⁡{x})\), kita bisa menggunakan definisi turunan dan identitas penambahan untuk \(\sin⁡{(x+h)}\). Kita peroleh sebagai berikut.

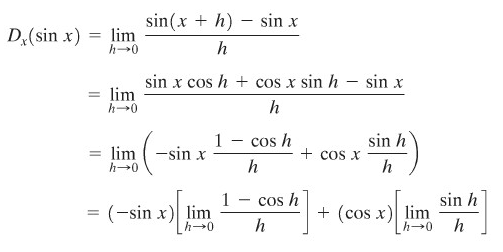
Gambar

Perhatikan bahwa dua limit pada dua ekspresi terakhir ini sesungguhnya merupakan limit yang telah kita pelajari pada pembahasan mengenai limit. Dan kita telah membuktikan bahwa

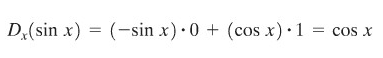
Gambar

Jadi,

Gambar

Dengan cara serupa, kita dapat mencari turunan fungsi cosinus yaitu

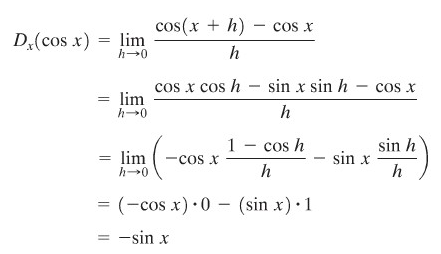
Gambar

Kita ringkaskan hasil-hasil ini dalam sebuah teorema penting.

TEOREMA:

Fungsi \(f(x) = \sin⁡{x}\) dan \(g(x) = \cos{⁡x}\) keduanya dapat didiferensialkan dan,

Gambar

Untuk mencari turunan fungsi tangen atau \(D(\tan⁡{x})\), kita bisa menggunakan definisi turunan dan identitas penambahan untuk \(\tan{(x+h)}\), yakni

Gambar

Sebenarnya ada cara mudah untuk mencari turunan dari fungsi tangen, yakni kita dapat gunakan kesamaan \( \tan x = \frac{\sin x}{\cos x} \) dan kemudian menerapkan rumus turunan untuk hasil bagi dua fungsi. Misalkan \( u = \sin x \) dan \( v = \cos x \), maka berdasarkan turunan untuk hasil bagi, kita peroleh

Gambar
Turunan Fungsi \( \csc x, \sec x \) dan \( \tan x \)

Untuk mencari turunan fungsi \( \csc x, \sec x \) dan \( \tan x \), kita dapat memanfaatkan kesamaan bahwa

Gambar

dan kemudian menerapkan rumus turunan untuk hasil bagi dua fungsi seperti yang telah kita contohkan untuk mencari turunan fungsi tangen. Dari hasil perhitungan diperoleh

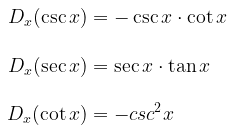
Gambar

Perhatikan beberapa contoh soal berikut:

Contoh 1:

Cari turunan dari \( f(x) = 3 \sin x - 2 \cos x \)

Pembahasan:

Gambar
Contoh 2:

Cari turunan dari \( y = 3 \sin 2x \).

Pembahasan:

Kita memerlukan turunan dari \(\sin⁡{2x}\); sayangnya, dari penjelasan di atas kita hanya tahu bagaimana mencari turunan dari \(\sin{x}\). Tetapi, karena \(\sin{2x} = 2 \sin{x} \cos{x}\), kita peroleh

Gambar
Contoh 3:

Diketahui \(f(x) = 2 \sin 2x\), maka turunan dari fungsi tersebut adalah \( f’(x) = \cdots \)

  1. \( 4 \cos x \)
  2. \( 4 \cos 2x \)
  3. \( 4 \sin x \)
  4. \( -4 \sin 2x \)
  5. \( 4 \sin 2x \)

Pembahasan:

Ingat bahwa turunan dari \( f(x) = a \sin bx \) adalah \(f’(x) = ab \cos bx\). Dengan demikian turunan dari \(f(x) = 2 \sin 2x\) adalah \( f’(x) = 4 \cos 2x \).

Jawaban B.

Contoh 4:

Diketahui \( f(x)=\sin^2 x \), maka turunan dari fungsi tersebut adalah \( f’(x) = \cdots \)

  1. \( 2 \sin x \cdot \cos x \)
  2. \( 2 \sin 2x \cdot \cos x \)
  3. \( 2 \sin x \cdot \cos 2x \)
  4. \( \sin^3 x \)
  5. \( 2 \sin x \)

Pembahasan:

Ingat bahwa untuk \( f(x) = u^n(x) \) di mana \( u(x) = g(x) \) maka turunan dari \(f(x)\) adalah \( f’(x) = nu^{n-1}(x) \cdot u’(x) \). Dalam kasus ini, turunan dari \( f(x) = \sin^2 x \) adalah \( f’(x) = 2 \sin x \cdot \cos x \).

Jawaban A.

Contoh 5:

Turunan pertama dari \( y = 3 \sin x -\cos x \) adalah \( y’ = \cdots \)

  1. \( 3 \cos x - \sin x \)
  2. \( 3 \cos x + \sin x \)
  3. \( \cos x + 3 \sin x \)
  4. \( -3 \cos x - \sin x \)
  5. \( -3 \cos x + \sin x \)

Pembahasan:

Turunan pertama dari \( y = 3 \sin x -\cos x \), yaitu:

\begin{aligned} y &= 3 \sin x -\cos x \\[8pt] y' &= 3 \cos x -(-\sin x) \\[8pt] &= 3 \cos x + \sin x \end{aligned}

Jawaban B.

Contoh 6:

Turunan pertama dari \( y = 2 \sin 3x-3 \cos 2x \) adalah \( y’ = \cdots \)

  1. \( 6 \cos 3x+6 \sin 2x \)
  2. \(6 \cos 3x-6 \sin 2x \)
  3. \( 6 \cos x + 6 \sin 2x \)
  4. \( 6 \cos 3x+6 \sin x \)
  5. \( 6 \cos x + 6 \sin x \)

Pembahasan:

Turunan pertama dari \(y\), yaitu:

\begin{aligned} y &= 2 \sin 3x-3 \cos 2x \\[8pt] y' &= 2 \cdot 3 \cos 3x - 3(-2\sin 2x) \\[8pt] &= 6 \cos 3x + 6\sin 2x \end{aligned}

Jawaban A.

Contoh 7:

Diketahui \( f(x) =x^4 \sin 2x \), maka turunan dari fungsi tersebut adalah \( f’(x) = \cdots \)

  1. \( x(x \cos 2x-2\sin 2x) \)
  2. \( x^2(\cos 2x+\sin 2x) \)
  3. \( x^3(\cos 2x+2\sin 2x) \)
  4. \( 2x^3(\cos 2x-2\sin 2x) \)
  5. \( 2x^3(x \cos 2x+2 \sin 2x) \)

Pembahasan:

Untuk menyelesaikan soal ini, kita perlu menggunakan sifat turunan perkalian. Misalkan \( u = x^4 \) dan \(v = \sin 2x\) sehingga diperoleh berikut:

\begin{aligned} f(x) &= x^4 \sin 2x \Leftrightarrow f(x) = u \cdot v \\[8pt] f'(x) &= u'v+uv' \\[8pt] &=4x^3 \cdot \sin 2x + x^4 \cdot 2 \cos 2x \\[8pt] &= 4x^3 \sin 2x + 2x^4 \cos 2x \\[8pt] &= 2x^3 (2 \sin 2x + x\cos 2x) \end{aligned}

Jawaban E.

Contoh 8:

Diketahui \( f(x) = \sin 2x \cos 3x \), maka turunan dari fungsi tersebut adalah \( f'\left(\frac{\pi}{4}\right) = \cdots \)

  1. \( -\frac{3}{2} \sqrt{2} \)
  2. \( -\frac{1}{2} \sqrt{2} \)
  3. \( 0 \)
  4. \( \sqrt{2} \)
  5. \( 3\sqrt{2} \)

Pembahasan:

Untuk menyelesaikan soal ini, kita bisa menggunakan rumus turunan perkalian, yakni misalkan \( u = \sin 2x \) dan \(v = \cos 3x\) sehingga diperoleh berikut ini:

\begin{aligned} f(x) &= \sin 2x \cos 3x \Leftrightarrow f(x) = u \cdot v \\[8pt] f'(x) &= u' \cdot v+u \cdot v' \\[8pt] &= 2\cos 2x \cdot \cos 3x + \sin 2x \cdot (-3 \sin 3x) \\[8pt] &= 2\cos 2x \cos 3x - 3 \sin 2x \sin 3x \\[8pt] f'\left(\frac{\pi}{4}\right) &= 2\cos 2\left(\frac{\pi}{4}\right) \cdot \cos 3\left(\frac{\pi}{4}\right) - 3 \sin 2\left(\frac{\pi}{4}\right) \cdot \sin 3\left(\frac{\pi}{4}\right) \\[8pt] &= 2 \cos 90^\circ \cdot \cos 135^\circ - 3 \sin 90^\circ \cdot \sin 135^\circ \\[8pt] &= 2 \cdot 0 \cdot \left( -\frac{1}{2}\sqrt{2}\right) - 3 \cdot 1 \cdot \left(\frac{1}{2}\sqrt{2}\right) \\[8pt] &= -\frac{3}{2}\sqrt{2} \end{aligned}

Jawaban A.

Contoh 9:

Diketahui \( f(x) = \sqrt{\cos 3x} \) maka turunan dari fungsi tersebut adalah \( f’(x) = \cdots \)

  1. \( -\frac{\sin 3x}{ 2 \sqrt{\cos 3x} } \)
  2. \( -\frac{3\sin 3x}{ 2 \sqrt{\cos 3x} } \)
  3. \( \frac{3\sin 3x}{ \sqrt{\cos 3x} } \)
  4. \( \frac{3\sqrt{\cos 3x}}{ 2\sin 3x } \)
  5. \( \frac{\sqrt{\cos 3x}}{ 2 \sin 3x } \)

Pembahasan:

Ingat bahwa untuk \( f(x) = \sqrt{u(x)} \) maka turunannya yaitu \( f’(x) = \frac{\cdot u’(x)}{2\sqrt{\cdot u’(x)}} \). Dengan demikian, turunan dari \(f(x) = \sqrt{\cos 3x}\), yaitu \( f'(x) = \frac{-3 \sin 3x}{2 \sqrt{\cos 3x}} \).

Jawaban B.

Contoh 10:

Diketahui \( f(x) = \frac{2+\cos x}{\sin x} \) maka turunan dari fungsi tersebut adalah \( f’(x) = \cdots \)

  1. \( \frac{1+2\cos x}{\sin^2 x} \)
  2. \( \frac{1-2\cos x}{\sin^2 x} \)
  3. \( \frac{-1+2 \cos x}{\sin^2 x} \)
  4. \( \frac{-1-2 \cos x}{\sin^2 x} \)
  5. \( \frac{1+2 \cos x}{ 2 \sin^2 x } \)

Pembahasan:

Untuk mengerjakan soal ini kita bisa gunakan sifat turunan pembagian, yakni misalkan \( u = 2 + \cos x \) dan \( v = \sin x \) sehingga diperoleh:

\begin{aligned} f(x) &= \frac{2+\cos x}{\sin x} \Leftrightarrow f(x) = \frac{u}{v} \\[8pt] f'(x) &= \frac{u' \cdot v-u \cdot v'}{v^2} \\[8pt] &= \frac{-\sin x \cdot \sin x - (2+\cos x) \cdot \cos x}{\sin^2 x} \\[8pt] &= \frac{-\sin^2 x-2\cos x-\cos^2 x}{\sin^2 x} \\[8pt] &= \frac{-(\sin^2x + \cos^2 x) - 2\cos x}{\sin^2 x} \\[8pt] &= \frac{-1-2\cos x}{\sin^2 x} \end{aligned}

Jawaban D.

Contoh 11:

Diketahui \( f(x) = \frac{1-\cos x}{\sin x} \), dengan \( \sin x \neq 0 \) maka \( f’(\frac{\pi}{4}) \) adalah…

  1. \( \sqrt{2}-1 \)
  2. \( \sqrt{2}+1 \)
  3. \( 1 \)
  4. \( 2-\sqrt{2} \)
  5. \( 2+\sqrt{2} \)

Pembahasan:

Untuk menyelesaikan soal ini kita bisa menggunakan rumus turunan pembagian, yakni misalkan \( u = 1-\cos x \) dan \(v = \sin x\) sehingga diperoleh:

\begin{aligned} f(x) &= \frac{1-\cos x}{\sin x} \Leftrightarrow f(x) = \frac{u}{v} \\[8pt] f'(x) &= \frac{u' \cdot v-u \cdot v'}{v^2} \\[8pt] &= \frac{-(-\sin x) \cdot \sin x - (1-\cos x) \cdot \cos x}{\sin^2 x} \\[8pt] &= \frac{\sin^2 x-\cos x+\cos^2 x}{\sin^2 x} \\[8pt] &= \frac{1-\cos x}{\sin^2 x} \\[8pt] f'\left( \frac{\pi}{4} \right) &= \frac{1-\cos \frac{\pi}{4}}{\sin^2 \frac{\pi}{4}} = \frac{1-\frac{1}{2}\sqrt{2}}{(\frac{1}{2}\sqrt{2})^2} \\[8pt] &= \frac{1-\frac{1}{2}\sqrt{2}}{\frac{1}{2}} = 2 - \sqrt{2} \end{aligned}

Jawaban D.

Contoh 12:

Diketahui \( f(x) = (1+x^2) \cos x \) maka \( f’(\pi) \) adalah…

  1. \( -\pi \)
  2. \( 0 \)
  3. \( -2\pi \)
  4. \( \pi+1 \)
  5. \( 2\pi-1 \)

Pembahasan:

Untuk menyelesaikan soal ini, bisa gunakan sifat turunan perkalian, yaitu misalkan \( u = (1+x^2) \) dan \(v=\cos x\) sehingga diperoleh:

\begin{aligned} f(x) &= (1+x^2) \cos x \Leftrightarrow f(x) = u \cdot v \\[8pt] f'(x) &= u' \cdot v+u \cdot v' \\[8pt] &= 2x \cdot \cos x + (1+x^2) \cdot (-\sin x) \\[8pt] &= 2x \cos x -(1+x^2) \sin x \\[8pt] f'(\pi) &= 2\pi \cdot \cos \pi-(1+\pi^2) \sin \pi \\[8pt] &= 2\pi \cdot (-1) -(1+\pi^2) \cdot 0 \\[8pt] &= -2\pi \end{aligned}

Jawaban C.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.

Artikel Terkait
img

Turunan komposisi fungsi dan aturan rantai

img

Fungsi trigonometri

img

Macam-macam rumus identitas trigonometri


The best and most beautiful things in this world cannot be seen or even heard, but must be felt with the heart.

Helen Keller