www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Matriks › Rumus Mencari Invers Matriks dan Contohnya
Rumus Mencari Invers Matriks dan Contohnya
Dua matriks A dan B dikatakan berkebalikan atau saling invers apabila AB = BA = I. Matriks A disebut invers matriks B dan matriks B disebut invers matriks A.
Salah satu topik bahasan penting dalam matriks yaitu invers matriks atau kebalikan dari matriks. Pada artikel ini akan dibahas bagaimana mencari invers dari suatu matriks terutama untuk matriks berukuran 2 x 2 dan 3 x 3.
Untuk mencari invers matriks yang berukuran lebih besar, Anda bisa membaca pada materi Aljabar Linear yang juga ada di website ini.
Invers Matriks Berordo 2 x 2
Misalkan diketahui matriks

dengan determinan A adalah
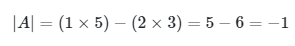
dan misalkan lagi matriks C adalah matriks yang diperoleh dengan menukarkan tempat elemen-elemen diagonal utama dan mengganti tanda dari elemen-elemen diagonal kedua dari matriks A yakni

Kemudian, jika terdapat matriks B yang didefinisikan sebagai

Maka

Sekarang perhatikan perkalian dua matriks A dan B berikut:

Tampak bahwa hasil kali matriks A dan B, yaitu AB = BA = I, merupakan matriks identitas. Dua matriks yang demikian dikatakan berkebalikan atau saling invers. Matriks A disebut invers matriks B dan matriks B disebut invers matriks A. Dikatakan pula bahwa matriks A memiliki invers, yaitu matriks B. Dengan demikian, matriks A akan memiliki invers, jika ada matriks B sedemikian sehingga AB = BA = I.
Berikut ini adalah syarat suatu matriks A memiliki invers.
- Jika \(|A| = 0\) maka matriks A tidak memiliki invers. Matriks A disebut matriks singular.
- Jika \(|A| ≠ 0\) maka matriks A memiliki invers. Matriks A yang demikian disebut matriks non-singular.
Dari uraian di atas, dapat disimpulkan bahwa untuk matriks A yang berorodo 2 x 2, yakni
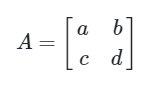
dapat ditentukan inversnya yaitu

Perhatikan bahwa kita menggunakan notasi \( A^{-1} \) untuk menyatakan invers matriks.
Perhatikan contoh soal berikut:
Contoh 1:
Diketahui 3 buah matriks yaitu:

Manakah pasangan matriks yang saling invers?
Pembahasan:
Ingat bahwa dua matriks P dan Q akan saling invers jika memenuhi PQ = I dan QP = I, atau PQ=QP=I, di mana I adalah mariks identitas. Jadi, untuk menemukan pasangan matriks yang saling invers, kita perlu mencari kombinasi perkalian antara tiga matriks tersebut, yakni perkalian antara AB, AC atau CA, dan BC.

Karena hasil kali AB bukan matriks identitas, maka A dan B tidak saling invers. Dalam hal ini, kita tidak perlu lagi mencari hasil kali BA, karena salah satu syarat sudah tidak terpenuhi.
Selanjutnya,
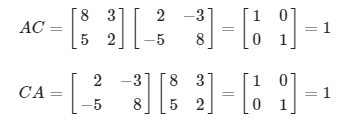
Karena AC = BC = I, maka matriks A dan matriks C adalah saling invers.
Berikutnya,

Karena hasil kali BC bukan matriks identitas, maka B dan C tidak saling invers.
Dari hasil di atas, dapat kita simpulkan bahwa pasangan matriks yang saling invers adalah matriks A dan C.
Contoh 2:
Jika matriks
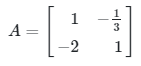
adalah invers dari matriks

maka tentukanlah nilai dari \(x\) dan \(y\).
Pembahasan:
Jika matriks A adalah invers dari matriks B maka \(AB = I\) atau \(B = A^{-1}\)

Dengan demikian, kita peroleh persamaan berikut

Karena entri-entri yang bersesuaian adalah sama, maka kita peroleh

Jadi, nilai \(x\) dan \(y\) berturut-turut adalah -1 dan 5.
Invers Matriks Berordo 3 x 3
Untuk menentukan invers matriks berordo 3 x 3 kita perlu mengenal apa yang dimaksud dengan minor entri, kofaktor dan adjoint. Misalkan terdapat matriks
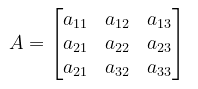
Minor entri \( a_{ij} \) yang dinotasikan dengan \( M_{ij} \) didefinisikan sebagai determinan submatriks setelah baris ke-i dan kolom ke-j dicoret dari A. Bilangan \( (-1)^{(i+j)} M_{ij} \) yang dinotasikan \( C_{ij} \) disebut kofaktor entri \( a_{ij} \).
Contoh 3:
Misalkan

maka minor entri \(a_{11}\) adalah
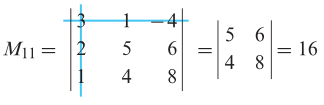
Kofaktor \(a_{11}\) adalah
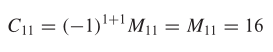
Demikian juga, minor entri \(a_{32}\) adalah
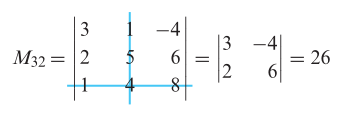
Kofaktor \(a_{32}\) adalah
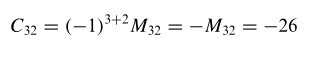
Perhatikan bahwa kofaktor dan minor elemen \(a_{ij}\) hanya berbeda dalam tandanya, yakni, \(C_{ij} = ± M_{ij}\). Cara cepat untuk menentukan apakah penggunaan tanda + atau tanda – didasarkan pada kenyataan bahwa tanda yang menghubungkan \(C_{ij}\) dan \(M_{ij}\) berada dalam baris ke \(i\) dan kolom ke \(j\) dari susunan berikut

Misalnya, \(C_{ij}= M_{ij}, C_{21} = -M_{21}, C_{12} = -M_{12}, C_{22} = M_{22}\), dan seterusnya.
Kita telah mengenal apa itu minor entri dan kofaktor, sekarang ada satu istilah lagi yang perlu diketahui sebelum sampai pada definisi invers matriks 3 x 3 yaitu apa yang dikenal dengan adjoint.
Definisi: Adjoint
Jika \(A\) adalah sebarang matriks \(n × n\) dan \(C_{ij}\) adalah kofaktor \(a_{ij}\), maka matriks

dinamakan matriks kofaktor \(A\). Transpos matriks ini dinamakan adjoin \(A\) dan dinyatakan \(\text{adj}(A)\).
Jadi, definisi invers matriks berukuran 3 x 3 diberikan sebagai berikut.
Definisi: Invers Matriks 3 x 3
Jika \(A\) adalah matriks yang dapat dibalik, maka
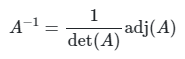
Contoh 4: Mencari Invers Matriks
Misalkan diketahui matriks A sebagai berikut.
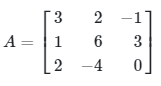
Tentukanlah invers dari matriks A.
Pembahasan:
Untuk mencari invers matriks A kita perlu menentukan minor entri, kofaktor dan adjoin dari matriks A terlebih dahulu. Kofaktor matriks \(A\) yaitu

Sehingga matriks kofaktor nya adalah
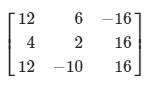
Untuk menentukan adjoin \(A\), kita hanya perlu melakukan transpos pada matriks kofaktor. Kita peroleh

Untuk Contoh ini, kita peroleh \(\det(A) = 64\). Jadi,

Persamaan Matriks
Hasil kali suatu matriks A yang nonsingular dengan matriks inversnya merupakan matriks identitas, yaitu \(AA^{-1}=A^{-1} A=I\). Namun, hasil kali antara suatu matriks A dengan matriks identitas merupakan matriks A, yaitu \(AI = IA = A\). Kedua konsep tersebut dapat digunakan untuk menyelesaikan persamaan matriks.
Sebagai contoh, misalkan kita ingin menentukan suatu matriks \(X\) sedemikian sehingga memenuhi persamaan matriks \(AX = B\) atau \(XA = B\). Matriks \(X\) ditentukan dengan langkah-langkah sebagai berikut.

Dengan demikian, didapatkan sifat-sifat berikut.
- Jika \(AX = B\), maka \(X = A^{-1}B\), dengan \(|A|≠0\)
- Jika \(XA = B\) maka \(X=BA^{-1}\) dengan \(|A|≠0\)
Persamaan-persamaan matriks yang lain dapat diselesaikan dengan langkah-langkah yang sama. Untuk lebih jelasnya, perhatikan contoh soal berikut.
Contoh 5:
Tentukanlah matriks \(X\) berordo 2 x 2 yang memenuhi:
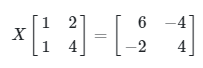
Pembahasan:
Untuk menjawab soal ini misalkanlah

maka bentuk persamaan dari soal berlaku sifat:

Dengan demikian, kita peroleh

Jadi, \( X = \left[ {\begin{array}{rr} 14 & -8 \\ -6 & 4 \\ \end{array} } \right] \)
Contoh 6:
Jika \( B = \left[ {\begin{array}{rr} 1 & 2 \\ 3 & 5 \\ \end{array} } \right] \) dan \( AB^{-1} = \left[ {\begin{array}{rr} 2 & 1 \\ 4 & 3 \\ \end{array} } \right] \), maka tentukanlah matriks A!
Pembahasan:

Sumber:
Sunardi, Slamet Waluyo & Sutrisna. 2014. Konsep dan Penerapan Matematika SMA/MA Kelas XI. Jakarta: Penerbit PT Bumi Aksara.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Meeting you was fate, becoming your friend was a choice, but falling in love with you was beyond my control.
