Jumlah dan Hasil Kali Akar-akar Persamaan Kuadrat

Matematika Dasar » Persamaan Polinomial › Jumlah dan Hasil Kali Akar-akar Persamaan Kuadrat

Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Jumlah dan Hasil Kali Akar-akar Persamaan Kuadrat

Kita bisa menghitung jumlah dan hasil kali akar-akar suatu persamaan kuadrat berdasarkan informasi pada koefisien-koefisien dalam persamaan kuadrat tersebut.

Kita bisa menghitung jumlah dan hasil kali akar-akar suatu persamaan kuadrat tanpa harus mencari nilai dari masing-masing akar-akarnya. Hal ini dapat dilakukan berdasarkan informasi yang terdapat pada koefisien-koefisien dalam persamaan kuadrat tersebut.

Anda mungkin masih ingat bahwa dari rumus abc, akar-akar persamaan kuadrat dapat diperoleh dengan

Dengan menjumlahkan akar-akar persamaan kuadrat tersebut akan memberikan kita rumus baru yakni

Dengan mengurangkan akar-akar persamaan kuadrat, diperoleh:

\begin{aligned} x_1-x_2 &= \frac{-b+\sqrt{b^2-4ac}}{2a}-\frac{-b-\sqrt{b^2-4ac}}{2a} \\[8pt] &= \frac{-b+\sqrt{b^2-4ac}+b+\sqrt{b^2-4ac}}{2a} \\[8pt] &= \frac{2\sqrt{b^2-4ac}}{2a} = \frac{\sqrt{b^2-4ac}}{a} \\[8pt] x_2-x_1 &= \frac{-b-\sqrt{b^2-4ac}}{2a}-\frac{-b+\sqrt{b^2-4ac}}{2a} \\[8pt] &= \frac{-b-\sqrt{b^2-4ac}+b-\sqrt{b^2-4ac}}{2a} \\[8pt] &= \frac{-2\sqrt{b^2-4ac}}{2a} = \frac{-\sqrt{b^2-4ac}}{a} \\[8pt] \text{Jadi selisih} \ &x_1 \ \text{dan} \ x_2 \ \ \text{adalah} \ \pm \frac{\sqrt{b^2-4ac}}{a} \end{aligned}

Sedangkan, perkalian akar-akar persamaan kuadrat tersebut akan menghasilkan

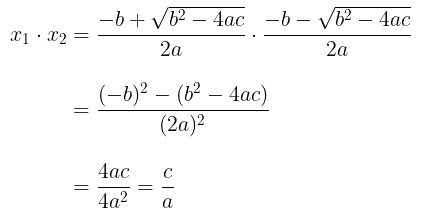
Dengan demikian, rumus jumlah, selisih, dan hasil kali akar-akar persamaan kuadrat adalah sebagai berikut:

\begin{aligned} x_1+x_2 &= -\frac{b}{a} \\[8pt] x_1-x_2 &= \pm \frac{\sqrt{b^2-4ac}}{a} \\[8pt] x_1 \cdot x_2 &= \frac{c}{a} \end{aligned}

Adapun perluasan dari rumus di atas yaitu:

\begin{aligned} x_1^2+x_2^2 &= (x_1+x_2)^2-2x_1 \cdot x_2 \\[8pt] x_1^3+x_2^3 &= (x_1+x_2)^3-3x_1 \cdot x_2 (x_1+x_2) \\[8pt] x_1^2-x_2^2 &= (x_1+x_2)(x_1-x_2) \\[8pt] x_1^3-x_2^3 &= (x_1-x_2)^3+3x_1 \cdot x_2 (x_1-x_2) \\[8pt] x_1^4+x_2^4 &= \left[ (x_1+x_2)^2-2x_1x_2 \right]^2-2(x_1x_2)^2 \\[8pt] x_1^4-x_2^4 &= \left[ (x_1+x_2)^2-2x_1x_2 \right]^2 \left[ (x_1-x_2)(x_1+x_2) \right] \end{aligned}

Contoh soal dan pembahasan:

Agar lebih jelas, perhatikan beberapa contoh soal berikut:

Contoh 1:

Suatu persamaan kuadrat \(x^2-2x-4=0\) memiliki akar-akar \(p\) dan \(q\). Tentukan nilai dari \((p^2-q^2)^2\).

Pembahasan:

Berdasarkan persamaan \(x^2-2x-4=0\) diketahui bahwa

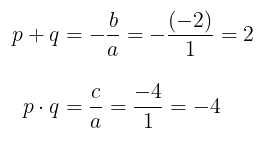
Dengan demikian, kita peroleh

Contoh 2:

Akar-akar dari \( 2x^2-6x-p = 0 \) adalah \(x_1\) dan \(x_2\). Jika \(x_1-x_2=5\) maka nilai \(p\) adalah…

Pembahasan:

Dari persamaan kuadrat \( 2x^2-6x-p=0 \) diperoleh koefisien \(a = 2, b = -6\) dan \(c = -p\). Ingat bahwa rumus selisih akar persamaan kuadrat adalah \( x_1-x_2 = \frac{\sqrt{b^2-4ac}}{a} \) sehingga diperoleh:

\begin{aligned} x_1-x_2 &= \frac{\sqrt{b^2-4ac}}{a} \\[8pt] 5 &= \frac{\sqrt{(-6)^2-4(2)(-p)}}{2} \\[8pt] 10 &= \sqrt{36+8p} \\[8pt] 100 &= 36+8p \\[8pt] p &= \frac{100-36}{8} = \frac{64}{8} \\[8pt] &= 8 \end{aligned}

Contoh 3:

Persamaan kuadrat \( x^2-ax+a+1 = 0 \) mempunyai akar-akar \(x_1\) dan \(x_2\). Jika \(x_1-x_2=1\) maka nilai \(a= \cdots\)

Pembahasan:

Dari persamaan kuadrat \( x^2-ax+a+1 = 0 \) diperoleh koefisien \(a = 1, b=-a\) dan \(c=a+1\). Ingat bahwa rumus selisih akar persamaan kuadrat adalah \( x_1-x_2 = \frac{\sqrt{b^2-4ac}}{a} \) sehingga diperoleh:

\begin{aligned} x_1-x_2 &= \frac{\sqrt{b^2-4ac}}{a} \\[8pt] 1 &= \frac{(-a)^2-4(1)(a+1)}{1} \\[8pt] 1 &= a^2-4a-4 \\[8pt] 0 &= a^2-4a-5 \\[8pt] 0 &= (a-5)(a+1) \\[8pt] a &= 5 \ \text{atau} \ a = -1 \end{aligned}

Contoh 4:

Akar-akar persamaan \( 3x^2+2x-5=0 \) adalah \( x_1 \) dan \(x_2\). Nilai dari \( \frac{1}{x_1}+\frac{1}{x_2} = \cdots \)

Pembahasan:

Dari persamaan \( 3x^2+2x-5=0 \) diperoleh koefisien \(a=3, b=2\) dan \(c=-5\) sehingga berdasarkan rumus jumlah dan hasil kali akar-akar persamaan kuadrat, diperoleh:

\begin{aligned} x_1+x_2 &= -\frac{b}{a} = -\frac{2}{3} \\[8pt] x_1 \cdot x_2 &= \frac{c}{a} = \frac{-5}{3} \end{aligned}

Dengan demikian, diperoleh:

\begin{aligned} \frac{1}{x_1}+\frac{1}{x_2} &= \frac{x_2+x_1}{x_1 \cdot x_2} = \frac{-2/3}{-5/3} \\[8pt] &= \frac{2}{5} \end{aligned}

Contoh 5:

Jika kedua akar persamaan \( \frac{x^2-bx}{ax-c} = \frac{m-1}{m+1} \) saling berlawanan tanda, tetapi mempunyai nilai mutlak yang sama maka nilai \(m\) sama dengan…

Pembahasan:

Lakukan manipulasi pada persamaan \( \frac{x^2-bx}{ax-c} = \frac{m-1}{m+1} \) sehingga diperoleh:

\begin{aligned} &\frac{x^2-bx}{ax-c} = \frac{m-1}{m+1} \\[8pt] &(m+1)(x^2-bx) = (m-1)(ax-c) \\[8pt] &(m+1)x^2-(m+1)bx = (m-1)ax-(m-1)c \\[8pt] &(m+1)x^2-(mb+b)x-(ma-a)x+(m-1)c = 0 \\[8pt] &(m+1)x^2-(mb+b+ma-a)x+(m-1)c = 0 \end{aligned}

Misalkan akar-akarnya \(x_1\) dan \(x_2\). Karena diketahui akar-akarnya berlainan tanda maka \(x_1 = -x_2\) atau \(x_1+x_2 = 0\) sehingga diperoleh:

\begin{aligned} & x_1+x_2 = 0 \\[8pt] & \frac{mb+b+ma-a}{m+1} = 0 \\[8pt] & mb+b+ma-a = 0 \\[8pt] & (b+a)m = a-b \\[8pt] & m = \frac{a-b}{b+a} = \frac{a-b}{a+b} \end{aligned}

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.

www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

Matematika Dasar » Persamaan Polinomial › Jumlah dan Hasil Kali Akar-akar Persamaan Kuadrat