www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Persamaan Polinomial › Mencari Akar-akar Persamaan Kuadrat dengan Melengkapkan Kuadrat Sempurna
Mencari Akar-akar Persamaan Kuadrat dengan Melengkapkan Kuadrat Sempurna
Pada artikel sebelumnya, kita telah membahas cara mencari akar-akar persamaan kuadrat dengan pemfaktoran. Beberapa di antara kalian pasti telah menyadari bahwa kita tidak selalu bisa mencari akar-akar persamaan kuadrat dengan cara demikian.
Dengan kata lain, terkadang kita akan menjumpai bentuk persamaan kuadrat yang tidak memungkinkan untuk mencari akar-akarnya dengan pemfaktoran atau bentuk persamaan kuadrat tersebut sangat sulit dipecah ke dalam perkalian faktor-faktornya.
Sebagai contoh, sangat sulit mencari akar-akar persamaan kuadrat \(x^2-10x+1=0\) dengan cara pemfaktoran karena faktor-faktor dari persamaan tersebut merupakan bilangan irasional. Kita dapat mengatasi masalah mencari akar-akar persamaan kuadrat ini dengan alternatif lain yakni dengan cara melengkapkan kuadrat sempurna (cara lainnya bisa gunakan rumus abc).
Prinsip dari metode ini adalah memanipulasi secara aljabar persamaan kuadrat sehingga menjadi bentuk kuadrat sempurna. Penyelesaian persamaan kuadrat dengan melengkapkan kuadrat menggunakan rumus berikut.

Ubahlah sehingga menjadi bentuk

Untuk memanipulasi persamaan kuadrat sehingga menjadi bentuk di atas, kita dapat menggunakan rumus berikut:

Setelah diperoleh bentuk \( (x+p)^2 = q \), tentukanlah akar-akarnya dengan cara sebagai berikut:

Berikut adalah langkah-langkah untuk mencari akar-akar persaman kuadrat \(ax^2+bx+c=0\) dengan cara melengkapkan kuadrat sempurna:
- Pindahkan konstanta \(c\) dari ruas kiri ke ruas kanan persamaan.
- Bagi kedua ruas persamaan dengan \(a\) (koefisien suku \(x^2\)).
- Hitunglah \(\left(\frac{1}{2} \cdot (-\frac{b}{a})\right)^2\) dan jumlahkan kedua ruas dengan hasilnya.
- Faktorkan ruas kiri sebagai kuadrat binomial; kemudian sederhanakan ruas kanan.
- Selesaikan dengan menggunakan sifat akar kuadrat dari suatu persamaan.
Contoh Soal dan Pembahasan
Perhatikan beberapa contoh berikut ini.
Contoh 1:
Dengan menggunakan cara melengkapkan kuadrat sempurna, carilah akar-akar persamaan kuadrat \(x^2-10x+1=0\).
Pembahasan:
Pertama, kita memindahkan nilai \(c = 1\) ke ruas kanan persamaan, kemudian membagi kedua ruas persamaan dengan \(a = 1\). Karena pembagian dengan 1 tidak mengubah apapun, kita peroleh hasil berikut.

Selanjutnya, hitunglah \(\left(1/2 ⋅ (-\frac{b}{a})\right)^2\), yaitu

Jumlahkan kedua ruas dengan hasil yang diperoleh di atas, sehingga
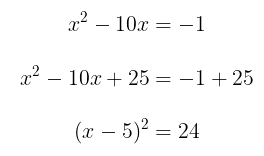
Dengan demikian, kita peroleh

Jadi, akar-akar dari persamaan kuadrat tersebut yaitu \( x_1 = 5 + 2\sqrt{6} \) dan \( x_2 = 5 - 2\sqrt{6} \).
Contoh 2:
Tentukan akar-akar persamaan kuadrat \( 2x^2 - 5 x + 3 = 0 \) dengan cara melengkapkan kuadrat sempurna.
Pembahasan:
Pertama, kita memindahkan nilai \(c = 3\) ke ruas kanan persamaan, kemudian membagi kedua ruas persamaan dengan \(a = 2\). Kita peroleh hasil berikut.

Selanjutnya, hitunglah \(\left(1/2 ⋅ (-\frac{b}{a})\right)^2\), yaitu

Jumlahkan kedua ruas dengan hasil yang diperoleh di atas, sehingga

Dengan demikian, kita peroleh

Jadi, akar-akar dari persamaan kuadrat tersebut yaitu \( x_1 = 6/4 \) dan \( x_2 = 1 \).
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Jika kamu kehilangan seseorang, tapi menemukan dirimu yang sebenarnya, kamu menang.
