www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Bentuk Pangkat, Akar, dan Logaritma › Logaritma dan Sifat-sifatnya
Logaritma dan Sifat-sifatnya
Pada artikelnya sebelumnya kita telah membahas tentang bentuk pangkat. Misalnya, \(2^4 = 16\) di mana 2 disebut basis, 4 disebut pangkat (eksponen), dan 16 sebagai hasil pemangkatan 2 oleh 4.
Jika pertanyaannya dibalik yakni 2 pangkat berapa menghasilkan nilai 16? Anda akan menjawab 4. Operasi kebalikan dari semula menentukan nilai pemangkatan menjadi menentukan pangkatnya disebut operasi logaritma, yang dapat dituliskan sebagai

Secara umum, jika \( x = a^n \) maka \( {}^a \log x = n \) dan sebaliknya jika \( {}^a \log x = n \) maka \( x = a^n \). Jadi, hubungan antara bilangan berpangkat dan logaritma dapat dinyatakan dengan

di mana: \(a\) = bilangan pokok atau basis, \( a > 0, a \neq 1 \); \(x\) = numerus (yang dicari nilai logaritmanya), \(x > 0\); dan \(n\) = hasil logaritma. (\( {}^a \log x \) dibaca "logaritma \(x\) dengan basis \(a\)")
Jadi, bentuk logaritma dapat dinyatakan dalam bentuk pangkat dan sebaliknya, bentuk pangkat dapat dinyatakan dalam bentuk logaritma.
Contoh 1:
Nyatakan logaritma berikut dalam bentuk pangkat.

Pembahasan:
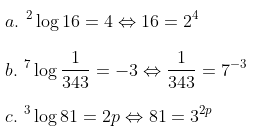
Contoh 2:
Nyatakan bentuk pangkat berikut ke dalam bentuk logaritma.
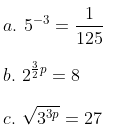
Pembahasan:

Sifat-sifat Logaritma
Berikut ini diberikan beberapa sifat logaritma yang penting dan sering dipakai untuk menyelesaikan berbagai soal terkait logaritma.
#1. Sifat 1
Untuk \(a > 0, a \neq 1\), berlaku:
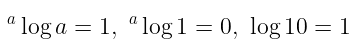
#2. Sifat 2
Untuk \(a > 0, a \neq 1, x > 0\) dan \( y > 0 \) serta a, x dan \(y \in R\) berlaku:

#3. Sifat 3
Untuk \(a > 0, a \neq 1, x > 0\) dan \( y > 0 \) serta a, x dan \(y \in R\) berlaku:

#4. Sifat 4
Untuk \(a > 0, a \neq 1, a, n, \) dan \(x \in R\) berlaku:
\[ {}^a \log x^n = n \cdot {}^a \log x \]
#5. Sifat 5
Untuk \(a, m > 0\), serta \(a, m, n, x \in R\), berlaku:
\[ {}^{a^m} \log x^n = \frac{n}{m} \cdot {}^a \log x \]
Contoh 3:
Sederhanakan bentuk logaritma berikut.

Pembahasan:



Contoh 4:
Tentukan nilai \(x\) dari bentuk logaritma berikut:
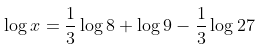
Pembahasan:
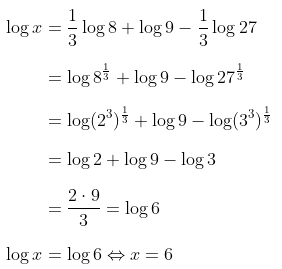
#6. Sifat 6
Untuk \(a, p > 0\), dan \(a, p \neq 1\), serta \(a, p\), dan \(x \in R\), berlak:

#7. Sifat 7
Untuk \( a > 0, x > 0, y > 0, a, x, \) dan \( y \in R \), berlaku:
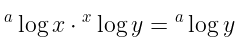
#8. Sifat 8
Untuk \( a > 0 \), serta \(a\) dan \( x \in R \), berlaku:

#9. Sifat 9
Untuk \(a > 0\), serta \(a\) dan \(x \in R\), berlaku:
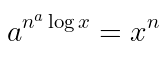
Contoh 5:
Jika \( {}^2 \log 3 = a \) dan \( {}^3 \log 5 = b \), nyatakan \( {}^{12} \log 30 \) dalam \(a\) dan \(b\).
Pembahasan:

Contoh 6:
Sederhanakanlah bentuk logaritma berikut.

Pembahasan:


Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Bila kamu tak tahan lelahnya belajar, maka kamu akan menanggung perihnya kebodohan.
