Matematika Dasar   »   Pertidaksamaan   ›  Pertidaksamaan Kuadrat: Rumus, contoh soal dan pembahasan

Pertidaksamaan Kuadrat: Rumus, contoh soal dan pembahasan

Menyelesaikan pertidaksamaan kuadrat atau menentukan himpunan penyelesaian pertidaksamaan kuadrat diawali dengan mencari akar-akar pertidaksamaan kuadrat tersebut.

Menyelesaikan pertidaksamaan kuadrat atau menentukan himpunan penyelesaian pertidaksamaan kuadrat diawali dengan mencari akar-akar pertidaksamaan kuadrat tersebut. Cara menentukan akar-akar pertidaksamaan kuadrat tidak jauh berbeda dengan mencari akar-akar persamaan kuadrat. Hanya saja, dalam menemukan akar-akar pertidaksamaan kuadrat diperlukan beberapa langkah tambahan.

Jika Anda mengikuti materi yang ada di website ini, anda harusnya telah belajar bahwa terdapat tiga cara mencari akar-akar persamaan kuadrat yakni dengan pemfaktoran, melengkapkan kuadrat sempurna, dan rumus abc. Kita tidak akan mengulangnya lagi di sini. Jadi, sangat disarankan bagi Anda untuk membaca materi tersebut terlebih dahulu.

Berikut adalah beberapa contoh pertidaksamaan kuadrat:

1. \(x^2-x-12 \geq 0\)
2. \(x^2-8x+15 \leq 0\)
3. \(x^2-5x-6 > 0\)
4. \(x^2-x-2 < 0\)

Langkah-langkah menyelesaikan pertidaksamaan kuadrat

Pada umumnya, untuk mencari himpunan penyelesaian pertidaksamaan kuadrat kita dapat mengikuti langkah-langkah sebagai berikut:

Langkah 1: Tentukan pembuat nol yakni dengan mengubah tanda pertidaksamaan menjadi tanda "sama dengan" sehingga terbentuklah suatu persamaan kuadrat. Akar-akar persamaan kuadrat yang diperoleh adalah pembuat nol.

Langkah 2: Lukiskan pembuat nol pada suatu garis bilangan, lalu tentukan tanda untuk masing-masing interval dengan memasukkan sembarang bilangan yang terletak pada tiap-tiap interval ke persamaan pada ruas kiri persamaan kuadrat yang diperoleh dari Langkah 1. Kemudian, tuliskan tanda (+) jika hasil substitusi bernilai positif dan (-) jika hasil substitusi bernilai negatif.

Langkah 3: Tentukan daerah penyelesaian.

Untuk pertidaksamaan ">" atau "≥", daerah penyelesaian berada pada interval dengan tanda (+). Sedangkan untuk pertidaksamaan "<" atau "≤", daerah penyelesaian berada pada interval dengan tanda (-).

Langkah 4: Tuliskan himpunan penyelesaiannya, yakni interval yang memuat daerah penyelesaian.

Setelah memahami langkah-langkah di atas, mari kita selesaikan pertidaksamaan pada contoh soal berikut.

Contoh 1:

Tentukan himpunan penyelesaian dari pertidaksamaan \( x^2-x-12 \geq 0 \).

Pembahasan:

Langkah 1: Tentukan pembuat nol dari pertidaksamaan sehingga terbentuk pertidaksamaan kuadrat yakni \( x^2-x-12 = 0 \). Dengan cara pemfaktoran, kita peroleh akar-akar persamaan kuadrat tersebut, yaitu:

Langkah 2: Lukiskan pembuat nol pada garis bilangan dengan batas seperti pada Gambar 1 berikut.

Gambar 1. Pembuat nol pada garis bilangan

Selanjutnya, tentukan tanda dari masing-masing daerah pada garis bilangan tersebut. Kita ambil sembarang bilangan atau titik uji yang terletak pada tiap-tiap interval yakni \(x = -4, \ x = 0\), dan \(x = 5\), kemudian substitusikan nilai titik uji tersebut ke persamaan kuadrat \( x^2-x-12 \). Kita peroleh:

\begin{aligned} \text{Untuk} \ x = -4, \ \text{maka} \\[8pt] x^2-x-12 &= (-4)^2 - (-4) - 12 = 8 \\[8pt] \text{Untuk} \ x = 0, \ \text{maka} \\[8pt] x^2-x-12 &= 0^2 - 0 - 12 = -12 \\[8pt] \text{Untuk} \ x = -4, \ \text{maka} \\[8pt] x^2-x-12 &= 5^2 - 5 - 12 = 8 \end{aligned}

Perhatikan bahwa untuk \(x = 0\) menghasilkan nilai negatif sehingga daerah yang memuat angka nol, daerahnya adalah bertanda negatif. Sedangkan untuk \(x = -4\) dan \(x = 5\) menghasilkan nilai positif sehingga daerahnya bertanda positif. Perhatikan Gambar 2 berikut:

Gambar 2. Pembuat nol pada garis bilangan dan tanda untuk masing-masing interval

Langkah 3: Karena bentuk pertidaksamaan adalah "≥", maka daerah penyelesaiannya berada pada interval dengan tanda (+). Dari Gambar 2, terlihat bahwa himpunan penyelesaian pertidaksamaan kuadrat yang memenuhi adalah:

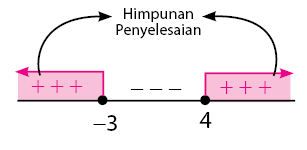
Gambar 3. Daerah himpunan penyelesaian pertidaksamaan

Langkah 4: Berdasarkan hasil di atas, maka himpunan penyelesaian dari pertidaksamaan kuadrat \( x^2-x-12 \geq 0 \) adalah \(x \leq -3\) dan \( x \geq 4 \).

Contoh 2:

Himpunan penyelesaian dari pertidaksamaan kuadrat \( x^2-8x+15 \leq 0 \) untuk \(x \in R\) adalah…

1. \( \{ x | -5 \leq x \leq -3 \} \)
2. \( \{ x | 3 \leq x \leq 5 \} \)
3. \( \{ x | x \leq -5 \ \text{atau} \ x \geq -3 \} \)
4. \( \{ x | x \leq -3 \ \text{atau} \ x \geq 5 \} \)
5. \( \{ x | x \leq -3 \ \text{atau} \ x \geq -5 \} \)

Pembahasan »

Untuk menyelesaikan soal ini kita bisa faktorkan pertidaksamaan kuadrat di atas. Perhatikan berikut ini:

\begin{aligned} x^2-8x+15 &\leq 0 \\[8pt] (x-3)(x-5) &\leq 0 \\[8pt] x = 3 \ &\text{atau} \ x = 5 \end{aligned}

Selanjutnya, dari hasil di atas kita buat garis bilangannya seperti pada gambar di bawah.

Karena notasi pertidaksamaan kurang dari sama dengan \( (\leq) \), maka himpunan penyelesaiannya ditunjukkan oleh garis bilangan bertanda negatif atau pada interval \( 3 \leq x \leq 5 \).

Jawaban B.

Contoh 3:

Himpunan penyelesaian dari pertidaksamaan kuadrat \(x^2-5x-6 > 0\) untuk \(x \in R\) adalah…

1. \( \{ x | x < -1 \ \text{atau} \ x > 6 \} \)
2. \( \{ x | x < 2 \ \text{atau} \ x > 3 \} \)
3. \( \{ x | -3 < x < 2 \} \)
4. \( \{ x | x < -6 \ \text{atau} \ x > 6 \} \)
5. \( \{ x | -6 < x < 1 \} \)

Pembahasan »

Untuk menyelesaikan soal ini, kita bisa faktorkan bentuk pertidaksamaan kuadratnya, yakni:

\begin{aligned} x^2-5x-6 &> 0 \\[8pt] (x-6)(x+1) &> 0 \\[8pt] x = 6 \ &\text{atau} \ x = -1 \end{aligned}

Selanjutnya, dari hasil di atas kita bisa buat garis bilangannya seperti pada gambar di bawah.

Karena notasi pertidaksamaan pada soal di atas adalah lebih dari (>), maka himpunan penyelesaian ditunjukkan oleh garis bilangan dengan tanda positif atau pada interval \( \{ x|x < -1 \ \text{atau} \ x > 6 \} \).

Jawaban A.

Contoh 4: UM UNDIP 2019

Solusi dari pertidaksamaan \( 2x(x+1) > (x+1)(x+2) \) adalah…

1. \( x > 2 \)
2. \( -1 < x < 2 \)
3. \( -2 < x < 1 \)
4. \( x < -1 \ \text{atau} \ x > 2 \)
5. \( x < -2 \ \text{atau} \ x > 1 \)

Pembahasan »

Untuk menyelesaikan bentuk pertidaksamaan di atas, kita bisa sederhanakan bentuknya sampai ke bentuk umum pertidaksamaan kuadrat, yakni:

\begin{aligned} 2x(x+1) &> (x+1)(x+2) \\[8pt] 2x^2+2x &> x^2+2x+x+2 \\[8pt] 2x^2+2x &> x^2+3x+2 \\[8pt] 2x^2-x^2+2x-3x-2 &>0 \\[8pt] x^2-x-2 &> 0 \\[8pt] (x-2)(x+1) &> 0 \\[8pt] x = 2 \ &\text{atau} \ x = -1 \end{aligned}

Selanjutnya, dari hasil yang diperoleh di atas, kita peroleh garis bilangannya seperti berikut ini:

Dari hasil di atas kita peroleh himpunan penyelesaian pertidaksamaan kuadrat yang diberikan dalam soal adalah \( x < -1 \) atau \(x > 2 \).

Jawaban D.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.