Matematika Dasar   »   Rumus-rumus Segitiga   ›  Aturan Sinus dalam Suatu Segitiga

Aturan Sinus

Aturan Sinus dalam Suatu Segitiga

Aturan Sinus menjelaskan hubungan antara perbandingan panjang sisi yang berhadapan dengan suatu sudut terhadap sinus sudut tersebut pada suatu segitiga.

Oleh Tju Ji Long · Statistisi

Hub. WA: 0812-5632-4552

Aturan Sinus menjelaskan hubungan antara perbandingan panjang sisi yang berhadapan dengan suatu sudut terhadap sinus sudut tersebut pada suatu segitiga. Melalui aturan sinus ini kita dapat mengetahui panjang sisi atau besarnya sudut pada suatu segitiga sembarang. Supaya lebih jelas, perhatikan gambar segitiga ABC berikut ini.

Gambar 1. Segitiga aturan sinus

Pada \(ΔABC\), ditarik garis tinggi \(\overline{BD}\) dan \(\overline{AE}\).

Pada \(ΔABD\) berlaku

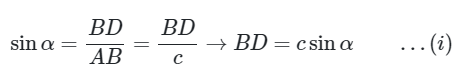
Pada \(ΔCBD\) berlaku

Dari persamaan (i) dan (ii), diperoleh:

Pada \(ΔCAE\) berlaku

Pada \(ΔABE\) berlaku

Dari persamaan (iii) dan (iv) diperoleh

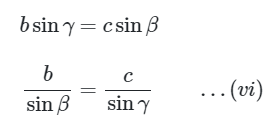
Dengan demikian, dari persamaan (iii) dan (vi), diperoleh

Persamaan terakhir ini disebut aturan sinus dalam suatu segitiga. Supaya lebih jelas, perhatikanlah beberapa contoh berikut ini.

Contoh 1:

Diketahui ΔABC dengan besar sudut dan panjang sisi-sisinya seperti tampak pada Gambar di bawah. Tentukanlah nilai b, c, dan besar sudut C!

Pembahasan:

Nilai \(a, \ b\), dan \(∠C\) dapat ditentukan dengan menggunakan aturan sinus maka:

Besar sudut C adalah

Sehingga panjang sisi \(b\) adalah

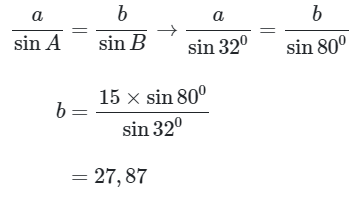
dan panjang sisi \(c\) adalah

Contoh 2:

Suatu segitiga ABC memiliki panjang \(AC = 10\) cm. Jika besar \(∠BAC=45^0\) dan \(∠ABC=60^0\), maka berapakah panjang BC?

Pembahasan:

Berdasarkan informasi yang diberikan pada soal diperoleh informasi seperti berikut.

Dengan demikian, kita peroleh

Jadi, panjang BC adalah \( \frac{10\sqrt{6}}{3} \) cm.

Cukup sekian penjelasan mengenai aturan sinus dalam artikel ini. Semoga bermanfaat.

Sumber:

Sunardi, Slamet Waluyo & Sutrisna. 2014. Konsep dan Penerapan Matematika SMA/MA Kelas XI. Jakarta: Penerbit PT Bumi Aksara.

Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.