Matematika Dasar   »   Matriks   ›  Menghitung Determinan Matriks

Matriks

Menghitung Determinan Matriks

Determinan matriks 2 x 2 dapat diperoleh dengan mengalikan entri-entri pada diagonal utama dan mengurangkan hasil kali entri-entri pada diagonal lainnya.

Oleh Tju Ji Long · Statistisi

Hub. WA: 0812-5632-4552

Pada artikel sebelumnya, kita telah membahas mengenai matriks mulai dari notasi, sifat-sifat hingga operasi yang umum dalam matriks. Pada artikel ini kita akan teruskan materi tersebut dengan mendefinisikan apa itu determinan matriks dan bagaimana mencari determinan matriks berukuran 2 x 2 dan 3 x 3.

Determinan dari suatu matriks persegi A dinotasikan dengan:

Apabila matriks A berordo 2 x 2 , yaitu

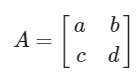
maka determinan dari matriks \(A\) didefinisikan sebagai

Adapun untuk matriks berordo 3 x 3, misal

maka determinan matriks B didefinisikan sebagai:

Untuk memudahkan teman-teman dalam mengingat rumus di atas perhatikanlah ilustrasi berikut.

Ilustrasi (a) memperlihatkan bahwa determinan matriks \(2×2\) dapat diperoleh dengan mengalikan entri-entri pada panah yang mengarah ke kanan dan mengurangkan hasil kali entri-entri pada panah yang mengarah ke kiri.

Sementara pada ilustrasi (b), kita menyalin kembali kolom pertama dan kolom kedua; kemudian menyandingkannya ke sebelah kanan matriks tersebut. Determinan matriks \(3×3\) tersebut kemudian dihitung dengan menjumlahkan hasil kali pada panah-panah yang mengarah ke kanan dan mengurangkan hasil kali pada panah-panah yang mengarah ke kiri.

Perhatikan contoh soal berikut:

Contoh 1: Determinan Matriks 2 x 2

Tentukan determinan dari matriks berukuran 2 x 2 berikut ini.

Pembahasan:

Dengan menggunakan rumus determinan yang telah kita pelajari, diperoleh

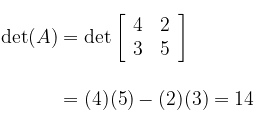
Jadi, determinan matriks A adalah 14.

Contoh 2: Determinan Matriks 2 x 2

Diketahui matriks A seperti di bawah ini.

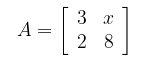
Jika determinan dari matriks A adalah 18, tentukan nilai x.

Pembahasan:

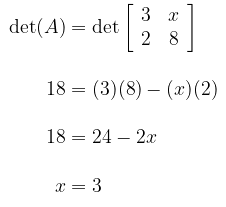
Jadi, nilai \(x\) yaitu 3.

Contoh 3: Determinan Matriks 3 x 3

Tentukanlah determinan dari matriks berukuran 3 x 3 berikut ini.

Pembahasan:

Cukup sekian penjelasan mengenai cara mencari determinan matriks 2 x 2 dan 3 x 3 dalam artikel ini. Semoga bermanfaat.

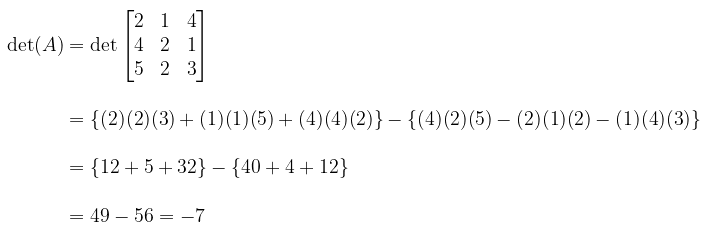
Sumber:

Sunardi, Slamet Waluyo & Sutrisna. 2014. Konsep dan Penerapan Matematika SMA/MA Kelas XI. Jakarta: Penerbit PT Bumi Aksara.

Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.

Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.