www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Rumus-rumus Segitiga › Luas Segitiga dengan Aturan Trigonometri
Luas Segitiga dengan Aturan Trigonometri
Pada umumnya, luas suatu segitiga dapat diperoleh dengan mengalikan alas dan tinggi dari segitiga tersebut dan kemudian membaginya dengan 2. Namun, terdapat cara lain untuk menghitung luas segitiga yakni dengan menggunakan rumus aturan trigonometri.
Jika kamu butuh bantuan guru, mungkin kamu bisa pertimbangkan les matematika bersama Superprof: Les Privat Matematika dengan Guru-guru Terbaik.
Sebagaimana telah kita pelajari bahwa luas suatu segitiga dapat diperoleh dengan mengalikan alas dan tinggi dari segitiga tersebut dan kemudian membaginya dengan 2, atau dapat dituliskan sebagai

Selain menggunakan rumus di atas, luas segitiga tersebut juga dapat diperoleh dengan menggunakan rumus aturan trigonometri.
Sekarang amatilah segitiga ABC berikut!

Gambar 1. Segitiga ABC dengan sudut dan sisi-sisinya
Perhatikan bahwa segitiga ABC pada Gambar 1 terbagi lagi menjadi dua segitiga yakni \(ΔADC\) dan \(ΔBDC\). Pada \(ΔADC\), kita peroleh

Dengan demikian,
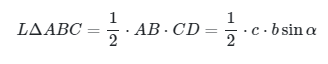
Jadi, luas \( L ΔABC \) dapat dinyatakan sebagai

Dengan cara yang sama, untuk setiap segitiga ABC juga berlaku:
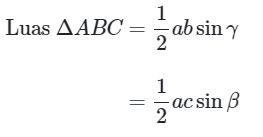
Contoh 1:
Tentukan luas segitiga ABC pada Gambar 1 di atas jika diketahui sisi \(BC = 4\) cm, \(AC = 7\sqrt{3}\) cm dan \(∠C=60^0\).
Pembahasan:
Diketahui \(BC = a = 4\) cm; \(AC = b = 7\sqrt{3}\) dan \(∠C=60^0\). Dengan demikian, kita peroleh

Contoh 2:
Sebuah segitiga ABC diketahui luasnya 18 cm2. Jika panjang sisi \(BC = 4\) cm dan \(AB = 6\sqrt{3}\) cm, maka tentukanlah besar sudut B.
Pembahasan:
Diketahui luas segitiga = 18, \(BC = a = 4\); dan \(AB = c = 6\sqrt{3}\). Dengan demikian, kita peroleh

Luas Segitiga Jika Hanya Diketahui Panjang Ketiga Sisinya
Dari Gambar 1, jika diketahui hanya nilai ketiga sisinya maka luas segitiga ABC dapat juga ditentukan dengan rumus berikut.

di mana: \( S = \frac{1}{2} (a + b + c) \).
Bukti:
Menurut identitas trigonometri diketahui bahwa

Jika persamaan (2) disubstitusikan ke (1) maka diperoleh:

di mana: \( S = \frac{1}{2} (a + b + c) \).
Contoh 3:
Hitunglah luas segitiga ABC jika diketahui panjang sisi-sisinya a = 16 cm, b = 14 cm, dan c = 10 cm!
Pembahasan:
Pertama, kita hitung

Sehingga luas segitiga ABC adalah

Jadi, luas segitiga ABC adalah \(40\sqrt{3}\) cm2.
Cukup sekian penjelasan mengenai cara mencari luas segitiga menggunakan aturan trigonometri dalam artikel ini. Jika kamu ingin belajar subjek lain, kamu bisa cek Blog Edukatif Superprof.
Sumber:
Sunardi, Slamet Waluyo & Sutrisna. 2014. Konsep dan Penerapan Matematika SMA/MA Kelas XI. Jakarta: Penerbit PT Bumi Aksara.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Don't let yesterday take up too much of today.
