www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar
Relasi dan Fungsi
Bentuk Pangkat, Akar dan Logaritma
Persamaan Polinomial
Pertidaksamaan
Limit Fungsi
Turunan Fungsi
Integral
Matriks
Sistem Persamaan Linear
Barisan dan Deret
Statistika
Trigonometri
Geometri
Rumus-rumus Segitiga
Lingkaran
Matematika Dasar » Geometri › Bangun Datar
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Geometri
Bangun Datar
Beberapa bangun datar yang akan kita pelajari yakni persegi, persegi panjang, segitiga, jajar genjang, trapesium, layang-layang, belah ketupat, dan lingkaran. Pada tiap-tiap bangun tersebut dapat dihitung luas dan kelilingnya.
Oleh Tju Ji Long · Statistisi
Hub. WA: 0812-5632-4552
Bangun datar dapat didefinisikan sebagai suatu bidang datar yang tersusun oleh titik-titik atau garis-garis yang menyatu sehingga membentuk bangun dua dimensi.
Terdapat beberapa bangun datar yang akan kita pelajari yakni persegi, persegi panjang, segitiga, jajar genjang, trapesium, layang-layang, belah ketupat, dan lingkaran. Pada tiap-tiap bangun tersebut dapat dihitung luas dan kelilingnya.
Pada artikel ini, kita akan mempelajari rumus-rumus untuk menghitung luas dan keliling serta sifat-sifat yang dimiliki oleh bangun datar tersebut.
Persegi
Persegi adalah bangun datar dua dimensi yang dibentuk oleh empat sisi yang sama panjang dan keempat titik sudutnya membentuk sudut siku-siku (900).
Perhatikan gambar persegi berikut ini.
Gambar 1. Persegi dengan ukuran berbeda
Luas dan keliling dari suatu persegi diberikan oleh
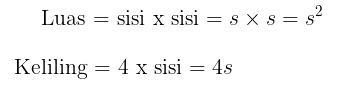
Contoh 1:
Suatu persegi memiliki panjang sisi 5 cm. Tentukanlah luas dan kelling persegi tersebut.
Pembahasan:
Luas dan keliling persegi tersebut adalah
Persegi Panjang
Persegi panjang merupakan bangun datar atau bidang yang mempunyai sisi berhadapan yang sama panjang dan memiliki empat buah titik sudut siku-siku.
Perhatikan gambar persegi panjang berikut ini.
Gambar 2. Persegi panjang
Luas dan keliling dari persegi panjang dapat diperoleh dengan rumus berikut:
Contoh 2:
Suatu persegi panjang ABCD memiliki panjang 8 cm dan lebar 5 cm. Tentukanlah:
- Luas persegi panjang ABCD.
- Keliling persegi panjang ABCD.
Pembahasan:
- Luas persegi panjang ABCD tersebut adalah
- Keliling persegi panjang ABCD adalah
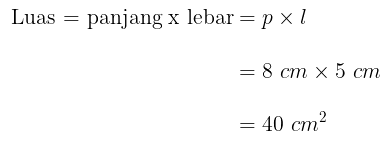
Segitiga
Segitiga merupakan bangun datar dua dimensi yang dibentuk oleh tiga sisi berupa garis lurus dan memiliki tiga sudut dengan besar sudut 1800.
Berdasarkan panjang sisinya, bangun datar segitiga dapat dibedakan menjadi tiga yaitu segitiga sama sisi, segitiga sama kaki, dan segitiga sembarang.
Perhatikan gambar segitiga berikut ini.
Luas dan keliling dari segitiga dapat diperoleh dengan rumus berikut:
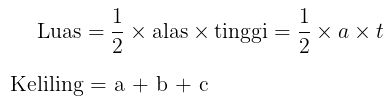
Contoh 3:
Perhatikan gambar segitiga di bawah
Tentukanlah luas dan keliling segitiga tersebut.
Pembahasan:
Perhatkan bahwa segitiga BAC merupakan segitiga siku-siku dengan sudut A = 90 derajat. Dengan demikian, salah satu kaki sudutnya bisa dijadikan tinggi atau alas segitiga tersebut. Luas segitiga tersebut adalah
Keliling segitiga BAC merupakan penjumlahan dari panjang ketiga sisinya yakni
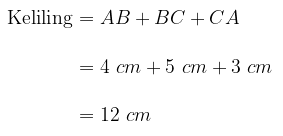
Jajar Genjang
Jajar genjang merupakan bangun datar dua dimensi yang memiliki dua pasang sisi yang sama panjang dan sejajar serta mempunyai dua pasang sudut yang sama besar yakni pasangan sudut lancip dan pasangan sudut tumpul.
Perhatikan gambar jajar genjang berikut ini.
Luas dan keliling dari jajar genjang dapat diperoleh dengan rumus berikut:
Contoh 4:
Perhatikan gambar jajar genjang ABCD di bawah ini.
Jika BC = DA = 8 cm. Tentukan luas dan keliling jajar genjang ABCD tersebut.
Pembahasan:
Informasi untuk menghitung luas telah tersedia pada gambar di atas yakni jajar genjang mempunyai alas = 8 cm dan tinggi 7 cm. Sehingga luasnya adalah
Keliling jajar genjang ABCD merupakan penjumlahan dari panjang sisi-sisinya yakni
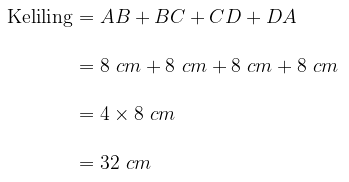
Trapesium
Trapesium merupakan bangun datar dua dimensi yang memiliki empat sisi di mana dua sisinya saling sejajar yang tidak sama panjang serta mempunyai minimal satu titik sudut tumpul. Trapesium dapat dibedakan menjadi trapesium sembarang, trapesium sama kaki, dan trapesium siku-siku.
Perhatikan gambar trapesium berikut ini.
Luas dan keliling dari trapesium dapat diperoleh dengan rumus berikut:
Contoh 5:
Misalkan diketahui trapesium seperti tampak pada gambar di bawah
Hitunglah luas dan keliling trapesium tersebut.
Pembahasan:
Informasi untuk menghitung luas dan keliling trapesium telah ditunjukkan pada gambar di atas. Dengan demikian, luas dan kelilingnya adalah
Catatan: panjang BC = AD diperoleh dari teorema pythagoras, yakni
Layang-layang
Layang-layang adalah bangun datar dua dimensi yang dibentuk oleh dua pasang sisi sama panjang yang saling membentuk sudut yang berbeda.
Perhatikan gambar layang-layang berikut ini.
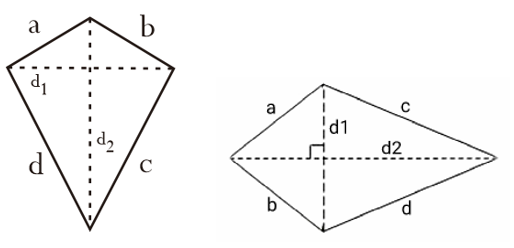
Luas dan keliling dari layang-layang dapat diperoleh dengan rumus berikut:
Contoh 6:
Perhatikan layang-layang ABCD di bawah ini
Carilah luas dan keliling layang-layang tersebut.
Pembahasan:
Luas layang-layang ABCD di atas adalah
dan kelilingnya adalah
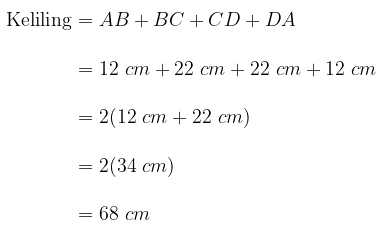
Belah Ketupat
Belah ketupat adalah bangun datar dua dimensi yang dibentuk oleh empat buah sisi yang sama panjang dan mempunyai dua pasang sudut bukan siku-siku dengan sudut yang saling berhadapan mempunyai besar yang sama.
Perhatikan gambar belah ketupat berikut ini.
Luas dan keliling dari belah ketupat dapat diperoleh dengan rumus berikut:
Contoh 7:
Perhatikan gambar belah ketupat di bawah ini.
Tentukan luas dan keliling dari belah ketupat ABCD tersebut.
Pembahasan:
Informasi untuk menghitung luas dan kelilingnya telah diberikan pada gambar di atas. Kita peroleh
Lingkaran
Lingkaran adalah bangun datar dua dimensi yang dibentuk oleh himpunan semua titik yang mempunyai jarak sama dari suatu titik tetap yang disebut pusat lingkaran.
Perhatikan gambar lingkaran berikut ini.
Luas dan keliling dari lingkaran dapat diperoleh dengan rumus berikut:
Contoh 8:
Diketahui suatu lingkaran memiliki panjang diameter 14 cm. Tentukanlah luas dan keliling lingkaran tersebut.
Pembahasan:
Ingat bahwa diameter lingkaran sama dengan dua kali jari-jarinya (r) sehingga r = 7 cm. Karena r merupakan kelipatan 7 maka kita gunakan \( \pi = 22/7 \). (Jika r bukan kelipatan 7 kita gunakan \( \pi = 3,14 \)).
Luas lingkarannya adalah
Keliling lingkarannya adalah
Cukup sekian penjelasan mengenai bangun datar atau bangun dua dimensi dalam artikel ini. Semoga bermanfaat.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
It is our choices that show what we truly are, far more than our abilities.