www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Fungsi Trigonometri › Menyelesaikan Persamaan Trigonometri
Menyelesaikan Persamaan Trigonometri
Salah satu pembahasan penting dalam trigonometri berkaitan dengan mencari himpunan penyelesaian dari suatu persamaan trigonometri yang terdiri atas sudut-sudut yang memenuhi persamaan trigonometri tersebut.
Salah satu pembahasan penting dalam trigonometri berkaitan dengan mencari solusi atau himpunan penyelesaian dari suatu persamaan trigonometri. Himpunan penyelesaian dari persamaan trigonometri terdiri atas sudut-sudut yang memenuhi persamaan trigonometri tersebut.
Anda mungkin masih ingat bahwa bentuk grafik fungsi trigonometri adalah bersifat periodik, yakni bentuknya berulang sama pada rentang tertentu. Oleh karena itu, sudut yang memenuhi persamaan fungsi trigonometri tidak hanya mempunyai nilai tunggal (kecuali jika sudutnya dibatasi sehingga hanya terdapat satu nilai tunggal yang memenuhi). Dengan kata lain, terdapat sudut-sudut berbeda yang membuat fungsi trigonometri tersebut bernilai sama.
Sebagai contoh, perhatikan fungsi \( \sin x = \frac{1}{2} \). Di sini, nilai \(x\) atau sudut yang memenuhi tidak hanya 300 sebagaimana yang telah kita ketahui bahwa \( \sin 30^0 = \frac{1}{2} \). Nilai \(x\) lain yang juga memenuhi adalah \(x = 150^0\). Lantas, bagaimana mencari semua nilai \(x\) yang memenuhi fungsi tersebut? Pada artikel ini, kita akan membahas berbagai cara untuk menemukan nilai \(x\) tersebut.
Pada umumnya, terdapat lima jenis persamaan trigonometri yang sering muncul, yakni
- \( \sin x = \sin \alpha \)
- \( \cos x = \cos \alpha \)
- \( \tan x = \tan \alpha \)
- \( a \cos x + b \sin x = c \)
- \( A \sin^2 x + B \sin x + C = 0 \)
Kita akan membahas kelima jenis persamaan trigonometri tersebut.
#1. \(\sin x = \sin \alpha\)
Grafik fungsi sinus bersifat periodik dan membentuk bukit dan lembah. Oleh karena itu, nilai fungsi sinus untuk besar satu sudut tertentu akan sama dengan nilai fungsi untuk besar sudut yang lain. Nilai untuk fungsi sinus dimulai dari nol dan kembali ke nol. Nilai tertinggi fungsi y = sin x adalah 1 dan nilai terendahnya adalah -1.
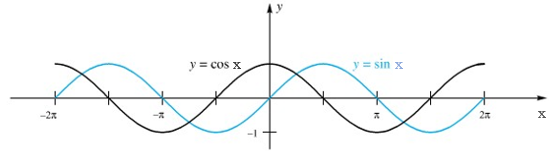
Gambar 1. Fungsi sinus dan cosinus
Himpunan penyelesaian untuk persamaan \(\sin x = \sin \alpha\) dapat dinyatakan sebagai berikut.
| Dalam derajat | Dalam radian |
|---|---|
 |  |
di mana k adalah bilangan bulat (k = 0, 1, 2, 3, ... ).
Contoh 1:
Tentukanlah himpunan penyelesaian dari \( \sin x = \frac{1}{2} \) untuk \( 0^0 \leq x \leq 360^0 \).
Pembahasan:
Kita tahu bahwa \( \sin 30^0 = \frac{1}{2} \) sehingga kita peroleh persamaan berikut
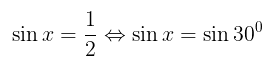
Sebagaimana dinyatakan di atas bahwa himpunan penyelesaian untuk persamaan ini dapat dinyatakan dalam derajat dan dalam radian. Kita akan pelajari keduanya.
Dalam Derajat
Himpunan penyelesaiannya adalah

Perhatikan bahwa nilai \(k\) yang memenuhi adalah \(k = 0\) saja, karena untuk \(k\) yang lebih besar akan membuat \( x_1 \) dan \( x_2 \) lebih besar dari 3600 yang mana melanggar syarat yang diberikan dalam soal.
Jadi, himpunan penyelesaiannya adalah: HP = {300, 1500}.
Dalam Radian
Sebenarnya, himpunan penyelesaian dalam radian tidak jauh berbeda dengan himpunan penyelesaian dalam derajat. Hanya saja kita nyatakan dalam radian saja. Kita tahu bahwa \( \pi = 180^0 \) dan \( \sin 30^0 = \sin \frac{\pi}{6} = \frac{1}{2} \) sehingga kita peroleh persamaan berikut.
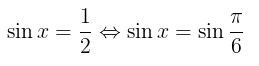
Adapun himpunan penyelesaiannya yaitu
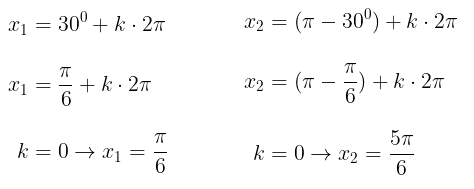
Jadi, himpunan penyelesaiannya adalah:

Perhatikan bahwa untuk mencari himpunan penyelesaian dalam bentuk radian, kita tidak perlu melakukan perhitungan dari awal seperti yang kita lakukan pada Contoh 1. Kita cukup memanfaatkan hasil himpunan penyelesaian dalam derajat yakni HP = {300, 1500} dan memanfaatkan kenyataan bahwa \( \pi = 180^0 \). Kita tahu bahwa

Sehingga himpunan penyelesaian dalam radian yaitu

#2. \( \cos x = \cos \alpha \)
Grafik fungsi cosinus juga bersifat periodik dan membentuk bukit dan lembah. Hanya saja, pada fungsi y = cos x dimulai dari satu dan kembali ke satu. Nilai tertinggi untuk y = cos x adalah 1 dan nilai terendahnya adalah -1. Grafik fungsi cosinus dapat dilihat pada Gambar 1 di atas.
Himpunan penyelesaikan persamaan trigonometri untuk fungsi cosinus dinyatakan sebagai berikut.
| Dalam derajat | Dalam radian |
|---|---|
 | 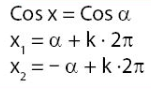 |
di mana k adalah bilangan bulat (k = 0, 1, 2, 3, ... ).
Contoh 2:
Tentukan himpunan penyelesaian dari \( \cos x = \frac{1}{2} \) untuk \( 0^0 \leq x \leq 360^0 \).
Pembahasan:
Kita tahu bahwa \( \cos 60^0 = \frac{1}{2} \) sehingga kita peroleh persamaan berikut
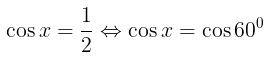
Himpunan penyelesaiannya adalah
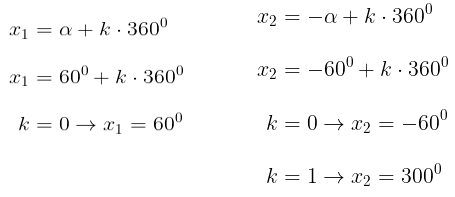
Perhatikan bahwa \( x_2 = -60^0 \) bukan himpunan penyelesaian karena tidak memenuhi syarat yang diberikan dalam soal. Dengan demikian, himpunan penyelesaian dari \( \cos x = \frac{1}{2} \) untuk \( 0^0 \leq x \leq 360^0 \) adalah HP = {600, 3000}
Selain itu, kita tahu bahwa

Jadi, himpunan penyelesaian dalam bentuk radiannya adalah

#3. \( \tan x = \tan \alpha \)
Grafik fungsi tangen berbeda dengan grafik fungsi sinus dan cosinus yang membentuk bukit dan lembah seperti yang telah kita bahas di atas. Hal ini disebabkan nilai tangen yang tidak terdefinisi pada besar sudut -2700, -900, 900 dan 2700. Oleh karena itu, dalam rentang 0 sampai 360 derajat akan terdapat empat buah asimtot.
Himpunan penyelesaikan persamaan trigonometri untuk fungsi tangen dinyatakan sebagai berikut.
| Dalam derajat | Dalam radian |
|---|---|
 | 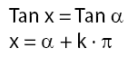 |
di mana k adalah bilangan bulat (k = 0, 1, 2, 3, ... ).
Contoh 3:
Tentukan himpunan penyelesaian dari \( \tan x = \sqrt{3} \) untuk \( 0^0 \leq x \leq 360^0 \).
Pembahasan:
Kita tahu bahwa \( \tan 60^0 = \sqrt{3} \) sehingga kita peroleh persamaan berikut

Himpunan penyelesaiannya

Jadi, himpunan penyelesaiannya dalam derajat adalah HP = {600, 2400}
Karena

Maka himpunan penyelesaian dalam radian yaitu

#4. \( a \cos x + b \sin x = c \)
Untuk menyelesaikan persamaan trigonometri bentuk ini, ubahlah persamaan sehingga menjadi
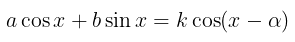
di mana:

Contoh 4:
Himpunan penyelesaian persamaan
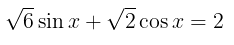
untuk \( 0 \leq x \leq 360^0 \) adalah...
Pembahasan:
Perhatikan bahwa

Misalkan bahwa

Dengan demikian, kita peroleh
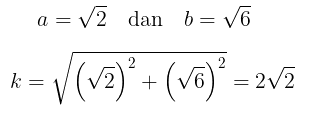
Karena \((a,b) = ( \sqrt{2}, \sqrt{6} )\) berada di kuadran I, maka \( \theta \) juga berada di kuadran I. Kita peroleh

Jadi, kita peroleh persamaan berikut:
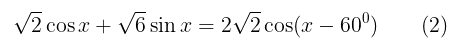
Dari persamaan (1) dan (2), diperoleh hubungan
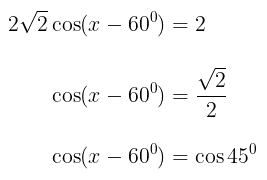
Solusi 1:
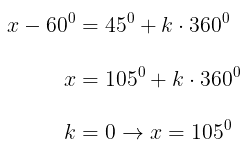
Solusi 2:
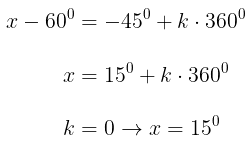
Jadi, himpunan penyelesaiannya adalah HP = { 150, 1050 }.
#5. \( A \sin^2 x + B \sin x + C = 0 \)
Kita dapat menyelesaian persamaan trigonometri bentuk ini seperti menyelesaikan persamaan kuadrat.
Contoh 5:
Himpunan penyelesaian dari persamaan trigonometri \( \cos 2x + \sin x = 0 \) untuk \( 0 \leq x \leq 360^0 \) adalah...
Pembahasan:
Perhatikan bahwa kita dapat mengubah persamaan \( \cos 2x + \sin x = 0 \) ke dalam bentuk persamaan kuadrat yaitu

Perhatikan bahwa untuk \( \sin x = -1/2; \ 0 \leq x \leq 360 \), kita peroleh \( x = 210^0 \) dan \( x = 330^0 \) sehingga himpunan penyelesaiannya adalah HP = { 2100, 3300 }. (Perhitungan tidak ditunjukkan di sini. Anda bisa mencarinya dengan merujuk pada Contoh 1).
Sementara itu, untuk \( \sin x = 1; \ 0 \leq x \leq 360 \), kita peroleh \( x = 90^0 \) sehingga himpunan penyelesaiannya adalah HP = {900}.
Dengan menggabungkan himpunan penyelesaian untuk \( \sin x = -1/2 \) dan \( \sin x = 1 \), kita peroleh himpunan penyelesaian untuk persamaan trigonometri \( \cos 2x + \sin x = 0 \) yaitu
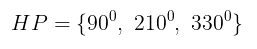
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Use your time wisely, because time will never get back.
