www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Rumus-rumus Segitiga › Aturan Cosinus dalam Suatu Segitiga
Aturan Cosinus dalam Suatu Segitiga
Bila panjang dua sisi segitiga dan sudut yang diapit oleh kedua sisi tersebut diketahui, maka panjang sisi segitiga yang satunya dapat ditentukan dengan aturan cosinus.
Pada artikel sebelumnya kita telah belajar mengenai aturan sinus. Dengan aturan tersebut, kita bisa menentukan panjang sisi dan besar sudut dalam sebuah segitiga sembarang. Hal ini berlaku jika diketahui panjang dua sisi dan satu sudut di hadapan salah satu sisi segitiga tersebut atau jika diketahui dua sudut dan panjang satu sisi di hadapan salah satu sudut segitiga.
Namun, jika pada sebuah segitiga hanya diketahui dua sisi dan sebuah sudut yang diapit oleh kedua sisi tersebut maka aturan sinus tidak dapat digunakan untuk menentukan panjang sisi dan besar sudut lainnya dalam suatu segitiga sembarang. Dalam hal ini kita dapat menggunakan aturan kosinus.
Supaya lebih jelas, amati Gambar 1 berikut ini. Tampak bahwa ΔABC terdiri dari ΔADC dan ΔBDC.
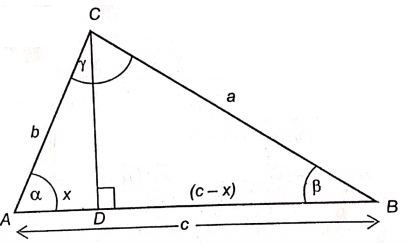
Gambar 1. Segitiga aturan cosinus
Perhatikan bahwa:
Pada \(ΔABC\), jika \(AD = x\) maka \(BD = c – x\).
Pada ΔADC berlaku

Pada \(ΔBDC\) berlaku

Dari persamaan (i) dan (ii) diperoleh hubungan:

Pada \(ΔADC\), kita peroleh

Dengan substitusikan (iv) ke (iii) maka

Persamaan terakhir ini merupakan salah satu aturan kosinus. Aturan kosinus lainnya pada ΔABC dapat diperoleh dengan cara yang sama, sehingga

Jadi, secara umum, pada setiap ΔABC berlaku aturan kosinus:
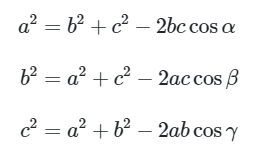
Perhatikanlah bahwa bila panjang dua sisi sebuah segitiga dan sudut yang diapit oleh kedua sisi tersebut diketahui, maka kita dapat menentukan panjang sisi yang satunya berdasarkan rumus di atas. Sebaliknya, jika panjang dari tiga sisi diketahui, kita dapat menentukan besar sudut dalam segitiga tersebut dengan mengubah sedikit aturan kosinus tadi, yakni

Untuk lebih memahami tentang aturan kosinus ini, perhatikan contoh soal berikut.
Contoh 1:
Pada segitiga ABC seperti tampak pada gambar di bawah, diketahui \(∠A=60^0, \ b=10\) cm, dan \(c=16\) cm. Hitunglah panjang sisi \(a\).
Pembahasan:

Jadi, \(a = 14\) cm.
Contoh 2:
Pada suatu segitiga dengan sisi-sisi a, b, dan c memenuhi \(a^2-b^2=c^2-bc\). Tentukanlah besar sudut A.
Pembahasan:
Diketahui \(a^2-b^2=c^2-bc\) sehingga dapat diperoleh \(a^2=b^2+c^2-bc\). Dari aturan cosinus diketahui juga bahwa \(a^2=b^2+c^2-2bc⋅ \cos A\). Dengan menyelesaikan dua persamaan di atas, maka akan diperoleh nilai \(\cos A\), yakni

Sumber:
Sunardi, Slamet Waluyo & Sutrisna. 2014. Konsep dan Penerapan Matematika SMA/MA Kelas XI. Jakarta: Penerbit PT Bumi Aksara.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
Hanya satu cara menghindari kritikan: tidak berbuat apa-apa, tidak berkata apa-apa, dan tidak menjadi apa-apa.
