
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Limit Fungsi › Limit Trigonometri, Contoh Soal dan Pembahasan
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Limit Trigonometri, Contoh Soal dan Pembahasan
Konsep limit juga berlaku untuk fungsi trigonometri. Untuk mengerjakan soal limit trigonometri dengan mantap, perlu diketahui hubungan-hubungan antar fungsi trigonometri.
Konsep limit juga berlaku untuk fungsi yang berupa fungsi trigonometri. Penyelesaiannya sama dengan limit fungsi aljabar. Penyelesaian limit fungsi trigonometri bisa dilakukan dengan melakukan perubahan-perubahan bentuk sinus, cosinus, dan tangen.
Oleh karena itu, untuk mengerjakan soal limit trigonometri dengan mantap, sangat disarankan untuk memahami terlebih dahulu hubungan-hubungan antar fungsi trigonometri atau biasa dikenal dengan identitas trigonometri. Untuk mengetahui hubungan antar fungsi trigonometri, Anda bisa baca pada artikel ini: rumus identitas fungsi trigonometri
Terdapat tiga bentuk umum dalam limit fungsi trigonometri yang akan kita pelajari. Kita akan membahasnya berikut ini.
Bentuk \( \lim_\limits{x\to c} f(x) = f(c) \)
Pada bentuk ini, kita dapat substitusi nilai \(c\) ke dalam \(x\) pada fungsi trigonometri. Sebagai contoh, perhatikan pengerjaan limit fungsi trigonometri berikut.
Contoh 1:
Tentukan limit dari \( \lim_\limits{x\to \pi/4} \sin 2x \) dan \( \lim_\limits{x\to \pi} \cos \frac{1}{2} x \).
Pembahasan:
Kita substitusi langsung nilai \(x\) ke fungsi yang ada pada limit.

Bentuk \( \lim_\limits{x\to c} \frac{f(x)}{g(x)} \)
Bentuk ini merupakan limit dengan perbandingan dua fungsi trigonometri. Kita dapat gunakan metode substitusi langsung untuk bentuk limit trigonometri ini jika hasil yang diperoleh bukan bentuk tak tentu (0/0, \( ∞/∞ \), \( ∞-∞ \), dan bentuk tak tentu lainnya). Namun, jika hasilnya dalam bentuk tak tentu, kita bisa lakukan pemfaktoran terlebih dahulu. Perhatikan contoh berikut.
Contoh 2:
Tentukan limit dari \( \lim_\limits{x\to 0} \frac{\sin 2x}{\sin x} \).
Pembahasan:
Jika melakukan substitusi langsung, kita akan memperoleh bentuk tak tentu 0/0. Karena itu, kita sederhanakan dulu fungsinya dengan pemfaktoran, kemudian baru disubstitusi nilainya.
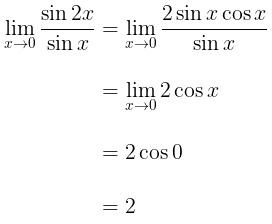
Contoh 3:
Hitunglah limit dari \( \lim_\limits{x\to 0} \frac{\sin x}{\tan \frac{1}{2} x} \).
Pembahasan:
Jika melakukan substitusi langsung, kita akan memperoleh bentuk tak tentu 0/0. Karena itu, kita sederhanakan dulu fungsinya dengan pemfaktoran, kemudian baru disubstitusi nilainya.

Baca juga:
Bentuk \( \lim_\limits{x\to 0} \frac{f(x)}{g(x)} \)
Pada bentuk ini, fungsi pada limit merupakan perbandingan antara fungsi trigonometri dengan fungsi aljabar. Beberapa rumus penting untuk bentuk ini diberikan berikut ini.

Berdasarkan rumus di atas, dapat kita kembangkan rumus-rumus berikut:

Contoh 4:
Hitunglah nilai dari \( \lim_\limits{x\to 0} \frac{\tan 3x}{3x^2+x} \).
Pembahasan:
Jika melakukan substitusi langsung, kita akan memperoleh bentuk tak tentu 0/0. Karena itu, kita sederhanakan menggunakan rumus perbandingan antara fungsi trigonometri dengan fungsi aljabar seperti diberikan di atas, kemudian baru disubstitusi nilainya.

Contoh 5:
Tentukanlah nilai dari \( \lim_\limits{x\to 0} \frac{x^2+\sin x \tan x}{1-\cos 2x} \).
Pembahasan:
Jika melakukan substitusi langsung, kita akan memperoleh bentuk tak tentu 0/0. Karena itu, kita sederhanakan menggunakan rumus perbandingan antara fungsi trigonometri dengan fungsi aljabar seperti diberikan di atas.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Nobody ever got ready by waiting. You only get ready by starting.
