www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Turunan Fungsi › Turunan Fungsi, Contoh Soal dan Pembahasan
Turunan Fungsi, Contoh Soal dan Pembahasan
Banyak fenomena dalam dunia nyata yang melibatkan perubahan kuantitas seperti kecepatan roket, inflasi mata uang, dan sebagainya. Fenomena-fenomena tersebut sering kali dapat dijelaskan dengan menggunakan konsep turunan.
Banyak fenomena dalam dunia nyata yang melibatkan perubahan kuantitas seperti kecepatan roket, inflasi mata uang, jumlah bakteri dalam suatu kultur, intensitas goncangan gempa bumi, tegangan sinyal listrik, dan sebagainya.
Fenomena-fenomena tersebut sering kali dapat dijelaskan dengan menggunakan konsep turunan atau derivatif, yakni alat matematika untuk mempelajari tingkat perubahan satu kuantitas relatif terhadap yang lain.
Kita akan mulai penjelasan dengan memberikan definisi dari turunan terlebih dahulu. Apabila fungsi \(f(x)\) mempunyai turunan untuk setiap \(x\) anggota domain \(D\), dengan \(D∈R\) (bilangan real) maka diperoleh turunan fungsi dari \(f(x)\) yang dirumuskan:

Perhatikan bahwa \( f'(x) \) menyatakan turunan dari fungsi \(f(x)\). Untuk lebih jelasnya, kita nyatakan dalam definisi berikut:
DEFINISI:
Turunan fungsi \(f\) adalah fungsi lain \(f'\) (dibaca “\(f\) aksen”) yang nilainya pada sebarang bilangan \(x\) adalah

asalkan limit ini ada.
Jika limit pada definisi di atas memang ada, maka dikatakan bahwa \(f\) terdiferensialkan (terturunkan) di \(x\). Pencarian turunan disebut pendiferensialan.
Selain notasi \( f'(x) \) seperti pada definisi di atas, terdapat cara lain yang juga bisa digunakan untuk menyatakan turunan yakni,
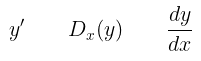
Kita akan sering menggunakan beberapa notasi tersebut secara bergantian supaya Anda dapat terbiasa ketika membaca referensi atau buku lain yang membahas tentang turunan.
Perhatikan contoh soal berikut:
Contoh 1:
Tentukanlah turunan dari \(f(x)=x^2\) dengan menggunakan definisi turunan fungsi!
Pembahasan:
Gunakan definisi turunan yang diberikan pada penjelasan di atas. Kita peroleh

Jadi, turunan dari \(f(x)=x^2\) adalah \(f'(x)=2x\).
CONTOH 2:
Jika \(f(x) = x^3 + 7x\). Cari \(f'(x)\).
Penyelesaian:

Rumus-rumus Turunan Fungsi
Proses pencarian turunan suatu fungsi langsung menggunakan definisi turunan seperti yang diberikan pada penjelasan di atas tidak hanya memakan waktu tetapi juga membosankan. Oleh karena itu, kita tidak akan terlalu sering menggunakan definisi turunan dalam mencari turunan suatu fungsi. Di sini kita akan membahas rumus-rumus terkait turunan yang sering digunakan untuk mencari turunan suatu fungsi.
Aturan Fungsi Konstanta
Jika \(f(x) = k\) dengan \(k\) suatu konstanta (misalnya 5, 10, 12 atau sembarang angka lainnya), maka untuk sebarang \(x\), \(f'(x) = 0\).
Aturan Fungsi Identitas
Jika \(f(x) = x\), maka \(f'(x) = 1\).
Kita tidak perlu memberikan contoh untuk dua aturan di atas, karena sudah sangat jelas.
Aturan pangkat
Jika \(f(x) = x^n\) dengan \(n\) bilangan-bilangan bulat positif maka \(f'(x) = nx^{n-1}\).
Contoh 3:
Diketahui fungsi \(f(x)=x^2\), carilah turunan dari fungsi tersebut.
Pembahasan:
Dari aturan pangkat, kita peroleh

Perhatikan bahwa hasil yang kita peroleh sama dengan hasil pada Contoh 1 yang menggunakan definisi turunan.
Aturan kelipatan konstanta
Jika \(k\) suatu konstanta dan \(f\) suatu fungsi yang terdiferensialkan, maka \((kf)'(x) = kf'(x)\).
Contoh 4:
Carilah turunan dari \( f(x) = 10x^2 \).
Pembahasan:
Dari aturan pangkat kita tahu bahwa turunan dari \(f(x)=x^2\) adalah \(f'(x)=2x\). Dengan demikian, dari aturan kelipatan konstanta, turunan dari \( f(x)=10x^2 \) adalah
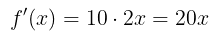
Aturan jumlah
Jika \(f\) dan \(g\) fungsi-fungsi yang terdiferensialkan, maka \((f + g)'(x) = f'(x) + g'(x)\).
Aturan Selisih
Jika \(f\) dan \(g\) fungsi-fungsi yang terdiferensialkan, maka \((f - g)'(x) = f'(x) - g'(x)\).
CONTOH 5:
Cari turunan dari \(5x^2 + 7x - 6\) dan \(4x^6 - 3x^5 - 10x^2 + 5x + 16\).
Penyelesaian:
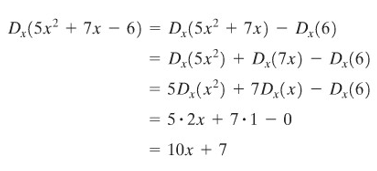
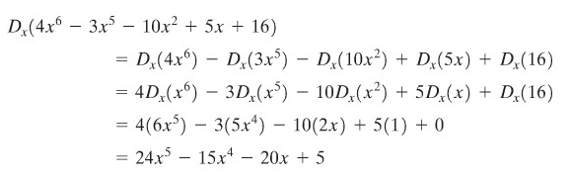
Aturan Hasil Kali
Andaikan \(f\) dan \(g\) fungsi-fungsi yang dapat didiferensialkan, maka
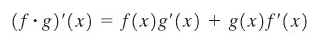
CONTOH 6:
Gunakan aturan hasil kali untuk mencari turunan \((3x^2- 5)(2x^4- x)\). Periksa jawaban dengan mengerjakan soal itu secara lain.
Penyelesaian:

Untuk memeriksa, pertama kita kalikan dan kemudian ambil turunan.
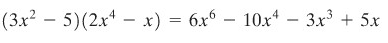
Jadi, kita peroleh hasil berikut:
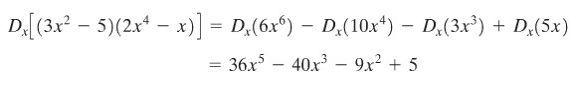
Perhatikan bahwa kedua cara menghasilkan jawaban yang sama.
Aturan Hasil Bagi
Andaikan \(f\) dan \(g\) fungsi-fungsi yang dapat didiferensialkan dengan \(g(x) ≠ 0\). Maka

CONTOH 7:
Cari turunan dari \((3x - 5)/(x^2 + 7)\).
Penyelesaian:

CONTOH 8:
Carilah turunan dari

Penyelesaian:
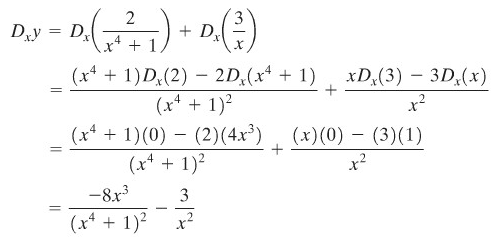
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
The person who dance with you in the rain will most likely walk with you in the storm.
