Contoh 1:

Hitung limit berikut jika ada: \( \displaystyle{ \lim_{x\to +\infty} \sqrt[3]{\frac{3x+5}{6x-8}} } \)

Pembahasan:

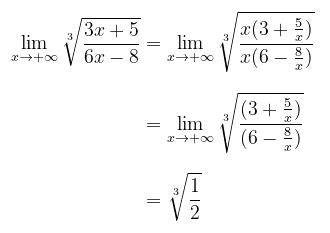
Contoh 2:

Tentukan \(a\) yang memenuhi persamaan berikut:

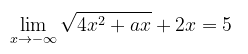
Pembahasan:

Contoh 3:

Periksalah apakah fungsi

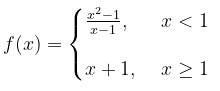
kontinu di \(x = 1\).

Pembahasan:

Jangan terkecoh dengan kerumitan dari penampakan fungsi \(f\). Perhatikan bahwa untuk \(x < 1\) berlaku

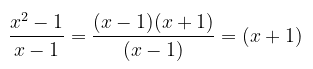
“Pencoretan” \(x-1\) pada langkah di atas adalah benar karena \(x≠1\). Dengan demikian, sebenarnya kita telah menunjukkan bahwa \(f(x)=x+1\) untuk setiap \(x\), dan telah kita ketahui bersama bahwa fungsi ini kontinu pada \(R\), khususnya pada \(x = 1\).

Contoh 4:

Tentukan nilai \(k\) supaya

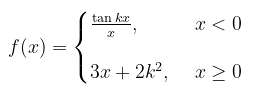
kontinu di \( x = 0\)

Pembahasan:

Agar \(f(x)\) kontinu di \(x = 0\), maka harus berlaku

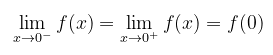
Kekontinuan kiri \(f(x)\) di \(x = 0\) dijabarkan sebagai berikut:

Jadi, agar \(f(x)\) kontinu di \(x = 0\), maka haruslah \(k∈{0, \frac{1}{2}}\).

Contoh 5:

Periksalah apakah fungsi berikut kontinu di \(x = 1\).

Pembahasan:

Untuk mengetahuinya harus diperiksa \(\displaystyle{ \lim_{x\to 1} f(x) = f(1) } \).

Sekarang perhatikan bahwa untuk sembarang nilai \(x\) kecuali \(x = 1\) berlaku

Selanjutnya, \(\displaystyle{ \lim_{x\to 1} -(x-1)^2=0 } \) dan \(\displaystyle{ \lim_{x\to 1} (x-1)^2=0 } \) , sehingga menurut teorema apit \(\displaystyle{ \lim_{x\to 1} f(x)=0 } \). Jadi, karena \(\displaystyle{ \lim_{x\to 1} f(x)=0≠f(1) } \)maka \(f\) tidak kontinu di \(x = 1\).

Contoh 6:

Diberikan fungsi sebagai berikut:

a. Tentukan hubungan antara \(p\) dan \(q\) agar fungsi \(f(x)\) kontinu di \(x=1\)

b. Tentukan nilai \(p\) dan \(q\) agar \(f'(1)\) ada!

Pembahasan:

1. Menurut hipotesisnya, kekontinuan kiri \(f(x)\) pada \(x = 1\) akan menghasilkan


Sedangkan kekontinuan kanan \(f(x)\) di \(x = 1\) menghasilkan hubungan trivial \((p+q = p + q)\). Jadi hubungan antara \(p\) dan \(q\) agar \(f(x)\) kontinu di \(x = 1\) adalah \(1 = p + q\).

2. Agar \(f’(1)\) ada, maka \(f_-' (1)=f_+' (1)\), yaitu


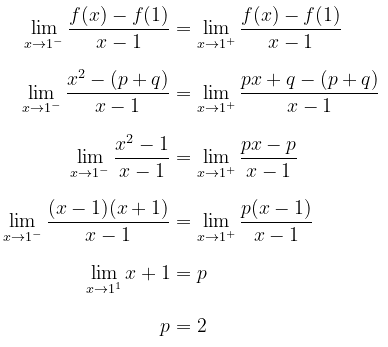
Dengan demikian, kita peroleh \(q = -1\).

Jadi, nilai \(p\) dan \(q\) adalah 2 dan \(-1\).

Contoh 7:

Diberikan fungsi sebagai berikut:

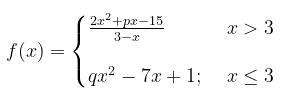
Tentukan konstanta \(p\) dan \(q\) supaya \(f(x)\) kontinu di \(x = 3\).

Pembahasan:

Agar \(f(x)\) kontinu di \(x = 3\), maka haruslah

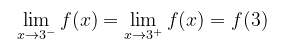
Kekontinuan kiri \(f(x)\) pada \(x = 3\) menghasilkan hubungan trivial \((9q-20=9q-20)\). Sedangkan kekontinuan kanan \(f(x)\) pada \(x = 3\) dijabarkan sebagai berikut:

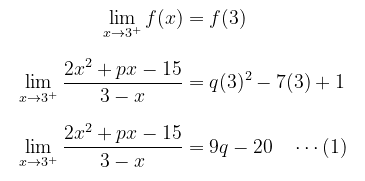
Perhatikan bahwa \(\displaystyle{ \lim_{x\to 3^+} 2x^2+px-15 } \) haruslah bernilai 0, sebab jika tidak (katakanlah \(\displaystyle{ \lim_{x\to 3^+} 2x^2+px-15 =c≠0 } \)) akan berakibat

yang menyebabkan \(f(x)\) gagal kontinu di \(x = 3\).

Sekarang, kita peroleh

Dengan mensubstitusikan hasil ini pada persamaan (i) akan memberikan

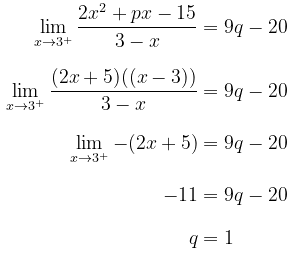
Jadi, agar \(f(x)\) kontinu di \(x = 3\), maka haruslah \(p = -1\) dan \(q = 1\).