www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Bentuk Tak Tentu › Limit Bentuk Tak Tentu ∞-∞
Limit Bentuk Tak Tentu ∞-∞
Untuk mencari limit bentuk taktentu ∞-∞, kita sering kali perlu mengubah bentuk tak tentu ini sehingga memungkinkan kita untuk menghitung limitnya.
Bentuk tak tentu lain yang akan dibahas di sini adalah ∞ - ∞. Perhatikanlah bentuk limit berikut ini:

Limit tersebut memiliki bentuk taktentu \(∞-∞\). Untuk mencari limit ini, kita sering kali perlu mengubah bentuk tak tentu ini sehingga memungkinkan kita untuk menghitung limitnya. Misalnya, contoh di atas dapat diselesaikan sebagai berikut.

Dalam beberapa kasus, kita akan menjumpai bentuk tak tentu yang muncul dalam bentuk akar. Sebagai contoh, perhatikan bentuk tak tentu ∞ - ∞ berikut ini.

Untuk menyelesaikan limit ini, kita bisa melakukan perkalian sekawan, yakni
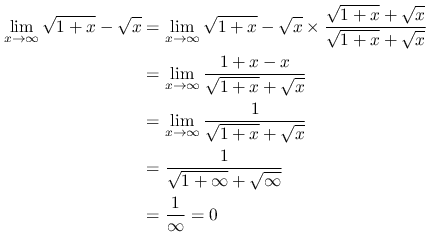
Sebuah pertanyaan yang sering muncul adalah apakah Aturan I'Hopital dapat digunakan seperti halnya pada bentuk tak tentu 0/0 dan \(∞/∞\)? Jawabannya adalah iya, tetapi hanya setelah kita menuliskan kembali persoalan tersebut dalam bentuk yang memungkinkan aturan ini berlaku. Pada kasus ini, kedua pecahan haruslah dikombinasikan, prosedur yang akan mengubah persoalan tersebut menjadi dalam bentuk 0/0 atau \(∞/∞\).
Contoh 1:
Hitunglah limit berikut jika ada.
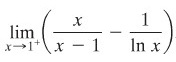
Pembahasan:
Perhatikan bahwa ini merupakan bentuk tak tentu ∞ - ∞. Hal pertama yang perlu dilakukan adalah mengubah bentuk tak tentu tersebut menjadi bentuk 0/0 atau ∞/∞. Setelah itu, penerapan Aturan I’Hopital dua kali akan menghasilkan berikut ini.

Contoh 2:
Hitunglah
Pembahasan:
Dengan substitusi nilai x maka akan diperoleh bentuk tak tentu ∞ - ∞. Untuk menerapkan Aturan I'Hopital, kita perlu mengubah bentuk tersebut menjadi bentuk 0/0 atau ∞/∞. Pertama, kita akan coba mengubahnya ke bentuk 0/0, yakni
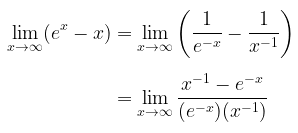
Perhatikan bahwa kita telah mengubah bentuknya menjadi 0/0 sehingga dengan menerapkan Aturan I'Hopital, kita peroleh

Kita tidak bisa menerapkan Aturan I'Hopital lagi pada hasil di atas, karena pembilang akan berupa ∞ - ∞. Malahan jika kita tuliskan kembali hasil di atas, maka kita akan peroleh bentuk yang berulang-ulang dan semakin rumit. Jika kondisi yang demikian terjadi, berhentilah dan coba cara lain yakni dengan mengubah bentuk tak tentu tersebut ke bentuk ∞/∞.
Sekarang, misalkan bahwa \(y = e^x - x\) sehingga

Jika x sama dengan ∞, maka kita peroleh bentuk ∞/∞.

Karenanya bentuknya ∞/∞, maka kita bisa terapkan Aturan I'Hopital yakni
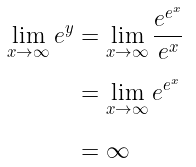
Karena \( e^y = \infty \), maka

Dengan demikian,
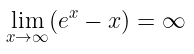
Sumber:
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Many people say that the intelligence that make the great scientists. They are mistaken…it is the character.

