www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Teknik Pengintegralan › Teknik Integral Parsial, Contoh Soal dan Pembahasan
Teknik Integral Parsial, Contoh Soal dan Pembahasan
Teknik pengintegralan yang akan kita bahas di sini dikenal dengan teknik pengintegralan parsial. Teknik ini didasarkan pada pengintegralan rumus turunan hasil kali dua fungsi.
Apabila pengintegralan dengan teknik atau metode substitusi tidak berhasil, maka teknik pengintegralan lain mungkin dapat memberikan hasil. Teknik pengintegralan yang akan kita bahas di sini dikenal dengan teknik pengintegralan parsial. Teknik ini didasarkan pada pengintegralan rumus turunan hasil kali dua fungsi.
Andaikan \(u = u(x)\) dan \(v = v(x)\). Maka
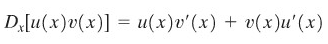
atau
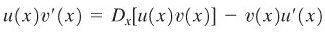
Dengan mengintegralkan dua ruas persamaan tersebut, kita peroleh

Persamaan terakhir ini dapat kita tuliskan untuk integral tentu dan tak tentu.
Pengintegralan Parsial: Integral Tak Tentu dan Integral Tentu
Karena \(dv=v'(x) \ dx\) dan \(du=u'(x) \ dx\), maka untuk integral tak tentu, pengintegralan parsial dapat dituliskan sebagai

Sedangkan rumus pengintegralan parsial untuk integral tentu adalah

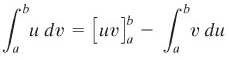
Rumus di atas memungkinkan kita memindahkan masalah pengintegralan \(u \ dv\) pada pengintegralan \(v \ du\). Pengintegralan terakhir ini tergantung pada pemilihan \(u\) dan \(dv\) yang tepat.
Gambar 1 di bawah mengilustrasikan interpretasi geometrik untuk pengintegralan parsial.

Gambar 1.
CONTOH 1:
Carilah \( \int x \cos x \ dx \).
Penyelesaian:
Kita ingin menulis \(x \cos{x} \ dx\) sebagai \(u \ dv\). Salah satu cara ialah memisalkan \(u = x\) dan \(dv = \cos{x} \ dx\). Jadi \(du = dx\) dan \(v = ∫ \cos{x} \ dx = \sin{x}\) (kita dapat menghilangkan konstanta pengintegralan). Jadi kalau kita ringkaskan subsitusi ganda tersebut, kita peroleh

Rumus pengintegralan parsial menjadi

Pengandaian \(u\) dan \(dv\) di atas tampak berhasil. Keberhasilan teknik integral sangat bergantung pada pengandaian yang digunakan. Substitusi lain, misalnya sebagai berikut.
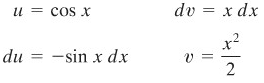
Rumus pengintegralan parsial menghasilkan
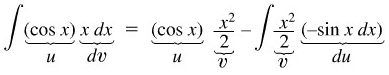
Pengandaian tersebut memang betul, akan tetapi dengan ini, integral pada ruas kanan menjadi lebih rumit. Oleh karena itu, penting sekali memilih \(u\) dan \(dv\) setepat mungkin. Yang pokok ialah bahwa integral kedua (yang berada di ruas kanan) harus diusahakan menjadi lebih sederhana.
CONTOH 2:
Carilah \( \int_1^2 \ln{x} \ dx \).
Penyelesaian:
Kita gunakan substitusi ganda sebagai berikut

Sehingga,

CONTOH 3:
Carilah \( \int \arcsin x \ dx \).
Penyelesaian:
Kita gunakan substitusi ganda sebagai berikut
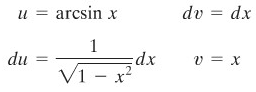
Sehingga,

CONTOH 4:
Carilah \( \int_1^2 t^6 \ln t \ dt \).
Penyelesaian:
Kita gunakan substitusi ganda sebagai berikut

Sehingga,
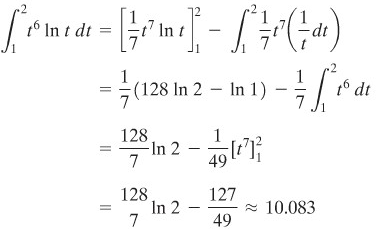
Pengintegralan Parsial Berulang
Kerap kali kita perlu gunakan pengintegralan parsial beberapa kali. Perhatikan contoh berikut.
CONTOH 5:
Carilah \( \int x^2 \sin x \ dx \).
Penyelesaian:
Andaikan

Maka,
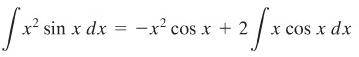
Dengan demikian tampak bahwa pangkat pada \(x\) dalam integral kedua berkurang. Ini berarti bahwa kita dapat menggunakan integral parsial lagi. Integral kedua ini telah kita hitung dalam Contoh 1. Dengan hasil yang kita peroleh di situ kita dapat menyelesaikan integral kita sebagai berikut.

CONTOH 6:
Carilah \( \int e^x \sin x \ dx \).
Penyelesaian:
Andaikan \(u = e^x\) dan \(dv = \sin{x} \ dx\). Kemudian \(du = e^x \ dx \) dan \(v = -\cos{x}\). Jadi,
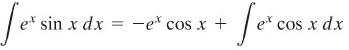
tampaknya tidak ada perbaikan. Akan tetapi dengan sekali lagi pengintegralan parsial pada integral kedua, yaitu andaikan \(u=e^x\), dan \(dv = \cos{x} \ dx\), maka \(du = e^u \ dx\) dan \(v = \sin{x}\). Sehingga

Apabila hasil ini disubstitusikan ke dalam hasil pertama, kita peroleh

Dengan mengubah urutan suku akhir ke sebelah kiri dan mengumpulkan suku-sukunya, kita peroleh,
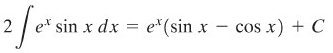
Sehingga akhirnya,
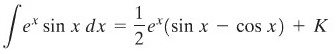
Rumus Reduksi
Suatu rumus yang berbentuk
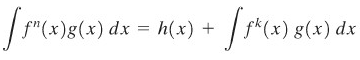
dengan \(k < n\) dinamakan rumus reduksi oleh karena pangkat dari \(f\) berkurang. Rumus demikian kerap kali diperoleh dengan menggunakan pengintegralan parsial.
CONTOH 7:
Jabarkanlah suatu rumus reduksi untuk \(∫ \sin^nx \ dx\).
Penyelesaian:
Andaikan \(u=\sin^{n-1} x\) dan \(dv = \sin{x}\ dx\), maka \(du = (n-1) \sin^{n-2}{x} \cos{x} \ dx\) dan \(v = -\cos{x}\). Sehingga,
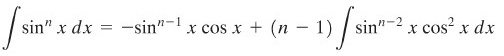
Oleh karena \(\cos^2{x}=1-\sin^2{x}\), maka apabila \(\cos^2x\) dalam integral di ruas kanan diganti dengan \(1-\sin^2{x}\), kita akhirnya memperoleh
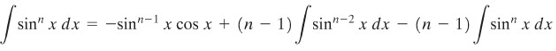
Dengan mengumpulkan integral pertama dengan integral yang terakhir, kita peroleh suatu rumus reduksi untuk \(∫ \sin^nx \ dx\) yang berlaku untuk \(n ≥ 2\).

CONTOH 8:
Gunakan rumus reduksi di atas untuk menghitung

Penyelesaian:
Perhatikan terlebih dahulu bahwa

Sehingga,

Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Orang yang lemah tidak mampu memaafkan. Memaafkan adalah ciri orang yang kuat.
