www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Bentuk Tak Tentu › Limit Bentuk Tak Tentu ∞/∞
Limit Bentuk Tak Tentu ∞/∞
Dalam banyak kasus, kita mungkin akan berjumpa dengan persoalan limit hasil bagi di mana pembilang dan penyebut menuju tak terhingga. Bentuk tersebut dinamakan limit bentuk tak tentu dari jenis ∞/∞.
Dalam banyak kasus, kita mungkin akan berjumpa dengan persoalan limit sebagai berikut.
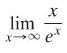
Bentuk limit ini tergolong bentuk
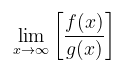
yang memiliki sifat bahwa pembilang dan penyebut menuju tak terhingga. Bentuk tersebut dinamakan bentuk tak tentu dari jenis ∞/∞. Ternyata Aturan I’Hopital juga berlaku dalam hal ini. Jadi,

TEOREMA:
Andaikan 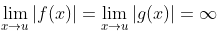

ada, baik ia terhingga atau tak-terhingga (misalnya, bilangan terhingga L, ∞, atau -∞), maka

Di sini \(u\) dapat mewakili sebarang simbol \(a,a^-,a^+,-∞\) atau \(+∞\).
CONTOH 1:

Penyelesaian:
Tampak bahwa \(x\) dan \(e^x\) menuju \(∞\) apabila \(x→∞\). Dengan menggunakan Aturan I’Hopital kita peroleh

CONTOH 2:
Apabila \(a\) bilangan riil yang positif buktikan bahwa

Penyelesaian:
Andaikan \(a = 2,5\). Maka diperlukan tiga kali penggunaan Aturan I’Hopital, yaitu

Cara yang serupa dapat digunakan untuk menghitung \(a > 0\). Misalkan \(m\) menunjukkan bilangan bulat terbesar kurang dari \(a\). Maka dengan menggunakan Aturan I’Hopital memberikan
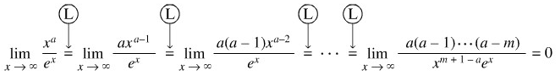
CONTOH 3:
Apabila \(a\) bilangan riil positif, buktikan bahwa

Penyelesaian:
Jelas \(\ln{x}\) dan \(x^a\) menuju tak terhingga apabila \(x→∞\). Sehingga dengan Aturan I’Hopital kita peroleh,

CONTOH 4:

Penyelesaian:
Apabila \(x→0^+\), maka \(\ln{x}→-∞\) dan \(\cot{x}→∞\), dengan demikian kita dapat menggunakan Aturan I’Hopital, sehingga

Limit terakhir ini masih tetap bentuknya, yakni berupa ∞/∞. Walaupun demikian kita tidak akan menggunakan Aturan I’Hopital lagi, sebab bentuk tersebut akan menjadi makin rumit. Untuk menghitung limit terakhir itu, kita perlu ubah menjadi.

Sehingga

Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Try not to be a man of success, rather a man of value.
