www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Limit dan Kekontinuan › Konsep dan Definisi Limit
Konsep dan Definisi Limit
Definisi dari limit menyatakan bahwa suatu fungsi f(x) akan mendekati suatu nilai tertentu jika x mendekati nilai tertentu.
Pandang fungsi yang ditentukan oleh rumus
\[ f(x) = \frac{x^3-1}{x-1} \]
Perhatikan bahwa fungsi tersebut tidak terdefinisikan pada \(x =1\) karena di titik ini \(f(x)\) berbentuk \(0/0\), yang mana tidak mempunyai arti.
Akan tetapi, kita masih dapat menanyakan apa yang terjadi pada \(f(x)\) bilamana \(x\) mendekati 1 atau lebih tepatnya, apakah \(f(x)\) mendekati bilangan tertentu bilamana \(x\) mendekati 1? Untuk sampai pada pertanyaan ini, kita telah melakukan tiga hal.
Pertama, kita telah menghitung beberapa nilai \(f(x)\) untuk \(x\) dekat 1. Kedua, kita menunjukkan nilai-nilai ini dalam sebuah diagram skematis (schematic diagram), dan terakhir kita telah mensketsakan grafik \(y = f(x)\) (Gambar 1).

Gambar 1
Semua informasi yang telah kita sajikan di atas kelihatannya menunjuk ke kesimpulan yang sama yakni \(f(x)\) mendekati 3 jika \(x\) mendekati 1. Dalam lambang matematis, kita tuliskan
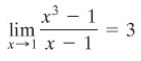
Ini dibaca “limit dari \((x^2 - 1)/(x - 1)\) untuk \(x\) mendekati 1 adalah 3.”
Tentu saja kita bisa menyelesaikan contoh di atas dengan memanfaatkan sedikit aljabar yakni dengan menguraikan selisih pangkat tiga, sehingga diperoleh

Perhatikan bahwa \((x - 1)/(x - 1) = 1\) selama \(x ≠ 1\) sehingga kita bisa mencoretnya pada pembilang dan penyebut.
Agar yakin bahwa kita berada pada jalur yang benar, kita perlu mempunyai pengertian yang jelas tentang arti perkataan limit. Kita definisikan limit sebagai berikut.
Definisi Limit
Untuk mengatakan bahwa \(\displaystyle{\lim_{x \to c}}\,f(x)=L\) berarti bahwa bilamana \(x\) dekat tetapi berlainan dari \(c\), maka \(f(x)\) dekat ke \(L\).
Contoh 1: Mencari Limit
Carilah \( \displaystyle{\lim_{x \to 3}\, (4x-5) } \).
Penyelesaian:
Bilamana \(x\) dekat 3; maka \((4x - 5)\) dekat terhadap \((4 \cdot 3 - 5) = 7\). Kita tuliskan

Contoh 2: Mencari Limit
Carilah \( \displaystyle{\lim_{x \to 3}\, \frac{x^2-x-6}{x-3} } \).
Penyelesaian:
Perhatikan bahwa \((x^2 - x - 6)/(x - 3)\) tidak terdefinisi di \(x = 3\), tetapi itu tidak apa. Untuk mendapatkan gagasan tentang apa yang terjadi bilamana \(x\) mendekati 3, kita dapat memakai sedikit aljabar untuk menyederhanakan persoalan. Kita peroleh hasil berikut.

Ternyata keadaannya tidak semudah apa yang kelihatan. Perhatikan kembali Contoh 2 di atas. Untuk memperoleh gagasan tentang apa yang terjadi bilamana \(x\) mendekati 3, kita dapat mengambil sembarang nilai \(x\) yang mendekati 3, dan kemudian menggunakan kalkulator untuk menghitung nilai \(f(x)\).
Namun, kalkulator tidak selalu dapat membantu, malahan mungkin mengecohkan kita. Perhatikan contoh berikut.
Contoh 3:
Carilah \( \displaystyle{\lim_{x \to 0}\, \left[ x^2 - \frac{\cos{x}}{10,000} \right] } \).
Penyelesaian:
Dengan mengikut prosedur yang digunakan sebelumnya, kita susun tabel nilai yang diperlihatkan dalam Gambar 2. Kesimpulan yang disarankannya adalah bahwa limit yang diinginkan adalah 0. Tetapi itu salah. Jika kita ingat kembali grafik \(y = \cos{x}\), kita sadari bahwa \(\cos{x}\) mendekati 1 untuk \(x\) mendekati 0. Jadi,


Gambar 2
Limit Kiri dan Limit Kanan
DEFINISI: Limit kiri dan limit kanan
Untuk mengatakan bahwa \(\displaystyle{\lim_{x \to c^+}}\, f(x) = L\) berarti bahwa bilamana \(x\) dekat tetapi pada sebelah kanan \(c\), maka \(f(x)\) adalah dekat ke \(L\). Serupa, untuk mengatakan bahwa \(\displaystyle{\lim_{x \to c^-}}\, f(x) = L\) berarti bahwa bilamana \(x\) dekat tetapi pada sebelah kiri \(c\), maka \(f(x)\) dekat ke \(L\).
DEFINISI: Limit kiri dan limit kanan
\(\displaystyle{\lim_{x \to c}}\, f(x) = L\) jika dan hanya jika limit kiri \(\displaystyle{\lim_{x \to c^-}}\, f(x) \) dan limit kanan \(\displaystyle{\lim_{x \to c^+}}\, f(x) \) sama dengan \(L\). Jadi,
\[ \lim_{x \to c}\, f(x) = \lim_{x \to c^-}\, f(x) = \lim_{x \to c^+}\, f(x) = L \]
Cukup sekian penjelasan mengenai konsep dan definisi limit beserta contoh soal dan pembahasannya dalam artikel ini. Semoga bermanfaat.
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
You can’t put a limit on anything. The more you dream, the farther you get.
