Kalkulus I   »   Fungsi   ›  Fungsi Invers

Fungsi Invers

Fungsi yang membatalkan, atau membalikkan, efek dari fungsi \(ƒ\) disebut kebalikan dari \(ƒ\) atau invers dari \(ƒ\). Banyak fungsi umum, meskipun tidak semua, dipasangkan dengan sebuah invers.

Fungsi yang membatalkan, atau membalikkan, efek dari fungsi \(ƒ\) disebut kebalikan dari \(ƒ\) atau invers dari \(ƒ\). Banyak fungsi umum, meskipun tidak semua, dipasangkan dengan sebuah invers.

Karena tidak semua fungsi mempunyai invers atau kebalikan dari fungsi tersebut, maka pertanyaan yang kemudian muncul adalah kapan suatu fungsi mempunyai invers? Untuk menjawab ini kita perlu mengenal apa yang dikenal dengan fungsi satu-satu.

Fungsi Satu-Satu

Fungsi adalah aturan yang menetapkan nilai dari daerah hasilnya (range) ke setiap elemen dalam daerah asalnya (domain). Beberapa fungsi menetapkan nilai range yang sama untuk lebih dari satu elemen dalam domain. Fungsi \(f(x)=x^2\) menetapkan nilai yang sama, 1, untuk kedua angka -1 dan +1; sinus \(π/3\) dan \(2π/3\) keduanya bernilai \(\sqrt{3}/2\).

Fungsi lainnya mengasumsikan setiap nilai dalam range-nya tidak lebih dari sekali. Akar kuadrat dan kubik dari angka yang berbeda selalu berbeda. Fungsi yang memiliki nilai berbeda pada elemen berbeda dalam domainnya disebut fungsi satu-satu. Fungsi-fungsi ini mengambil satu nilai dalam range tepat sekali. Mari kita nyatakan dalam definisi berikut

Grafik fungsi satu-satu \(y = f(x)\) memotong garis horizontal paling banyak sekali (Gambar 1). Jika memotong garis lebih dari satu kali, ia mengasumsikan nilai-\(y\) yang sama lebih dari sekali, dan karenanya bukan fungsi satu-satu (Gambar 2). Kita nyatakan dalam teorema berikut ini.

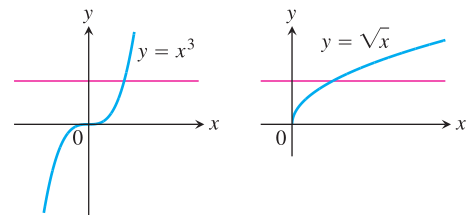
Gambar 1. Grafik \(y=x^3\) dan \(y=\sqrt{x}\) adalah fungsi satu-satu

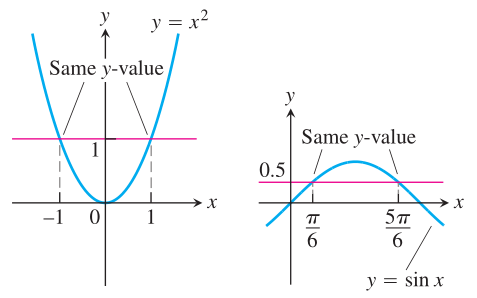
Gambar 2. Fungsi \(y=x^2\) dan \(y=\sin ⁡x\) bukan fungsi satu-satu

Dengan menggunakan uji garis horisontal, kita melihat bahwa \(y=x^3\) dan \(y=\sqrt{x}\) pada Gambar 1 adalah fungsi satu-satu pada domain \((-∞,∞)\) dan \([0,∞)\). Kedua grafik bertemu tiap garis horisontal paling banyak sekali sehingga merupakan fungsi satu-satu dan karenanya mempunyai invers.

Namun, fungsi \(y=x^2\) dan \(y=\sin ⁡x\) pada Gambar 2 adalah tidak satu-satu pada domain \((-∞,∞)\), karena kedua grafik bertemu satu atau lebih garis horisontal lebih dari sekali.

Fungsi Invers dan Grafik Fungsi Invers

Karena setiap output dari fungsi satu-satu berasal dari hanya satu input, efek dari fungsi dapat dibalik untuk mengirim output kembali ke input dari mana ia berasal.

Grafik Fungsi Invers

Tujuan kita berikutnya adalah meninjau hubungan antara grafik \(f\) dan \(f^{-1}\). Untuk tujuan ini, kita akan gunakan \(x\) sebagai variabel independen untuk kedua fungsi sehingga kita bisa membandingkan grafik \(y = f(x)\) dan \(y = f^{-1} (x)\).

Jika \((a,b)\) adalah titik pada grafik \(y = f(x)\), maka \(b = f(a)\). Ini ekuivalen dengan pernyataan bahwa \(a=f^{-1} (b)\), yang berarti bahwa \((b,a)\) adalah titik pada grafik \(y=f^{-1} (x)\). Singkatnya, dengan membalikkan koordinat sebuah titik pada grafik \(f\) menghasilkan titik pada grafik \(f^{-1}\).

Demikian pula, membalikan koordinat pada grafik \(f^{-1}\) menghasilkan titik pada grafik \(f\). Namun, efek geometrik membalikkan koordinat titik adalah mencerminkan titik itu terhadap garis \(y = x\) (Gambar 3.a) dan karena itu grafik \(y = f(x)\) dan \(y=f^{-1} (x)\) adalah percerminan satu sama lain terhadap garis \(y=x\) (Gambar 3.b). Kita nyatakan dalam teorema berikut ini.

Gambar 3. (a) Titik \((a,b)\) dan \((b,a)\) adalah percerminan terhadap \(y = x\). (b) grafik \(f\) dan \(f^{-1}\) adalah pencerminan terhadap \(y = x\).

Membatasi Domain Supaya Mempunyai Invers

Sebuah fungsi \(g\) yang diperoleh dari sebuah fungsi \(f\) dengan memberikan batasan pada domain \(f\) disebut batasan dari \(f\). Dengan demikian, fungsi \[ g(x)=x^3, \quad x≥0 \] merupakan batasan dari fungsi \(f(x)=x^3\). Lebih tepatnya, ia disebut batasan \(x^3\) untuk interval \([0,+∞]\).

Kadang-kadang adalah hal yang memungkinkan untuk memperoleh fungsi invers dari sebuah fungsi yang tidak mempunyai invers (fungsi yang tidak dapat dibalik) dengan membatasi domain secara tepat. Misalnya, kita tunjukkan sebelumnya bahwa \(f(x)=x^2\) tidak dapat dibalik. Namun, perhatikan fungsi batasan berikut

Gabungan dari kedua grafik membentuk grafik lengkap dari \(f(x)=x^2\) seperti ditunjukkan dalam Gambar 4 berikut.

Gambar 4. Grafik fungsi \( y=x^2, \ x≤0 \) dan \( y=x^2, \ x≥0 \)

Fungsi yang dibatasi ini adalah fungsi satu-satu (karena itu dapat dibalikkan atau mempunyai invers), karena grafiknya lulus uji garis horizontal. Fungsi inversnya dapat dilihat pada Gambar 5 di bawah ini.

Gambar 5. Grafik fungsi \( y=x^2, \ x≤0 \) dan \( y=x^2, \ x≥0 \) serta fungsi-fungsi invers yang bersesuaian dengannya.

Fungsi Turun dan Fungsi Naik adalah fungsi yang Dapat Dibalik

Fungsi yang grafiknya selalu naik saat dilintasi dari kiri ke kanan dikatakan sebagai fungsi yang meningkat, dan fungsi yang grafiknya selalu turun saat dilintasi dari kiri ke kanan dikatakan sebagai fungsi yang menurun. Jika \(x_1\) dan \(x_2\) adalah titik dalam domain fungsi \(f\), maka \(f\) meningkat jika

dan \(f\) turun jika

Kita dapat membuktikan secara geometri bahwa fungsi naik dan fungsi turun lulus uji garis horisontal dan karena itu dapat dibalik. Perhatikan Gambar 6 berikut yang menunjukkan fungsi naik dan fungsi turun

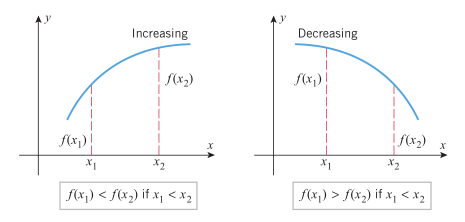
Gambar 6.

Cukup sekian penjelasan tentang fungsi invers atau kebalikan dari suatu fungsi dalam artikel ini. Semoga bermanfaat.

Sumber:

Anton, Howard., et al. (2012). Calculus, 10th ed. Hoboken: John Wiley & Sons, Inc.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.