
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Bentuk Tak Tentu › Limit Bentuk Tak Tentu 0/0
Joki Tugas Matematika Murah, Hanya Rp10-20 Ribu. Hub. WA: 0812-5632-4552
Limit Bentuk Tak Tentu 0/0
Perhatikanlah tiga masalah limit yang diberikan di bawah ini

Kalian pasti tidak asing lagi dengan bentuk limit di atas. Ketiga bentuk limit tersebut memiliki penampilan yang sama yaitu terdapat hasil bagi dan memiliki pembilang dan penyebut berlimit nol. Khusus untuk limit yang ketiga sebenarnya merupakan definisi turunan \(f'(a)\).
Kalau kita menghitung limit itu dengan mensubstitusikan nilai \(x\) pada fungsi pembilang dan penyebut, kita akan memperoleh jawaban yang tak ada artinya, yaitu 0/0. Namun demikian, kita tidak mengatakan bahwa limit tersebut tidak ada, melainkan kita hanya mengatakan bahwa limit tersebut tidak dapat ditentukan dengan aturan hasil bagi limit.
Anda tentunya masih ingat bahwa dengan menggunakan geometri, kita dapat membuktikan bahwa
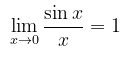
Di lain pihak, dengan menggunakan pemfaktoran dalam aljabar, kita peroleh

Kita telah berhasil menyelesaikan dua bentuk limit di atas dengan menggunakan geometri dan pemfaktoran aljabar, tetapi tentunya akan lebih baik bila ada aturan baku yang dapat dipakai untuk menghitung limit-limit demikian. Memang ada, yaitu suatu aturan yang lazim dinamakan Aturan I’Hopital (baca: loupital).
Aturan I’Hopital.
Pada tahun 1696, Guillaume Francois Antoine de I’Hopital menerbitkan buku pertama tentang kalkulus diferensial; di dalamnya ada aturan di bawah ini, yang ia peroleh dari gurunya bernama Johann Bernoulli.
TEOREMA: Aturan I'Hopital
Andaikan 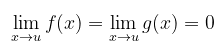
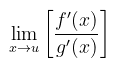
ada, baik ia terhingga atau tak-terhingga (misalnya, bilangan terhingga L, ∞,atau-∞), maka
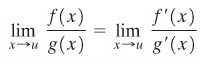
Di sini \(u\) dapat mewakili sebarang simbol \(a,a^-,a^+,-∞\) atau \(+∞\).
Mari kita lihat beberapa contoh penerapan dari aturan I’Hopital. Perhatikan bahwa dalam aturan I’Hopital, suatu limit dapat diganti dengan limit lain yang lebih sederhana dan tidak lagi berbentuk 0/0.
CONTOH 1:
Gunakan aturan I’Hopital untuk membuktikan bahwa
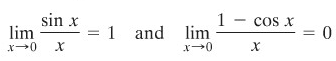
Penyelesaian:
Jika kita mensubstitusikan nilai x pada fungsi pembilang dan penyebut, kita akan peroleh dua limit tersebut berbentuk 0/0. Oleh karena itu, kita dapat menggunakan aturan I’Hopital yaitu sebagai berikut.

Jadi, limit yang pertama adalah 1 dan limit yang kedua adalah bernilai 0.
CONTOH 2:

Penyelesaian:
Kedua limit berbentuk 0/0. Oleh karena itu, kita dapat menggunakan aturan I’Hopital sebagai berikut,

Jadi, jawaban untuk limit yang pertama adalah 6/5 dan limit yang kedua adalah takhingga. Kalian juga bisa menghitung limit yang pertama dengan menggunakan pemfaktoran aljabar dan jawaban yang diberikan akan tetap sama yaitu 6/5.
CONTOH 3:

Penyelesaian:
Jika kita substitusikan nilai x pada fungsi pembilang dan penyebut, akan diperoleh bentuk 0/0. Sehingga menurut aturan I’Hopital, kita peroleh,
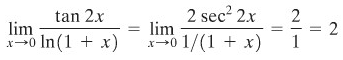
Jadi, jawaban untuk limit tersebut adalah 2.
Anda perlu ingat bahwa sering kali \(\lim f'(x)/g'(x)\) juga berbentuk 0/0. Oleh karena itu kita dapat lagi menggunakan aturan I’Hopital. Lihatlah contoh berikut ini:
CONTOH 4:

Penyelesaian:
Kita dapat menggunakan aturan I’Hopital berturut-turut tiga kali, sebagai berikut,
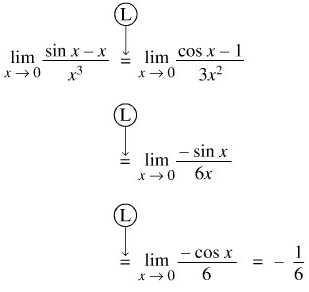
Walaupun Aturan I’Hopital mudah digunakan, tetapi kita harus hati-hati dalam pemakaiannya, khususnya harus diteliti apakah benar persyaratan yang diminta terpenuhi. Apabila tidak, kita dapat melakukan kesalahan-kesalahan seperti dalam contoh di bawah ini.
CONTOH 5:

Penyelesaian:

Penerapan pertama Aturan I’Hopital benar, penerapan kedua salah, oleh karena limit kedua tidak berbentuk 0/0. Yang benar adalah sebagai berikut,
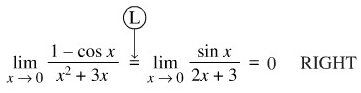
Kita berhenti mendiferensialkan, apabila ada pembilang atau penyebut berlimit tak nol.
Walaupun aturan I’Hopital dapat digunakan adakalanya aturan itu tidak dapat menolong kita; lihatlah contoh berikut ini.
CONTOH 6:

Penyelesaian:
Kita dapat menerapkan aturan I’Hopital sebanyak kita mau
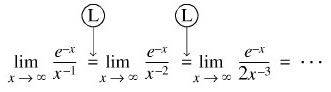
Tampak bentuk yang kita peroleh makin rumit. Jalan terbaik ialah sebagai berikut,

Dalam bentuk ini, limit kita berbentuk ∞/∞, bentuk tak tentu ini kita bahas dalam bagian berikutnya. Akan tetapi, kalian dapat menduga bahwa limit itu adalah 0, karena \(e^x\) nilainya naik lebih cepat dari \(x\) (lihat Gambar 1).

Gambar 1
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
The strong person is not the one who can wrestle someone else down. The strong person is the one who can control himself when he is angry.