www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Fungsi › Operasi pada Fungsi
Operasi pada Fungsi
Dua bilangan dapat ditambahkan untuk menghasilkan sebuah bilangan baru, demikian pula dua fungsi dapat ditambahkan untuk menghasilkan sebuah fungsi baru.
Sama halnya dengan dua bilangan a dan b yang dapat ditambahkan untuk menghasilkan sebuah bilangan baru a + b, demikian pula dua fungsi f dan g dapat ditambahkan untuk menghasilkan sebuah fungsi baru f + g. Ini baru salah satu dari beberapa operasi pada fungsi yang akan dijelaskan dalam artikel ini.
Pandanglah fungsi-fungsi f dan g dengan rumus-rumus

Dari dua fungsi tersebut, kita dapat membuat sebuah fungsi baru f + g, yakni

Tentu saja kita harus sedikit hati-hati mengenai daerah asal. Jelas x harus berupa sebuah bilangan di mana f maupun g berlaku. Dengan kata lain, daerah asal f + g adalah irisan dari daerah asal f dan g (Gambar 1).

Gambar 1
Selain fungsi f + g, kita juga peroleh fungsi-fungsi baru yakni f-g, f.g, dan f/g. Dengan anggapan bahwa f dan g mempunyai daerah asal mula, kita peroleh sebagai berikut.

Kita harus mengecualikan 0 dari daerah asal f/g untuk menghindari pembagian oleh 0.
Kita juga boleh memangkatkan suatu fungsi. Dengan \(f^n\), kita maksudkan fungsi yang memberikan nilai \([f(x)]^n\) pada x. Jadi

Contoh 1:
Andaikan \(F(x)=\sqrt[4]{x+1}\) dan \(G(x)=\sqrt{9-x^2}\), dengan masing-masing daerah asal natural [-1,∞) dan [-3,3]. Cari rumus untuk F+G, F-G, F⋅G ,F/G dan\( F^5\) dan berikan daerah asal naturalnya (domain).
Penyelesaian:

Komposisi Fungsi
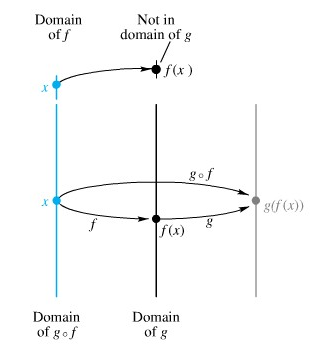
Jika f bekerja pada x untuk menghasilkan f(x) dan kemudian g bekerja pada f(x) untuk menghasilkan g(f(x)), dikatakan bahwa kita telah menyusun g dengan f. Fungsi yang dihasilkan, disebut komposisi g dengan f, dinyatakan oleh g o f. Jadi,

Ingat kembali contoh kita yang terdahulu, f(x)=(x-3)/2 dan g(x)=√x. Kita dapat menyusunnya dalam dua cara,

Segera kita perhatikan satu hal: Susunan (komposisi) fungsi tidak komutatif; g o f dan f o g umumnya berlainan.
Kita juga harus hati-hati dalam menguraikan daerah asal suatu fungsi komposit. Daerah asal g o f adalah bagian dari daerah asal f (yakni, nilai-nilai x itu) untuk mana g dapat menerima f(x) sebagai masukan. Dalam contoh kita, daerah asal g o f adalah [3,∞), karena x harus lebih besar atau sama dengan 3 agar memberikan suatu bilangan tak negatif (x-3)/2 untuk dikerjakan oleh g. Diagram dalam Gambar 3 memberikan pandangan lain mengenai hal ini.
Contoh 2:
Andaikan \(f(x)=6x/(x^2-9)\) dan \(g(x)=\sqrt{3x}\). Pertama, cari (f o g)(12); kemudian cari (f o g)(x) dan berikan daerah asalnya.
Penyelesaian:

Daerah asal f o g adalah [0,3)∪(3,∞). Perhatikan bahwa 3 dikecualikan dari daerah asal untuk menghindari pembagian oleh 0.
Mendekomposisikan fungsi komposit
Dalam kalkulus, kita akan seringkali perlu mengambil suatu fungsi yang diketahui dan mendekomposisinya – yaitu memecahnya menjadi potongan-potongan komposit. Biasanya ini dapat dilakukan dalam beberapa cara. Misalnya, ambil \(p(x)=\sqrt{x^2+4}\). Kita dapat memikirkannya sebagai

atau sebagai

Contoh 3:
Tuliskan fungsi \(p(x)=(x+2)^5\) sebagai sebuah fungsi komposit g o f
Penyelesaian:
Cara yang paling mudah untuk melakukannya adalah menuliskan

Translasi
Dengan mengamati bagaimana sebuah fungsi dibentuk dari yang lebih sederhana dapat sangat membantu dalam penggambaran grafik. Mungkin ada pertanyaan: Bagaimana grafik-grafik dari

berkaitan satu sama lain? Ambillah \(f(x)=|x|\) sebagai contoh. Keempat grafik yang bersangkutan diperagakan dalam Gambar 4.

Gambar 4
Apa yang terjadi dengan f(x)=|x| adalah khas. Perhatikan bahwa keempat grafik tersebut mempunyai bentuk sama; tiga yang terakhir hanya penggeseran (translasi) dari yang pertama. Dengan mengganti x oleh x – 3 akan menggeser grafik itu 3 satuan ke kanan; dengan menambahkan 2 berarti menggesernya ke atas sebesar 2 satuan.
Gambar 5 memberikan ilustrasi lain dari prinsip ini untuk fungsi \(f(x)=x^3+x^2\).

Gambar 5.
Prinsip yang sama secara tepat berlaku dalam situasi yang umum. Ini diilustrasikan dalam Gambar 6.

Gambar 6
Jika h < 0, maka penggeserannya ke kiri; jika k < 0, penggeserannya ke bawah.
Contoh 4:
Buatlah sketsa grafik \(g(x)=\sqrt{x+3}+1\) dengan mula-mula menggambarkan grafik \(f(x)=\sqrt{x}\) dan kemudian melakukan penggeseran-penggeseran seperlunya.
Penyelesaian:
Grafik dari g (Gambar 8) dapat anda peroleh dengan menggeser grafik dari f (Gambar 7) 3 satuan ke kiri dan 1 satuan ke atas.
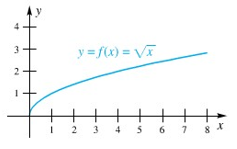
Gambar 7

Gambar 8
Cukup sekian penjelasan tentang operasi pada fungsi beserta contoh soal dan pembahasannya dalam artikel ini. Semoga bermanfaat.
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Jangan biarkan opini orang lain menenggelamkan suara dari dalam diri Anda.
