www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Aplikasi Turunan › Kemonotonan dan Kecekungan Fungsi
Kemonotonan dan Kecekungan Fungsi
Andaikan \(f\) terdiferensialkan pada selang terbuka I. Kita katakan bahwa \(f\) (serta grafiknya) adalah cekung ke atas pada I jika \(f'\) naik dan kita katakan bahwa \(f\) cekung ke bawah pada I jika \(f'\) turun pada I.
Perhatikan grafik pada Gambar 1. Tak seorang pun akan terkejut bilamana kita mengatakan bahwa \(f\) turun di kiri \(c\) dan naik di kanan \(c\). Tetapi untuk menyakinkan lagi, kita akan memberikan definisi-definisinya yang lebih persis.
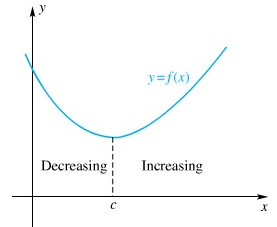
Gambar 1
DEFINISI:
Andaikan \(f\) terdefinisi pada selang \(I\) (terbuka, tertutup, atau tak satu pun). Kita katakan bahwa:
- \(f\) adalah naik pada \(I\) jika untuk setiap pasang bilangan \(x_1\) dan \(x_2\) dalam \(I\),
- \(f\) adalah turun pada \(I\) jika untuk setiap pasang bilangan \(x_1\) dan \(x_2\) dalam \(I\),
- \(f\) monoton murni (strictly monotonic) pada \(I\) jika ia naik pada \(I\) atau turun pada \(I\).

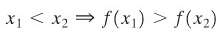
Bagaimana kita memutuskan di mana suatu fungsi naik? Seseorang mungkin menyarankan kita menggambar grafiknya dan memperhatikannya. Tetapi sebuah grafik biasanya digambar dengan merajah beberapa titik dan menghubungkan titik-titik tersebut dengan suatu kurva mulus. Siapa yang dapat yakin bahwa grafik tidak bergoyang di antara titik-titik yang dirajah. Kita memerlukan prosedur yang lebih baik.
Turunan Pertama dan Kemonotonan
Ingat kembali bahwa turunan pertama \(f'(x)\) memberi kita kemiringan dari garis singgung pada grafik \(f\) di titik \(x\). Kemudian jika \(f'(x)>0\), garis singgung naik ke kanan (lihat gambar 2). Demikian pula, jika \(f'(x)<0\), garis singgung jatuh ke kanan.

Gambar 2
TEOREMA A: Teorema Kekontinuan
Andaikan \(f\) kontinu pada selang \(I\) dan dapat didiferensialkan pada setiap titik dalam dari \(I\).
- jika \(f'(x)>0\) untuk semua titik dalam \(x\) dari \(I\), maka \(f\) naik pada \(I\)
- jika \(f'(x)<0\) untuk semua titik dalam \(x\) dari \(I\), maka \(f\) turun pada \(I\).
Teorema ini biasanya membolehkan kita secara persis menentukan di mana suatu fungsi yang terdiferensialkan naik dan di mana ia turun.
CONTOH 1:
Jika \(f(x)=2x^3-3x^2-12x+7\), cari di mana \(f\) naik dan di mana turun.
Penyelesaian:
Kita mulai dengan mencari turunan \(f\).

Kita perlu menentukan di mana \((x+1)(x-2)>0\) dan juga di mana
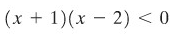
Masalah mengenai pertidaksamaan telah kita bahas sebelumnya, jadi harusnya kita tidak kesulitan untuk menyelesaikan persoalan ini. Titik-titik pemisah adalah – 1 dan 2; mereka membagi sumbu-x atas tiga selang; \((-∞,-1),(-1,2)\), dan \((2,∞)\). Dengan memakai titik-titik uji – 2, 0, dan 3, kita simpulkan bahwa \(f'(x)>0\) pada yang pertama dan terakhir dari selang-selang ini dan bahwa \(f'(x)<0\) pada selang tengah (Gambar 3).
Jadi menurut Teorema A, \(f\) naik pada \((-∞,-1]\) dan \([2,∞)\); ia turun pada \([-1,2]\). Perhatikan bahwa teorema tersebut membolehkan kita mengikutkan titik-titik ujung dari selang-selang ini, walaupun \(f'(x)=0\) pada titik-titik itu. Grafik \(f\) diperlihatkan dalam Gambar 4.

Gambar 3
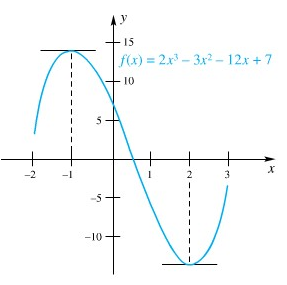
Gambar 4
CONTOH 2:
Tentukan di mana \(g(x)=x/(1+x^2)\) naik dan di mana ia turun.
Penyelesaian:

Karena penyebut selalu positif, \(g'(x)\) mempunyai tanda sama seperti \((1-x)(1+x)\). Titik-titik pemisah -1 dan 1, menunjukkan tiga selang \((-∞,-1), (-1,1)\), dan \((1,∞)\). Bilamana kita menguji mereka, kita temukan bahwa \(g'(x) < 0\) pada selang-selang yang pertama dan ketiga dan bahwa \(g'(x) > 0\) pada selang yang tengah (Gambar 5).
Kita simpulkan dari Teorema A bahwa \(g\) turun pada \((-∞,-1]\) dan \([1,∞)\), naik pada selang \([-1,1]\). Kita tunda penggambaran grafik \(g\) sampai nanti, tetapi jika anda ingin melihat grafiknya, beralihlah ke Contoh 4.

Gambar 5
Turunan kedua dan kecekungan
DEFINISI:
Andaikan \(f\) terdiferensialkan pada selang terbuka \(I\). Kita katakan bahwa \(f\) (serta grafiknya) adalah cekung ke atas pada \(I\) jika \(f'\) naik dan kita katakan bahwa \(f\) cekung ke bawah pada \(I\) jika \(f'\) turun pada \(I\).
Diagram dalam gambar 6 akan membantu memperjelas gagasan ini. Perhatikan bahwa kurva yang cekung ke atas berbentuk seperti sebuah cangkir.

Gambar 6
Sehubungan dengan Teorema A, kita mempunyai kriteria sederhana untuk memutuskan di mana kurva cekung ke atas dan di mana cekung ke bawah. Kita cukup mengingat dalam hati bahwa turunan kedua dari \(f\) adalah turunan pertama dari \(f'\). Jadi \(f'\) naik jika \(f''\) positif dan \(f'\) turun jika \(f''\) negatif.
DEFINISI: Teorema Kecekungan
Andaikan \(f\) terdiferensial dua kali pada selang terbuka (a,b).
- Jika \(f''>0\) untuk semua \(x\) dalam \((a,b)\), maka \(f\) cekung ke atas pada \((a,b)\)
- Jika \(f''<0\) untuk semua \(x\) dalam \((a,b)\), maka \(f\) cekung ke bawah pada \((a,b)\)
CONTOH 3:
Di mana fungsi \(f(x)=1/3 x^3-x^2-3x+4\) naik, turun, cekung ke atas, dan cekung ke bawah?
Penyelesaian:
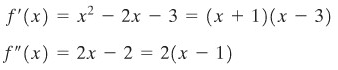

Gambar 7
Dengan menyelesaikan pertaksamaan \((x+1)(x-3)>0\) dan lawannya kita simpulkan bahwa \(f\) naik pada \((-∞,-1]\) dan \([3,∞)\) dan turun pada \([-1,3]\) (Gambar 7). Demikian pula, penyelesaian \(2(x-1)>0\) dan \(2(x-1)<0\) memperlihatkan bahwa \(f\) cekung ke atas pada \((1,∞)\), cekung ke bawah pada \((-∞,1)\). Grafik \(f\) diperlihatkan pada Gambar 8.

Gambar 8
CONTOH 4:
Di mana \(g(x)=x/(1+x^2)\) cekung ke atas dan di mana cekung ke bawah? Sketsakan grafik \(g\)?
Penyelesaian:
Kita mulai pembahasan fungsi ini dalam Contoh 2. Di sana kita mempelajari bahwa \(g\) turun pada \((-∞,-1]\) dan \([1,∞)\) dan naik pada \([-1,1]\). Untuk menganalisis kecekungan, hitung \(g''\).
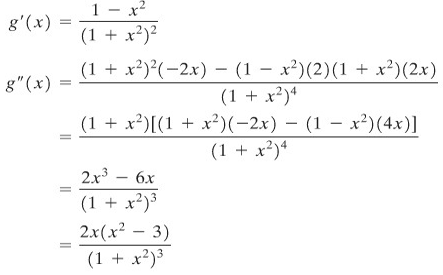

Gambar 9
Karena penyebut selalu positif, kita hanya perlu menyelesaikan \(x(x-3)>0\) dan lawannya. Titik-titik pemisah ini menentukan empat selang. Setelah menguji mereka (Gambar 9), kita simpulkan bahwa \(g\) cekung ke atas pada \((-√3,0)\) dan \((√3,∞)\) dan cekung ke bawah pada \((-∞,-√3)\) dan \((0,√3)\).
Untuk membuat sketsa grafik \(g\) kita memanfaatkan semua informasi yang sedemikian jauh telah diperoleh, ditambah dengan fakta bahwa \(g\) sebuah fungsi ganjil yang grafiknya simetri terhadap titik asal (Gambar 10).

Gambar 10
Titik Balik (Inflection Point)
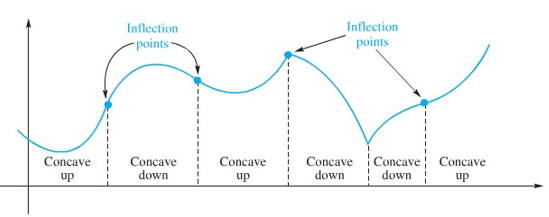
Andaikan \(f\) kontinu di \(c\). Kita sebut \((c,f(c))\) suatu titik balik dari grafik \(f\) jika \(f\) cekung ke atas pada satu sisi dan cekung ke bawah pada sisi lainnya dari \(c\). Grafik dalam Gambar 11 menunjukkan sejumlah kemungkinan.
Gambar 11
Seperti yang mungkin anda terka, titik-titik di mana \(f''(x)=0\) atau \(f''(x)\) tidak ada merupakan calon-calon untuk titik balik. Kita gunakan kata calon secara sengaja karena sama halnya seperti calon untuk jabatan politik yang mungkin gagal untuk terpilih, begitu pula titik di mana \(f''(x)=0\) atau \(f''(x)\) tidak ada juga mungkin gagal menjadi suatu titik balik.
Pandang \(f(x)=x^4\), yang grafiknya diperlihatkan dalam Gambar 12. Benar bahwa \(f''(0)=0\), tetapi titik asal bukan titik balik. Tetapi dalam pencarian titik-titik balik, kita mungkin dengan mengenali titik-titik dengan \(f''(x)=0\). (dan di mana \(f''(x)=0\) tidak ada). Kemudian kita memeriksa apakah mereka benar-benar merupakan titik-titik balik.

Gambar 12
Lihat kembali pada grafik dalam Contoh 4. Kita akan melihat bahwa \(f(x)\) mempunyai tiga titik balik, yaitu \((-\sqrt{3},-\sqrt{3/4}); (0,0)\), dan \((\sqrt{3},\sqrt{3/4})\).
CONTOH 5:
Cari semua titik balik untuk \(F(x)=x^{1/3}+2\).
Penyelesaian:

Turunan kedua, \(F''(x)\), tidak pernah 0; tetapi gagal untuk ada di \(x = 0\). Titik \((0,2)\) adalah titik balik karena \(F''(x)>0\) untuk \(x < 0\) dan \(F''(x)<0\) untuk \(x > 0\). Grafik disketsakan dalam Gambar 13.

Gambar 13
Cukup sekian penjelasan mengenai kemonotonan dan kecekungan fungsi beserta contoh soal dan pembahasannya dalam artikel ini. Semoga bermanfaat.
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Challenges are what make life interesting; overcoming them is what makes life meaningful.
