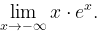www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Bentuk Tak Tentu › Limit Bentuk Nol Kali Tak Hingga
Limit Bentuk Nol Kali Tak Hingga
Kita dapat gunakan aturan I'Hopital pada bentuk ini tapi setelah kita mengubahnya menjadi bentuk tak tentu 0/0 atau ∞/∞.
Andaikan \(A(x)→0\), tetapi \(B(x)→∞\). Bagaimana dengan hasilkali \(A(x)⋅B(x)\)? Apakah akan menuju nol, ataukah tak terhingga atau apakah akan memiliki limit yang lain? Ini tergantung pada masing-masing \(A(x)\) dan \(B(x)\) yakni bagaimana caranya fungsi-fungsi ini menuju nol maupun tak-terhingga.
Lantas, apakah kita bisa menerapkan Aturan I'Hopital untuk kasus seperti ini yaitu untuk limit fungsi berbentuk \(A(x)⋅B(x)\)? Jawabannya adalah iya, tapi setelah kita mengubahnya menjadi bentuk tak tentu 0/0 atau \(∞/∞\).
CONTOH 1:
Carilah 
Penyelesaian:
Perhatikan bahwa
Jadi, limit yang harus kita cari berbentuk tak tentu \(0⋅∞\). Untuk menerapkan aturan I’Hopital, pertama kita perlu mengubahnya menjadi bentuk 0/0 dengan menulis \(\tan{x}\) sebagai \(1/\cot{x}\). Kita peroleh berikut ini,
Perhatikan bahwa kita menggunakan Aturan I’Hopital pada langkah kedua.
Contoh 2:
Hitunglah 
Pembahasan:
Perhatikan bahwa jika \(x=0\) disubstitusikan pada fungsi yang ada dalam limit, maka kita peroleh bentuk tantu \( 0 \cdot \infty \). Untuk mencari limit ini, kita ubah bentuk tersebut menjadi bentuk 0/0 atau ∞/∞. Dalam kasus ini, kita akan mengubahnya menjadi bentuk 0/0 dan kemudian menerapkan aturan I'Hopital.
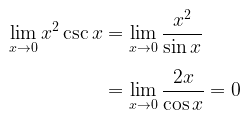
Contoh 3:
Hitunglah 
Pembahasan:
Perhatikan bahwa
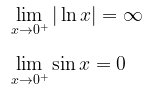
Jadi, kita peroleh bentuk tak tentu \( 0 \cdot \infty \).
Untuk mencari limit ini, kita ubah bentuk tersebut menjadi bentuk 0/0 atau ∞/∞. Dalam kasus ini, kita akan mengubahnya menjadi bentuk 0/0, yakni
Selanjutnya, kita akan menerapkan aturan I'Hopital.
Kita akan menggunakan aturan I'Hopital sekali lagi di sini.
Contoh 4:
Hitunglah 
Pembahasan:
Perhatikan bahwa jika \(x=0^+\) disubstitusikan pada fungsi yang ada dalam limit, maka kita peroleh bentuk tantu (0)(-∞). Untuk mencari limit ini, kita ubah bentuk tersebut menjadi bentuk 0/0 atau ∞/∞. Dalam kasus ini, kita akan mengubahnya menjadi bentuk ∞/∞ dan kemudian menerapkan aturan I'Hopital.
Contoh 5:
Hitunglah 
Pembahasan:
Perhatikan bahwa ini merupakan bentuk tantu (-∞)(0). Untuk mencari limit ini, kita ubah bentuk tersebut menjadi bentuk 0/0 atau ∞/∞. Pertama, kita akan coba mengubahnya menjadi bentuk 0/0 dan kemudian menerapkan aturan I'Hopital.
Seperti yang bisa Anda tebak bahwa ada yang aneh di sini. Tampaknya kita tidak akan mendapatkan jawaban yang diinginkan walaupun kita terus menggunakan aturan I'Hopital. Jika kondisi demikian terjadi, sebaiknya Anda berhenti sejenak dan mencoba cara lain yakni mengubahnya ke bentuk ∞/∞, alih-alih bentuk 0/0.
Dengan mengubah ke bentuk ∞/∞ dan menerapkan aturan I'Hopital maka diperoleh berikut ini.
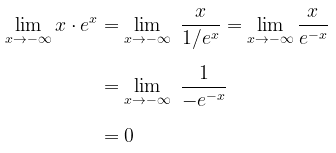
Sumber:
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Ketika seseorang menghina kamu, itu adalah sebuah pujian bahwa selama ini mereka menghabiskan banyak waktu untuk memikirkan kamu, bahkan ketika kamu tidak memikirkan mereka.