www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS I
Kalkulus I
Kalkulus I » Aplikasi Turunan › Teorema Nilai Rata-rata untuk Turunan
Turunan
Teorema Nilai Rata-rata untuk Turunan
Teorema Nilai Rata-rata mengatakan bahwa jika grafik sebuah fungsi kontinu mempunyai garis singgung tak vertikal pada setiap titik antara A dan B, maka terdapat paling sedikit satu titik C pada grafik antara A dan B sehingga garis singgung di titik C sejajar talibusur AB.
Oleh Tju Ji Long · Statistisi
Hub. WA: 0812-5632-4552
Salah satu aplikasi turunan adalah Teorema Nilai Rata-rata. Teorema ini mengatakan bahwa jika grafik sebuah fungsi kontinu mempunyai garis singgung tak vertikal pada setiap titik antara A dan B, maka terdapat paling sedikit satu titik C pada grafik antara A dan B sehingga garis singgung di titik C sejajar talibusur AB.
Dalam Gambar 1, hanya terdapat satu titik C yang demikian; dalam Gambar 2, terdapat beberapa.
Gambar 1.
Gambar 2.
Mari kita nyatakan Teorema ini dalam bahasa fungsi.
Teorema A: Teorema Nilai Rata-rata untuk Turunan
Jika \(f\) kontinu pada selang tertutup \([a,b]\) dan terdiferensial pada titik-titik dalam \((a,b)\), maka terdapat paling sedikit satu bilangan \(c\) dalam \((a,b)\) di mana
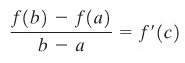
atau, secara setara, di mana
Contoh 1:
Cari bilangan \(c\) yang dijamin oleh Teorema Nilai Rata-rata untuk \(f(x)=2\sqrt{x}\) pada \([1,4]\).
Penyelesaian:
dan
Jadi, kita harus menyelesaikan
Jawaban tunggal adalah \(c = 9/4\) (Gambar 3)
Gambar 3
Contoh 2:
Andaikan \(f(x)=x^3-x^2-x+1\) pada \([-1,2]\). Cari semua bilangan \(c\) yang memenuhi kesimpulan terhadap Teorema Nilai Rata-rata.
Penyelesaian:
Gambar 4 menunjukkan grafik fungsi \(f\). Dari grafik ini, tampak bahwa terdapat dua bilangan \(c_1\) dan \(c_2\) dengan sifat yang disyaratkan.
Gambar 4
Sekarang kita menemukan
dan
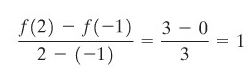
Jadi, kita harus menyelesaikan
dan
Dengan rumus abc untuk persamaan kuadrat, terdapat dua penyelesaian \((2±\sqrt{4+24})/6\) yang berpadanan terhadap \(c_1=-0,55\) dan \(c_2=1,22\). Kedua bilangan tersebut berada dalam selang \((-1,2)\).
Contoh 3:
Andaikan \(f(x)=x^{2/3}\) pada \([-8,27]\). Perlihatkan bahwa kesimpulan terhadap Teorema Nilai Rata-rata gagal dan jelaskan mengapa demikian.
Penyelesaian:
Perhatikan bahwa
dan
Jadi, kita harus menyelesaikan
dan
Tetapi \(c = 102\) tidak pada selang \((-8, 27)\) seperti disyaratkan. Seperti diperlihatkan oleh grafik \(y = f(x)\) pada Gambar 5, \(f'(0)\) gagal untuk terwujud, karena \(f(x)\) tidak terdiferensiasi di mana-mana pada \((-8, 27)\).
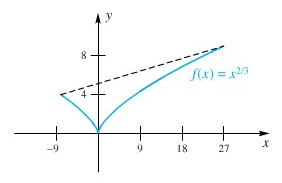
Gambar 5
Cukup sekian penjelasan mengenai teorema nilai rata-rata untuk turunan beserta contoh soal dan pembahasannya dalam artikel ini. Semoga bermanfaat.
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
If you cannot do great things, do small things in a great way.
Napoleon Hill