www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Teknik Pengintegralan › Teknik Integral Substitusi, Contoh Soal dan Pembahasan
Teknik Integral Substitusi, Contoh Soal dan Pembahasan
Untuk dapat menggunakan metode substitusi dengan hasil yang memuaskan, kita harus mengetahui integral-integral dalam bentuk baku sebanyak mungkin.
Pada artikel-artikel sebelumnya, kita telah belajar mengenai konsep dasar integral. Sekarang kita akan fokus pada teknik-teknik yang ada dalam menyelesaikan suatu integral.
Teknik-teknik tersebut meliputi teknik integral dengan substitusi, teknik integral parsial, teknik integral dengan pangkat trigonometri, teknik integral substitusi lain, dan terakhir teknik pengintegralan fungsi rasional yaitu hasil bagi dua fungsi suku banyak (polinom).
Pada artikel ini kita mulai dengan teknik integral substitusi, tetapi sebelum itu kita mengingat sedikit bentuk baku dalam integral agar memudahkan dalam menggunakan metode ini.
Bentuk Baku Integral
Untuk dapat menggunakan metode substitusi dengan hasil yang memuaskan, kita harus mengetahui integral-integral sebanyak mungkin. Beberapa daftar bentuk baku integral beserta hasilnya diberikan berikut ini. Daftar singkat ini sebaiknya dihafalkan karena akan membantu dalam menggunakan teknik integral dengan substitusi.

Substitusi dalam Integral Tak Tentu
Andaikan anda menghadapi suatu integral tak tentu. Apabila ini bentuk baku, segera dapatlah ditulis hasilnya. Apabila tidak, carilah sebuah substitusi yang akan mengubahnya menjadi suatu bentuk baku. Apabila pada substitusi yang pertama, kita tidak berhasil memperoleh bentuk baku, kita mencoba dengan cara lain. Setelah berlatih cukup lama, kita akan dapat menemukan penggantian yang tepat.
Teorema A: Aturan Substitusi dalam Integral Tak Tentu
Andaikan \(g\) adalah fungsi yang dapat didiferensialkan dan anggaplah bahwa \(F\) merupakan antiturunan dari \(f\). Maka, jika \(u = g(x)\),

CONTOH 1:

Penyelesaian:
Integral tersebut akan mengingatkan kita pada bentuk baku \(∫ \sec^2{u} \ du\). Sekarang andaikan \(u=x^2, du=2x \ dx\), sehingga

CONTOH 2:

Penyelesaian:
Ingatlah bentuk baku \(∫ \frac{du}{\sqrt{(a^2-u^2)}}\). Andaikan \(u=3x\), maka \(du=3 \ dx \). Sehingga

CONTOH 3:
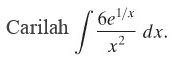
Penyelesaian:
Ingat bentuk baku \(∫ e^u du\). Andaikan \(u=1/x\), maka \(du=(-1/x^2) \ dx\). Sehingga

CONTOH 4:

Penyelesaian:
Ingatlah bentuk baku \(∫ \frac{1}{(a^2+u^2)} du\). Andaikan \(u = 3e^x\), maka \(du=3e^x \ dx\). Sehingga
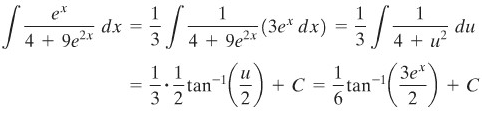
Tidak ada aturan yang mengharuskan kita menggunakan substitusi-\(u\). Jika kita dapat melakukan tanpa penggantian, lakukanlah. Dengan kata lain, kita tidak harus menuliskan substitusi-\(u\). Di bawah ini ada dua contoh yang kita maksudkan.
CONTOH 5:

Penyelesaian:
Dalam ingatan, substitusi \(u=x^2\).

CONTOH 6:

Penyelesaian:
Dalam ingatan, gunakan substitusi \(u = \tan{t}\).

Substitusi Dalam Integral Tentu
Substitsi dalam integral tentu sama seperti substitusi dalam integral tak tentu, tetapi kita tidak boleh lupa untuk mengubah batas-batas pengintegralannya.
Teorema B: Aturan Substitusi untuk Integral Tentu
Andaikan \(g\) mempunyai turunan yang kontinu pada \([a,b]\), dan andaikan \(f\) adalah kontinu pada range \(g\). Maka,

di mana \(u = g(x)\).
CONTOH 7:

Penyelesaian:
Andaikan \(u=t^2-4\), maka \(du=2t \ dt\). Perhatikan bahwa \(u=0\) jika \(t = 2\) dan \(u = 21\) jika \(t = 5\). Jadi,
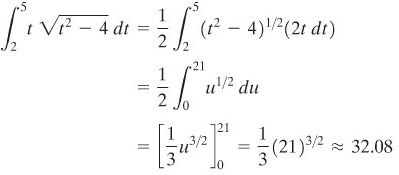
CONTOH 8:

Penyelesaian:
Dalam ingatan, substitusi \(u = x^4+11\). Kita peroleh

CONTOH 9:

Penyelesaian:
Misalkan \(u=x^2+2x+6\), sehingga \(du = (2x+2) \ dx = 2(x+1) \ dx\), dan perhatikan bahwa \(u = 6\) saat \(x = 0\) dan \(u = 9\) saat \(x = 1\). Dengan demikian,

Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Kindness is a language that the deaf can hear and the blind can see.
