Kalkulus I   »   Limit dan Kekontinuan   ›  Asimtot suatu Fungsi

Asimtot suatu Fungsi

Asimtot dari sebuah kurva adalah berupa sebuah garis yang sedemikian rupa sehingga jarak antara kurva dan garis tersebut mendekati nol seiring dengan salah satunya atau keduanya dari koordinat x atau y cenderung menuju tak hingga.

Dalam geometri analitis, asimtot (asymptote) dari sebuah kurva adalah berupa sebuah garis yang sedemikian rupa sehingga jarak antara kurva dan garis tersebut mendekati nol seiring dengan salah satunya atau keduanya dari koordinat x atau y cenderung menuju tak hingga (Sumber: Wikipedia).

Asimtot dapat dibedakan menjadi asimtot tegak (vertikal) dan asimtot mendatar (horizontal).

Garis \(x = c\) adalah asimtot vertikal dari grafik \(y = f(x)\) jika salah satu dari pernyataan-pernyataan berikut benar.

Perhatikan Gambar 1 di bawah. Garis \(x = 1\) pada kurva \( y = \frac{1}{(x-1)^2} \) adalah asimtot tegak atau asimtot vertikal.

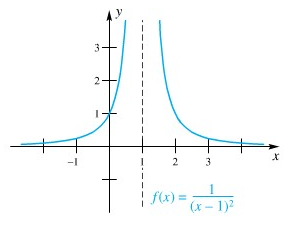
Gambar 1. Asimtot vertikal

Dalam nafas yang serupa, garis \(y = b\) adalah asimtot horisontal dari grafik \(y = f(x)\) jika

Garis \(y = 0\) pada Gambar 1 di atas adalah asimtot mendatar atau asimtot horisontal. Sama halnya, garis \(y = 2\) adalah asimtot horizontal pada Gambar 2 berikut.

Gambar 2. Asimtot horizontal

Sumber:

Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.

Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.