Kalkulus I   »   Fungsi   ›  Jenis-Jenis Fungsi

Jenis-Jenis Fungsi

Fungsi dapat diklasifikasikan ke dalam dua kelompok besar yakni fungsi aljabar dan fungsi transendental. Fungsi polinomial disebut fungsi aljabar, sedangkan fungsi yang selain fungsi aljabar disebut sebagai fungsi transendental

Secara umum, fungsi dapat diklasifikasikan ke dalam dua kelompok besar yakni fungsi aljabar dan fungsi transendental. Fungsi polinomial disebut fungsi aljabar, begitu pula dengan fungsi yang diperoleh darinya melalui penambahan, perkalian, pembagian, atau pengambilan pangkat dan akarnya.

Fungsi yang selain fungsi aljabar disebut sebagai fungsi transendental. Fungsi trigonometri, eksponensial, logaritma dan hiperbola serta invers dari fungsi-fungsi tersebut merupakan contoh fungsi transendental.

Mari kita bahas secara sekilas fungsi-fungsi tersebut.

Fungsi Linear

Fungsi dalam bentuk \(f(x) = mx+b\), untuk konstanta \(m\) dan \(b\), disebut fungsi linear. Gambar 1 menunjukkan beberapa garis \(f(x) = mx\) di mana \(b = 0\), sehingga garis-garis ini melewati titik asal (origin). Fungsi yang konstan dihasilkan ketika kemiringan \(m = 0\). (Gambar 2).

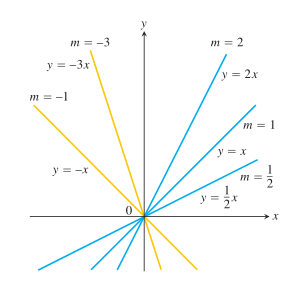
Gambar 1. Kumpulan garis \(y = mx\) mempunyai kemiringan \(m\) dan semua garis melewati titik asal (origin)

Gambar 2. Fungsi konstan mempunyai kemiringan \(m = 0\).

Fungsi Pangkat

Fungsi \(f(x)=x^a\), di mana \(a\) adalah sebuah konstanta, disebut fungsi pangkat. Ada beberapa hal penting yang perlu diperhatikan.

(a) \(a = n \ \), \(a\) bilangan bulat positif

Grafik \(f(x)=a^n\), untuk \(n = 1, 2, 3, 4, 5\) ditampilkan dalam Gambar 3. Fungsi-fungsi ini terdefinisi untuk semua bilangan riil \(x\). Perhatikan bahwa ketika pangkat n semakin besar, kurva cenderung mendatar terhadap sumbu-x pada interval (-1,1) dan juga naik lebih tajam untuk \(|x| > 1\). Tiap kurva melewati titik (1,1) dan melalui titik asal.

Gambar 3. Grafik \(f(x)=x^n \ ,n=1,2,3,4,5\) terdefinisi untuk \(-∞ < x < ∞\)

(b) \(a = -1\) atau \(a = -2\)

Grafik fungsi \(f(x)=x^{-1}=1/x\) dan \(g(x)=x^{-2}=1/x^2\) ditunjukkan dalam Gambar 4. Kedua fungsi terdefinisi untuk semua \(x≠0\) (Anda tidak akan pernah bisa membagi dengan nol). Grafik \(y = 1/x\) adalah hiperbola \(xy=1\) yang mendekati sumbu koordinat jauh dari titik asal. Grafik \(y=1/x^2\) juga mendekati sumbu koordinat.

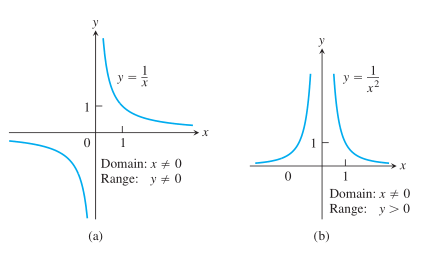
Gambar 4. Grafik fungsi pangkat \(f(x)=x^a\) untuk (a) \(a = -1\) dan (b) \(a = -2\).

(c) \(a = \frac{1}{2}, \frac{1}{3}, \frac{3}{2}\) dan \(\frac{2}{3}\)

Fungsi \(f(x)=x^{1/2}=\sqrt{x}\) dan \(g(x)=x^{1/3}=\sqrt[3]{x}\) adalah masing-masing fungsi akar kuadrat dan akar kubik. Domain atau daerah asal fungsi akar kuadrat adalah \([0,∞)\), tetapi fungsi akar kubik terdefinisi untuk semua bilangan riil \(x\). Grafiknya ditampilkan dalam Gambar 5 bersamaan dengan grafik \(y=x^{3/2}\) dan \(y=x^{2/3}\). (Ingat bahwa \(x^{3/2}=(x^{1/2})^3\) dan \(x^{2/3}=(x^{1/3})^2)\).

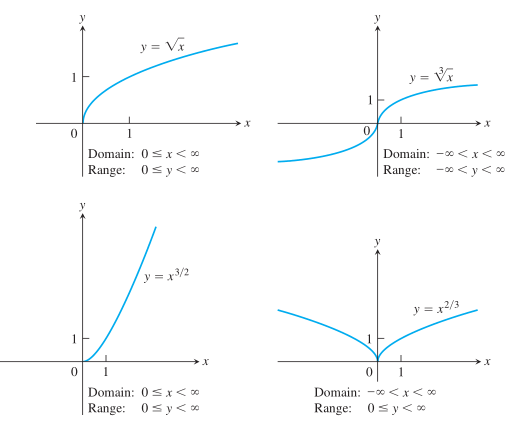
Gambar 5. Grafik fungsi pangkat \(f(x)=x^a\) untuk \(a = \frac{1}{2}, \frac{1}{3}, \frac{3}{2}\) dan \(\frac{2}{3}\)

Fungsi Polinomial

Fungsi \(p\) adalah fungsi polinomial jika

di mana \(n\) adalah bilangan bulat tak negatif dan bilangan \(a_0,a_1,a_2,…,a_n\) disebut koefisien polinomial. Semua polinomial mempunyai domain \((-∞,∞)\). Jika koefisien utama \(a_n≠0\) dan \(n > 0\), maka \(n\) disebut derajat polinomial. Fungsi linear dengan \(m≠0\) adalah polinomial dengan derajat 1. Polinomial derajat 2, biasanya dituliskan sebagai \(p(x)=ax^2+bx+c\), disebut fungsi kuadratik.

Demikian pula, fungsi kubik \(p(x)=ax^3+bx^2+cx+d\) adalah polinomial berderajat 3. Gambar 6 menunjukkan tiga grafik polinomial.

Gambar 6. Grafik tiga fungsi polinomial

Fungsi Rasional

Fungsi rasional merupakan hasilbagi atau rasio dua polinomial:

yang mana \(p\) dan \(q\) adalah polinomial. Domain fungsi rasional adalah himpunan semua bilangan riil \(x\) di mana \(q(x)≠0\). Sebagai contoh, fungsi

merupakan fungsi rasional dengan domain \(\{x|x≠-4/7\}\). Grafiknya ditunjukkan dalam Gambar 7 (a) dengan grafik dua fungsi rasional yang lainnya.

Gambar 7. Grafik tiga fungsi rasional

Fungsi Aljabar

Fungsi aljabar adalah fungsi yang dibangun dari fungsi polinomial dengan menggunakan operasi aljabar seperti penambahan, pengurangan, perkalian, pembagian, dan pengambilan akar. Fungsi rasional adalah kasus khusus fungsi aljabar. Gambar 8 di bawah menampilkan grafik tiga fungsi aljabar.

Gambar 8. Grafik tiga fungsi aljabar

Fungsi Trigonometri

Anda bisa mendapatkan bacaan lebih detail untuk fungsi trigonometri di link berikut. Grafik fungsi sinus dan cosinus ditunjukkan dalam Gambar 9.

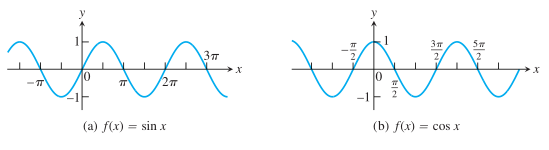
Gambar 9. Grafik sinus dan cosinus

Fungsi Eksponensial

Fungsi bentuk \(f(x)=a^x\), di mana basis \(a > 0\) adalah sebuah bilangan konstanta positif dan \(a≠1\), disebut fungsi eksponensial. Semua fungsi eksponensial mempunyai domain \((-∞,∞)\) dan range \((0,∞)\). Sehingga fungsi eksponensial tidak pernah mengasumsikan nilai 0. Grafik beberapa fungsi eksponensial ditunjukkan dalam Gambar 10.

Gambar 10. Grafik fungsi eksponensial

Fungsi logaritma

Fungsi bentuk \(f(x)=log_a⁡ x\), di mana basis \(a≠1\) adalah konstanta positif disebut fungsi logaritma. Fungsi ini merupakan fungsi invers dari fungsi eksponensial. Gambar 11 menunjukkan empat grafik fungsi logaritma dengan berbagai basis. Dalam tiap kasus domainnya adalah \((0,∞)\) dan range-nya adalah \((-∞,∞)\).

Gambar 11. Grafik fungsi logaritma

Fungsi Transendental

Fungsi yang selain fungsi aljabar disebut fungsi transendental, yang mencakup fungsi trigonometri, invers trigonometri, eksponensial, logaritma, hiperbola dan banyak fungsi lainnya.

Sebuah contoh fungsi transendental adalah catenary. Grafiknya berupa sebuah kabel, seperti saluran telepon atau kabel TV, digantung dari satu penyangga ke penyangga lain dan bergantung bebas di bawah bobotnya sendiri. Perhatikan Gambar 12.

Gambar 12. Grafik fungsi catenary

Sumber:

Anton, Howard., et al. (2012). Calculus, 10th ed. Hoboken: John Wiley & Sons, Inc.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.