www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Aplikasi Integral › Volume Benda Putar dengan Metode Kulit Tabung
Volume Benda Putar dengan Metode Kulit Tabung
Selain untuk mencari luas suatu daerah, integral juga digunakan untuk menghitung volume suatu benda. Terdapat beberapa cara untuk menghitung volume menggunakan integral, salah satu di antaranya yaitu metode tabung.
Selain untuk mencari luas suatu daerah, integral juga digunakan untuk menghitung volume suatu benda. Terdapat beberapa cara untuk menghitung volume menggunakan integral, salah satu di antaranya yaitu metode tabung.
Untuk berbagai persoalan, metode ini lebih mudah digunakan ketimbang metode cakram atau metode cincin yang telah kita bahas sebelumnya.
Kulit tabung di sini maksudnya adalah sebuah benda yang dibatasi oleh dua tabung lingkaran tegak yang sumbu simetrinya berimpit (Gambar 1). Apabila jari-jari tabung dalam adalah \(r_1\) dan jari-jari tabung luar adalah \(r_2\), sedangkan tinggi tabung adalah \(h\), maka volume kulit tabung adalah

Dengan demikian, kita peroleh


Gambar 1.
Ada cara mudah untuk mengingat rumus volume di atas. Perhatikan bahwa ketika kulit tabung itu kita potong sepanjang garis yang sejajar sumbu simetri dan kemudian membukanya, maka akan diperoleh selembar persegi-panjang yang memiliki ketebalan. Volume benda yang berbentuk lempeng ini dapat kita hitung (Gambar 2).

Gambar 2.
Sekarang perhatikanlah sebuah daerah seperti pada Gambar 3. Apabila kita potong-potong daerah tersebut sehingga terbentuk jalur-jalur vertikal dan kemudian diputar mengelilingi sumbu \(y\), maka akan terbentuk sebuah benda putar dan tiap jalur akan membentuk sebuah benda yang menyerupai suatu kulit tabung. Untuk memperoleh volume kulit tabung ini, kita hitung volume \(ΔV\) sesuatu kulit tabung, jumlahkan dan kemudian tarik limit jumlah ini apabila tebal kulit tabung makin menipis (menuju nol). Limit ini akan menghasilkan sebuah integral.

Gambar 3.
Untuk memahami apa yang dijelaskan di atas, perhatikanlah beberapa contoh berikut ini.
CONTOH 1:
Sebuah daerah yang dibatasi oleh kurva \(y=1/\sqrt{x}\), sumbu \(x\), garis \(y = 1\) dan garis \(x = 4\) diputar mengelilingi sumbu \(y\). Tentukan volume benda yang terbentuk!
Pembahasan:
Dari Gambar 3 di atas kita tahu bahwa volume kulit tabung yang dihasilkan oleh potongan-potongan adalah

yang mana, untuk \(y=1/\sqrt{x}\), menjadi
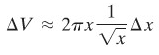
Volume benda kemudian dicari dengan pengintegralan.

CONTOH 2:
Sebuah daerah yang dibatasi oleh garis \(y=(r/h)x\), sumbu \(x\) dan garis \(x = h\) diputar mengelilingi sumbu \(x\) sehingga diperoleh sebuah kerucut (andaikan \(r>0, h>0\)). Tentukan volume kerucut itu dengan menggunakan metode cakram yang telah kita pelajari pada artikel sebelumnya dan metode kulit tabung.
Pembahasan:
(Metode Cakram). Ikutilah langkah-langkah pada Gambar 4.
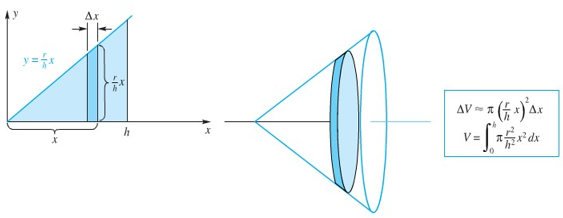
Gambar 4
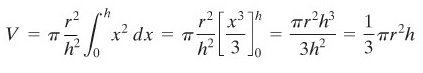
(Metode kulit tabung). Lihat Gambar 5.
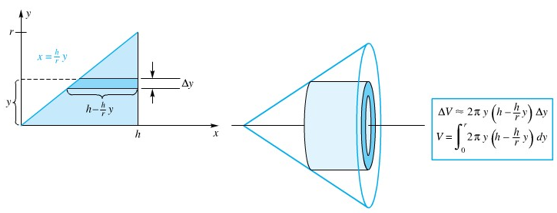
Gambar 5

Perhatikanlah bahwa kedua metode di atas menghasilkan rumus untuk volume kerucut yang telah kita pelajari saat di bangku sekolah menengah.
CONTOH 3:
Tentukan volume benda yang terbentuk apabila daerah pada kuadran pertama yang terletak di atas parabol \(y=x^2\) dan di bawah parabol \(y=2-x^2\), diputar mengelilingi sumbu \(y\).
Pembahasan:
Perhatikanlah Gambar 6 bagian kiri. Tampak bahwa penggunaan jalur-jalur datar bukanlah pilihan yang terbaik karena batas kanan terdiri atas bagian-bagian dari dua kurva, sehingga diperlukan dua integral. Untuk itu, lebih baik kita menggunakan jalur-jalur yang tegak dan kemudian gunakan metode kulit tabung untuk menghitung volume benda tersebut.


Gambar 6
Catatan:
Walaupun banyak di antara kita dapat melukiskan dengan baik sebuah gambar benda pada bidang (berdimensi dua), tidak banyak orang dapat menggambar benda-benda yang berdimensi tiga. Untungnya, kita tidak diharuskan untuk menggambar suatu benda terlebih dahulu untuk dapat menghitung volumenya. Biasanya sebuah gambar pada bidang dapat membantu asal kita memperoleh gambaran tentang benda ruang itu dalam pikiran kita.
Dalam contoh di bawah ini, kita bayangkan dalam pikiran kita sebuah benda yang diperoleh apabila daerah \(R\) pada Gambar 7 diputar mengelilingi berbagai sumbu putar. Tugas kita adalah membentuk sebuah integral untuk volume benda yang terbentuk, dengan menggunakan gambar pada bidang. Pelajarilah contoh ini dengan seksama.
CONTOH 4:
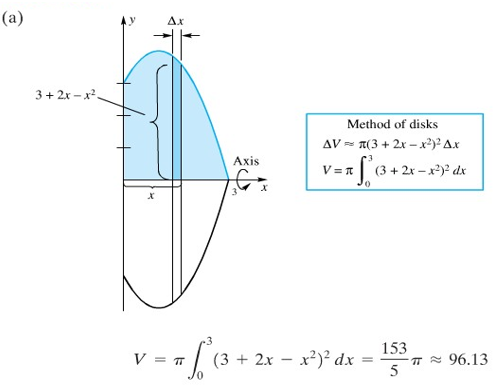
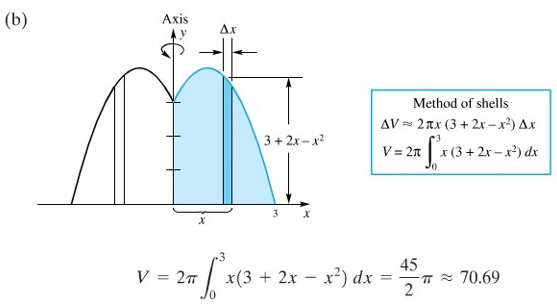
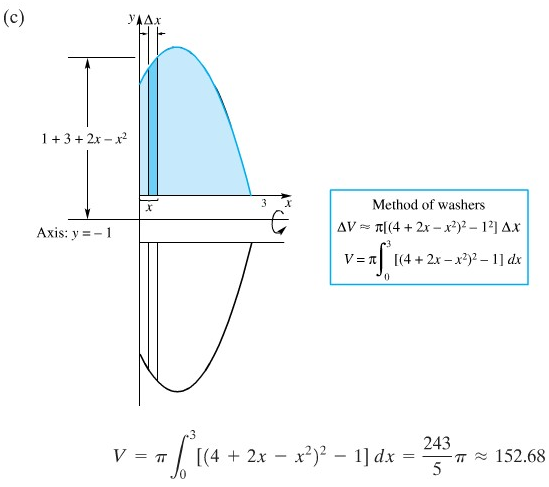
Bentuklah sebuah integral untuk volume benda yang terbentuk apabila daerah \(R\) yang ada pada Gambar 7 diputar mengelilingi: (a) sumbu \(x\); (b) sumbu \(y\); (c) garis \(y = -1\) dan (d) garis \(x = 4\).
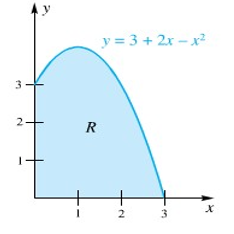
Gambar 7
Pembahasan:
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Change hurts. It makes people insecure, confused, and angry. People want things to be the same as they’ve always been, because that makes life easier.
