www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Limit dan Kekontinuan › Limit dan Kekontinuan
Limit dan Kekontinuan
Dalam bahasa yang biasa, kata kontinu digunakan untuk memeriksa suatu proses yang berkelanjutan tanpa perubahan yang mendadak.
Dalam bahasa yang biasa, kata kontinu digunakan untuk memeriksa suatu proses yang berkelanjutan tanpa perubahan yang mendadak. Gagasan inilah, yang berkenaan dengan fungsi, yang sekarang ingin dibuat secara persis.
Pandang tiga grafik yang diperlihatkan dalam Gambar 1. Hanya grafik yang ketiga memperlihatkan kekontinuan di \(c\).
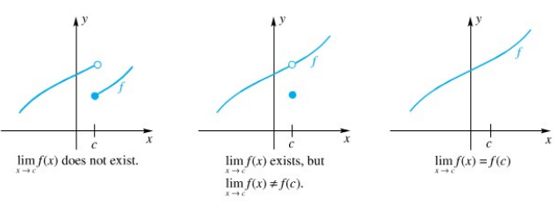
Gambar 1
Berikut adalah definisi yang formal.
DEFINISI: Kekontinuan di satu titik
Andaikan \(f\) terdefinisi pada sebuah selang terbuka yang mengandung \(c\). Kita katakan bahwa \(f\) kontinu di \(c\) jika

Dengan definisi ini kita bermaksud mensyaratkan tiga hal:
- \(\displaystyle{\lim_{x \to c}}\,f(x)\) ada
- \(f(c)\) ada (yakni, \(c\) berada dalam daerah asal \(f\)), dan
- \(\displaystyle{\lim_{x \to c}}\,f(x) = f(c)\)
Jika salah satu dari ketiga syarat tersebut tak terpenuhi, maka \(f\) takkontinu (diskontinu) di \(c\). Jadi, fungsi yang diwakili oleh grafik yang pertama dan kedua di atas takkontinu di \(c\), tetapi kontinu di titik-titik lain dari daerah asalnya.
CONTOH 1:
Andaikan \(f(x) = (x^2 - 4)/(x - 2), \ x ≠ 2\). Bagaimana seharusnya \(f\) didefinisikan di \(x = 2\) agar kontinu di titik itu?
Penyelesaian:

Karena itu, kita definisikan \(f(2) = 4\). Grafik dari fungsi yang didefinisikan diperlihatkan dalam Gambar 2. Kenyataannya, kita lihat bahwa \(f(x) = x + 2\) untuk semua x.

Gambar 2
Kekontinuan Beberapa Fungsi
TEOREMA A:
Fungsi polinom kontinu di setiap bilangan riil \(c\). Fungsi rasional kontinu di setiap bilangan riil \(c\) dalam daerah daerah asalnya, yaitu kecuali di mana penyebutnya adalah 0.
TEOREMA B:
Fungsi nilai mutlak adalah kontinu di setiap bilangan riil \(c\). Jika \(n\) ganjil, fungsi akar ke \(n\) kontinu di setiap bilangan riil \(c\); jika \(n\) genap fungsi ini kontinu di setiap bilangan riil positif \(c\).
Kekontinuan dalam Operasi Fungsi
TEOREMA C:
Jika \(f\) dan \(g\) kontinu di \(c\), maka demikian juga \(kf, \ f + g, \ f - g, \ f.g, \ f/g\) (asalkan \(g(c) ≠ 0\), \(f^n\), dan \(\sqrt[n]{f}\) (asalkan \(f(c) > 0\) jika \(n\) genap).
CONTOH 2:
Pada bilangan-bilangan berapa saja

kontinu?
Penyelesaian:
Kita tidak perlu memandang bilangan-bilangan tak positif, karena F tak terdefinisi di bilangan-bilangan yang demikian. Untuk setiap bilangan positif, fungsi-fungsi \(\sqrt{x}, \sqrt[3]{x}, |x| \), dan \(x^2\) semuanya kontinu (Teorema A dan B).
Menyusul dari Teorema C bahwasanya \(3|x|, 3|x| - x^2, \sqrt{x} + \sqrt{x}, \sqrt[3]{x},\) dan – akhirnya
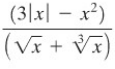
adalah kontinu di setiap bilangan positif.
TEOREMA D: Kontinuitas Fungsi Trigonometrik
Fungsi \(\sin\) dan \(\cos\) adalah kontinu di setiap bilangan riil \(c\). Fungsi \(\tan x, \ \cot x, \ \sec x\), dan \(\csc x\) adalah kontinu di setiap bilangan riil \(c\) pada daerah asalnya.
CONTOH 3:
Tentukan semua titik kekontinuan dari fungsi \(f(x) = \sin{x}/(x(1 - x)), x ≠ 0, 1\). Klasifikasikan masing-masing titik kekontinuan sebagai dapat dihapuskan atau tidak dapat dihapuskan (removable or nonremovable).
Penyelesaian:
Menurut Teorema D, pembilang adalah kontinu di setiap bilangan riil. Penyebut juga kontinu di setiap bilangan riil, tetapi saat \(x = 0\) atau \(x = 1\), penyebutnya adalah 0. Oleh karena itu, menurut Teorema C, f adalah kontinu di setiap bilangan rill kecuali pada \(x = 0\) dan \(x = 1\). Karena
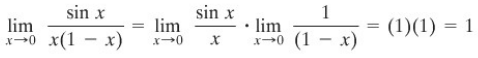
kita bisa mendefinisikan \(f(0) = 1\) dan fungsi akan kontinu di sana. Dengan demikian, \(x = 0\) adalah ketidakkontinuan yang dapat dihapuskan (a removable discontinuity). Juga, karena
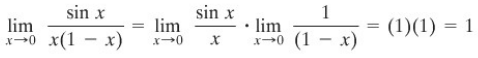
tidak ada cara untuk mendefinisikan \(f(1)\) untuk membuat \(f\) kontinu di \(x = 1\). Oleh karena itu, \(x = 1\) adalah ketidakkontinuan yang tidak dapat dihapuskan (a nonremovable discontinuity). Sebuah grafik \(y = f(x)\) ditunjukkan dalam Gambar 3.

Gambar 3
Terdapat operasi fungsi lain yang akan sangat penting dalam pekerjaan nantinya, yakni komposisi. Operasi ini juga mempertahankan kekontinuan.
TEOREMA E: Teorema limit komposit
Jika \(\displaystyle{\lim_{x \to c}}\,g(x)=L\) dan jika \(f\) kontinu di \(L\), maka

Khususnya, jika \(g\) kontinu di \(c\) dan \(f\) kontinu di \(g(c)\), maka fungsi komposit \(f \ o \ g\) kontinu di \(c\).
CONTOH 4:
Buktikan bahwa \(h(x) = |x^2 - 3x + 6|\) kontinu di setiap bilangan riil.
Penyelesaian:
Andaikan \(f(x) = |x|\) dan \(g(x) = |x^2 - 3x + 6|\). Keduanya kontinu di setiap bilangan riil, dan demikian juga dengan kompositnya.

CONTOH 5:
Tunjukkan bahwa

adalah kontinu kecuali di 3 dan \(-2\).
Penyelesaian:
\(x^2 - x - 6 = (x - 3)(x + 2)\). Oleh karena itu, fungsi rasional

adalah kontinu kecuali di 3 dan \(-2\) (Teorema A). Kita tahu dari Teorema D bahwa fungsi sin adalah kontinu di setiap bilangan riil. Oleh karena itu, dari Teorema E, kita simpulkan bahwa, karena \(h(x) = \sin{(g(x))}\), \(h\) juga kontinu kecuali di 3 dan \(-2\).
Kekontinuan pada selang
Sedemikian jauh, telah dibahas kekontinuan di suatu titik. Kita akan membahas kekontinuan pada suatu selang. Kekontinuan pada selang selayaknya berarti kekontinuan di setiap titik dari selang tersebut. Itulah tepatnya apa yang diartikan untuk suatu selang terbuka \((a,b)\).
Bilamana kita memandang selang tertutup \([a,b]\), kita menghadapi masalah. Mungkin saja \(f\) bahkan tidak terdefinisi di sebelah kiri \(a\) (misalnya, \(f(x) = \sqrt{x}\) mempunyai masalah ini di \(a = 0)\), sehingga secara langsung saja \(\displaystyle{\lim_{x \to a}}\,f(x)\) tidak ada.
Kita pilih untuk mengurus persoalan ini dengan menyebut \(f\) kontinu pada \([a,b]\) jika ia kontinu di setiap titik dari \((a,b)\) dan jika \(\displaystyle{\lim_{x \to a^+}}\,f(x) = f(a) \) dan \(\displaystyle{\lim_{x \to b^-}}\,f(x) = f(b) \) (masing-masing disebut, kekontinuan kanan di \(a\) dan kekontinuan kiri di \(b\)). Kita ringkaskan dalam sebuah definisi formal.
DEFINISI: Kekontinuan pada selang
Fungsi \(f\) adalah kontinu kanan di \(a\) jika \(\displaystyle{\lim_{x \to a^+}}\,f(x) = f(a)\) dan kontinu kiri di \(b\) jika \(\displaystyle{\lim_{x \to b^-}}\,f(x) = f(b)\).
Kita katakan \(f\) adalah kontinu pada selang terbuka \((a, b)\) jika \(f\) kontinu pada setiap titik \((a, b)\) dan \(f\) kontinu pada selang tertutup \([a, b]\) jika \(f\) kontinu pada \((a, b)\), kontinu kanan di \(a\), dan kontinu kiri di \(b\).
Sebagai contoh, pernyataan bahwa \(f(x) = 1/x\) kontinu pada \((0, 1)\) dan bahwa \(g(x) = \sqrt{x}\) kontinu pada \([0, 1]\) adalah benar.
CONTOH 6:
Dengan menggunakan definisi di atas, uraikan sifat-sifat kekontinuan dari fungsi yang grafiknya disketsakan dalam Gambar 4.

Gambar 4
Penyelesaian:
Fungsi itu kontinu pada selang terbuka \((-∞, 0), \ (0, 3)\), dan \((5, ∞)\) dan juga pada selang tertutup \([3, 5]\).
TEOREMA F: Teorema Nilai Antara
Jika \(f\) kontinu pada \([a, b]\) dan jika \(W\) sebuah bilangan antara \(f(a)\) dan \(f(b)\) maka terdapat sebuah bilangan \(c\) di antara \(a\) dan \(b\), sedemikian sehingga \(f(c) = W\).
Gambar 5 menunjukkan grafik fungsi \(f(x)\) yang kontinu pada \([a, b]\). Teorema Nilai Antara mengatakan bahwa untuk setiap \(W\) dalam \((f(a), f(b))\) pasti ada sebuah nilai \(c\) pada \([a, b]\) sehingga \(f(c) = W\).
Dengan kata lain, \(f\) mengambil setiap nilai antara \(f(a)\) dan \(f(b)\). Kekontinuan diperlukan untuk teorema ini, jika tidak demikian mungkin akan ditemukan sebuah fungsi \(f\) dan bilangan \(W\) antara \(f(a)\) dan \(f(b)\) di mana tidak terdapat \(c\) dalam \([a, b]\) yang memenuhi \(f(c) = W\).
Gambar 6 menunjukkan sebuah contoh untuk fungsi tersebut.
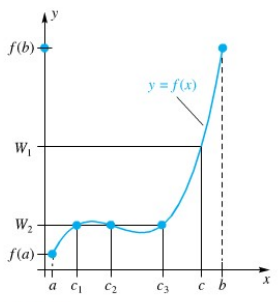
Gambar 5.

Gambar 6.
Kebalikan dari teorema ini, yang mana tidak benar secara umum, mengatakan bahwa jika \(f\) mengambil setiap nilai antara \(f(a)\) dan \(f(b)\) maka \(f\) adalah kontinu. Gambar 5 dan 7 menunjukkan fungsi yang mengambil semua nilai antara \(f(a)\) dan \(f(b)\), tetapi fungsi dalam gambar 7 tidak kontinu pada \([a, b]\). Hanya karena sebuah fungsi mempunyai sifat nilai antara, itu tidak berarti bahwa fungsi tersebut kontinu.
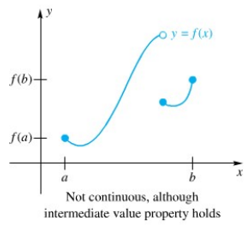
Gambar 7
CONTOH 7:
Gunakan Teorema Nilai Antara untuk menunjukkan bahwa persamaan \(x-\cosx=0\) mempunyai sebuah solusi antara \(x = 0\) dan \(x = π/2\).
Penyelesaian:
Andaikan \(f(x) = x - \cos{x}\), dan misalkan \(W = 0\). Maka \(f(0) = 0 - \cos{0} = -1\) dan \(f(π/2) = π/2 - \cos π/2 = π/2\). Karena \(f\) kontinu pada \([0, π/2]\) dan W = 0 berada antara \(f(0)\) dan \(f(π/2)\), Teorema Nilai Antara mengimplikasikan kehadiran sebuah \(c\) pada interval (0, π/2) dengan sifat bahwa \(f(c) = 0\). Nilai \(c\) tersebut merupakan sebuah solusi untuk persamaan \(x - \cos{x} = 0\). Gambar 8 menyarankan bahwa terdapat satu nilai \(c\).
Kita bisa meneruskan satu langkah lebih lanjut. Titik tengah interval \([0, π/2]\) adalah titik \(x = π/4\). Saat kita mengevaluasi \(f(π/4)\), kita peroleh
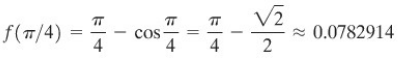
yang lebih besar dari 0. Dengan demikian, \(f(0) < 0\) dan \(f(π/4) > 0\), sehingga aplikasi lain dari Teorema Nilai Antara memberitahu kita bahwa terdapat sebuah \(c\) antara 0 dan π/4 sehingga \(f(c) = 0\).

Gambar 8
Cukup sekian penjelasan mengenai limit dan kekontinuan beserta contoh soal dan pembahasannya dalam artikel ini. Semoga bermanfaat.
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Live as if you were to die tomorrow. Learn as if you were to live forever.
