Kalkulus I   »   Bentuk Tak Tentu   ›  Limit Bentuk Nol Pangkat Nol

Limit Bentuk Nol Pangkat Nol

Bentuk tak tentu jenis eksponen yang lainnya berbentuk nol pangkat nol. Cara yang kita pakai ialah menulis bentuk tak tentu tersebut sebagai logaritma. Kemudian Aturan I’Hopital kita gunakan pada bentuk logaritma ini.

Bentuk tak tentu jenis eksponen yang lainnya berbentuk \(0^0\). Cara yang kita pakai untuk menyelesaikan bentuk tak tentu ini sama dengan bentuk eksponen yang telah kita bahas sebelumnya (bentuk \(1^∞\)) yaitu dengan menulis bentuk tak tentu tersebut sebagai logaritma, kemudian menerapkan Aturan I’Hopital pada bentuk logaritma tersebut.

Untuk lebih jelasnya, perhatikanlah contoh berikut ini.

CONTOH 1:

Diketahui \( f(x) = (x-π)^{\tan{⁡x}} \). Tentukan \( \displaystyle{\lim_{x→π^+} f(x)} \) !

Penyelesaian:

Bentuk tersebut adalah bentuk tak-tentu \(0^0\), sehingga

Note: * limit bernilai 0/0 sehingga Aturan I’Hopital dapat diterapkan.

CONTOH 2:

Jika diketahui \(f(x)=(x+\sin{⁡x})^x\), tentukan \( \displaystyle{\lim_{x→0^+} f(x)} \)!

Penyelesaian:

Bentuk tersebut adalah bentuk tak-tentu \(0^0\), sehingga

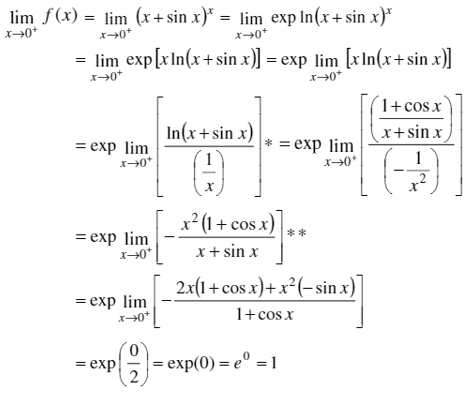
Note: * limit bernilai \(∞/∞\) dan ** berbentuk 0/0 sehingga Aturan I’Hopital dapat diterapkan.

CONTOH 3:

Hitunglah \( \displaystyle{\lim_{x→0^+} (\tan{x})^{\sin{x}} } \)!

Penyelesaian:

Bentuk tersebut adalah bentuk tak-tentu \(0^0\), sehingga

Note: * limit bernilai \(∞/∞\) sehingga Aturan I’Hopital dapat diterapkan.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.