www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Integral › Sifat-Sifat Integral
Sifat-Sifat Integral
Terdapat suatu cara yang lebih baik dalam menghitung integral tentu; yaitu dengan memahami sifat-sifat yang melekat padanya.
Kita telah mampu menghitung beberapa integral tentu dari definisi secara langsung berkat adanya rumus-rumus manis untuk \(1 + 2 + 3+ …+ n\), \(1^2+2^2+⋯+n^2\), dan seterusnya.
Penghitungan integral tentu dengan cara ini selalu membosankan, biasanya sukar, dan kadang-kadang praktis tidak mungkin. Untung saja terdapat suatu cara yang lebih baik dalam menghitung integral tentu; yaitu yang akan menjadi pokok bahasan pada bagian ini.
TEOREMA A: Teorema Dasar Kalkulus
Andaikan \(f\) kontinu (karenanya terintegralkan) pada \([a,b]\) dan andaikan \(F\) sebarang anti turunan dari \(f\) di sana. Maka,

CONTOH 1:
Perlihatkan bahwa

di mana \(k\) adalah konstanta.
Penyelesaian:
\(F(x)=kx\) adalah suatu anti turunan dari \(f(x)=k\). Sehingga menurut Teorema Dasar,

CONTOH 2:
Perlihatkan bahwa

Penyelesaian:
\(F(x)=x^2/2\) adalah suatu anti turunan dari \(f(x)=x\). Karena itu,

CONTOH 3:
Perlihatkan bahwa jika \(r\) suatu bilangan rasional yang bukan \(–1\), maka
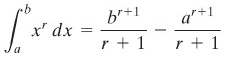
Penyelesaian:
\(F(x)=x^{(r+1)}/(r+1)\) adalah suatu anti turunan dari \(f(x)=x^r\). Maka, menurut Teorema Dasar,

Adalah menguntungkan untuk memperkenalkan lambang baru untuk \(F(b)-F(a)\). Kita tuliskan
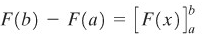
Perhatikan contohnya berikut ini.

TEOREMA B: Kelinearan Integral Tentu
Andaikan \(f\) dan \(g\) terintegralkan pada \([a,b]\) dan bahwa \(k\) konstanta. Maka \(kf\) dan \(f+g\) adalah teintegralkan dan

CONTOH 4:
Hitunglah integral \( \int_\limits{-1}^2 (4x-6x^2) \ dx \) dengan menggunakan sifat kelinearan pada Teorema B.
Penyelesaian:

TEOREMA C: Sifat Penambahan Selang
Jika \(f\) terintegralkan pada suatu selang yang mengandung tiga titik \(a, b\), dan \(c\), maka

bagaimanapun urutan dari \(a, b\), dan \(c\).
Misalnya, \( \int_0^2 x^2 \ dx \) dapat dinyatakan sebagai

TEOREMA D: Sifat Pembandingan
Jika \(f\) dan \(g\) terintegralkan pada \([a,b]\) dan jika \(f(x)≤g(x)\) untuk semua \(x\) dalam \([a,b]\), maka
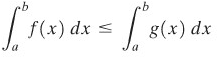
TEOREMA E: Sifat Keterbatasan
Jika \(f\) terintegralkan pada \([a,b]\) dan jika \(m≤f(x)≤M\) untuk semua \(x\) dalam \([a,b]\), maka

TEOREMA F: Pendiferensialan suatu integral tentu
Andaikan f kontinu pada selang tertutup [a,b] dan andaikan x sebuah (variabel) titik dalam [a,b]. Maka,

CONTOH 5:

Penyelesaian:
Menurut Teorema F, kita peroleh

CONTOH 6:
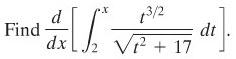
Penyelesaian:
Menurut Teorema F, kita peroleh
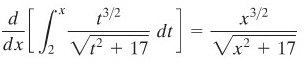
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Ia yang mengerjakan lebih dari apa yang dibayar pada suatu saat akan dibayar lebih dari apa yang ia kerjakan.
