www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Aplikasi Turunan › Aplikasi Turunan: Maksimum dan Minimum Lokal
Aplikasi Turunan: Maksimum dan Minimum Lokal
Nilai maksimum global merupakan yang terbesar di antara nilai-nilai maksimum lokal. Demikian pula nilai minimum global adalah yang terkecil di antara nilai-nilai minimum lokal.
Dari pembahasan mengenai nilai maksimum dan minimum pada tulisan sebelumnya, kita tahu bahwa nilai maksimum (jika ada) suatu fungsi \(f\) pada himpunan \(S\) adalah nilai \(f\) terbesar yang dicapai pada keseluruhan himpunan \(S\). Kadang-kadang diacu sebagai nilai maksimum global, atau nilai maksimum absolut dari \(f\).
Jadi, untuk fungsi \(f\) dengan daerah asal \(S = [a,b]\) yang grafiknya diberikan dalam Gambar 1, \(f(a)\) adalah nilai maksimum global.
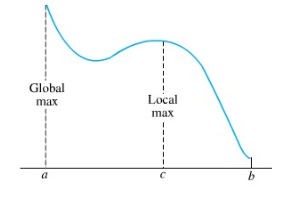
Gambar 1
Akan tetapi, bagaimana dengan \(f(c)\)? Mungkin saja ia bukan raja dari negara, tetapi paling tidak ia adalah kepala dari lingkungan sekitarnya. Kita sebut \(f(c)\) suatu nilai maksimum lokal, atau nilai maksimum relatif. Tentu saja nilai maksimum global otomatis juga nilai maksimum lokal. Gambar 2 melukiskan sejumlah kemungkinan.

Gambar 2
Perhatikan bahwa nilai maksimum global (jika ada) merupakan yang terbesar di antara nilai-nilai maksimum lokal. Demikian pula nilai minimum global adalah yang terkecil di antara nilai-nilai minimum lokal.
Berikut definisi formal dari maksimum dan minimum lokal. Ingat kembali bahwa lamba \(∩\) menyatakan irisan (bagian bersama) dari dua himpunan.
Definisi: Maksimum dan Minimum Lokal
Andaikan \(S\), daerah asal \(f\), memuat titik \(c\). Kita katakan bahwa
- \(f(c)\) nilai maksimum lokal \(f\) jika terdapat selang \((a,b)\) yang memuat \(c\) sedemikian sehingga \(f(c)\) adalah nilai maksimum \(f\) pada \((a,b) ∩ S\);
- \(f(c)\) nilai minimum lokal \(f\) jika terdapat selang \((a,b)\) yang memuat \(c\) sedemikian sehingga \(f(c)\) adalah nilai minimum \(f\) pada \((a,b) ∩ S\);
- \(f(c)\) adalah nilai ekstrim lokal \(f\) jika ia berupa nilai maksimum lokal atau minimum lokal.
Di mana Nilai-nilai Ekstrem Lokal Terjadi?
Teorema Titik Kritis berlaku sebagaimana dinyatakan, dengan ungkapan nilai ekstrim diganti oleh nilai ekstrim lokal, bukti pada dasarnya sama. Jadi, titik-titik kritis (titik ujung, titik stasioner, dan titik singular) adalah calon untuk titik tempat kemungkinan terjadinya ekstrim lokal.
Kita katakan calon karena kita tidak menuntut bahwa setiap titik kritis harus merupakan ekstrim lokal. Bagian kiri grafik dalam Gambar 3 membuat ini jelas. Tetapi, jika turunan adalah positif pada salah satu pihak dari titik kritis dan negatif pada pihak lainnya, maka kita mempunyai ekstrim lokal.

Gambar 3.
Teorema A: Uji Turunan Pertama
Andaikan \(f\) kontinu pada selang terbuka \((a,b)\) yang memuat titik kritis \(c\).
- Jika \(f'(x)>0\) untuk semua \(x\) dalam \((a, c)\) dan \(f'(x)<0\) untuk semua \(x\) dalam \((c,b)\), maka \(f(c)\) adalah nilai maksimum lokal \(f\).
- Jika \(f'(x)<0\) untuk semua \(x\) dalam \((a,c)\) dan \(f'(x)>0\) untuk semua \(x\) dalam \((c,b)\), maka \(f(c)\) adalah nilai minimum lokal \(f\).
- Jika \(f'(x)\) bertanda sama pada kedua pihak \(c\), maka \(f(c)\) bukan nilai ekstrim lokal \(f\).
Contoh 1:
Cari nilai ekstrim lokal dari fungsi \(f(x)=x^2-6x+5\), pada \((-∞,∞)\).
Penyelesaian:
Fungsi polinom \(f\) kontinu di mana-mana, dan turunannya, \(f'(x)=2x-6\), ada untuk semua \(x\). Jadi, satu-satunya titik kritis untuk \(f\) adalah penyelesaian tunggal dari \(f'(x)=0\), yakni \(x = 3\).
Karena \(f'(x)=2 (x-3)<0\) untuk \(x < 3\), \(f\) turun pada \((-∞,3]\); dan karena \(2 (x – 3 ) > 0\) untuk \(x > 3\), \(f\) naik pada \([3,∞)\). Karena itu, menurut Uji Turunan Pertama, \(f(3) = -4\) adalah nilai minimum lokal \(f\). Karena 3 adalah satu-satunya bilangan kritis, tidak terdapat nilai ekstrim lain. Grafik \(f\) diperlihatkan dalam Gambar 4. Perhatikan bahwa dalam kasus ini \(f(3)\) sebenarnya adalah nilai minimum (global).
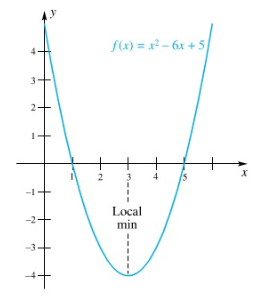
Gambar 4
Contoh 2:
Cari nilai ekstrim lokal dari \(f(x)= \frac{1}{3} x^3-x^2-3x+4\) pada \((-∞,∞)\).
Penyelesaian:
Karena \(f'(x)=x^2-2x-3=(x+1)(x-3)\), titik kritis \(f\) hanyalah -1 dan 3. Bilamana kita gunakan titik-titik uji – 2, 0, dan 4, kita pahami bahwa \((x+1)(x-3) > 0\) pada \((-∞,-1)\) dan \((3,∞)\) dan \((x+1)(x-3)<0\) pada \((-1,3)\). Menurut Uji Turunan Pertama, kita simpulkan bahwa \(f(-1)=17/3\) adalah nilai maksimum lokal dan bahwa \(f(3) = - 5\) adalah nilai minimum lokal (Gambar 5).

Gambar 5
Contoh 3:
Cari nilai ekstrim lokal dari \(f(x)=(\sinx)^{2/3}\) pada \((-π/6,2π/3)\).
Penyelesaian:
Titik 0 dan \(π/2\) adalah titik-titik kritis karena \(f'(0)\) tidak ada dan \(f'(π/2)=0\). Sekarang \(f'(x) < 0\) pada \((-π/6,0)\) dan pada \((π/2,2π/3)\), sedangkan \( f'(x)>0 \) pada \((0,π/2)\). Menurut Uji Turunan Pertama kita simpulkan bahwa \(f(0)=0\) adalah nilai minimum lokal dan bahwa \(f(π/2)=1\) adalah nilai maksimum lokal. Grafik \(f\) diperlihatkan pada Gambar 6.

Gambar 6
Uji Turunan Kedua
Terdapat uji lain untuk maksimum dan minimum lokal yang kadang-kadang lebih mudah diterapkan daripada Uji Turunan Pertama. Ia menyangkut penghitungan turunan kedua pada titik-titik stasioner. Ia tidak berlaku pada titik singular.
Teorema B: Uji Turunan Kedua
Andaikan \(f'\) dan \(f''\) ada pada setiap titik dalam selang terbuka \((a,b)\) yang memuat \(c\), dan andaikan \(f'(c)=0\).
- Jika \(f''(c)<0\), maka \(f(c)\) adalah nilai maksimum lokal \(f\).
- Jika \(f''(c)>0\), maka \(f(c)\) adalah nilai minimum lokal \(f\).
Contoh 4:
Untuk \(f(x)=x^2-6x+5\), gunakan Uji Turunan Kedua untuk mengenali ekstrim lokal.
Penyelesaian:
Ini adalah fungsi dari Contoh 1. Perhatikan bahwa
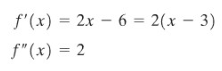
Jadi, \(f'(3)=0\) dan \(f''(3)>0\). Karena itu, menurut Uji Turunan Kedua, \(f(3)\) adalah nilai minimum lokal.
Contoh 5:
Untuk \(f(x)= \frac{1}{3} x^3-x^2-3x+4\), gunakan Uji Turunan Kedua untuk mengenali ekstrim lokal.
Penyelesaian:
Ini adalah fungsi dari Contoh 2. Perhatikan bahwa
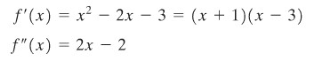
Titik-titik kritis adalah – 1 dan 3 \((f'(-1)=f'(3)=0)\). Karena \(f''(-1)=-4\) dan \(f''(3)=4\), kita simpulkan menurut Uji Turunan Kedua – bahwa \(f(-1)\) adalah nilai maksimum lokal dan bahwa \(f(3)\) adalah nilai minimum lokal.
Sayang, Uji Turunan Kedua kadang-kadang gagal, karena \(f''(x)\) mungkin 0 pada titik stasioner. Untuk \(f(x)=x^3\) dan \(f(x)=x^4\), \(f'(0)=0\) dan \(f''(0)=0\) (lihat Gambar 7). Yang pertama tidak mempunyai nilai maksimum atau minimum lokal di 0; yang kedua mempunyai minimum lokal di sana. Ini memperlihatkan bahwa jika \(f''(x)=0\) di titik stasioner, kita tidak mampu menarik kesimpulan tentang maksimum atau minimum tanpa informasi tambahan.

Gambar 7.
Ekstrim pada Selang Terbuka
Masalah yang kita pelajari dalam Optimisasi Fungsi: Maksimum dan Minimum, biasanya menganggap bahwa himpunan pada mana kita ingin memaksimumkan atau meminimumkan suatu fungsi berupa selang tertutup.
Tetapi, selang-selang yang muncul dalam praktek tidak selalu tertutup; kadang-kadang terbuka atau bahkan setengah terbuka, setengah tertutup. Kita masih tetap menangani masalah ini jika kita menerapkan secara benar teori yang dikembangkan dalam bagian ini. Ingat dalam hati bahwa maksimum (minimum) tanpa kata sifat tambahan berarti maksimum (minimum) global.
Kita berikan dua contoh untuk melukiskan prosedur yang sesuai untuk selang terbuka atau setengah terbuka.
Contoh 6:
Cari (jika mungkin) nilai maksimum dan minimum dari \(f(x)=x^4-4x\) pada \((-∞,∞)\).
Penyelesaian:
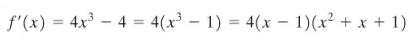
Karena \(x^2+x+1=0\) tidak mempunyai penyelesaian bilangan riil (rumus kuadrat), hanya terdapat satu titik kritis, yaitu \(x = 1\). Untuk \(x < 1\), \(f'(x)<0\), sedang untuk \(x > 1,\ f'(x)>0\). Kita simpulkan bahwa \(f(1)=-3\) adalah nilai minimum lokal untuk \(f\); dan karena \(f\) turun di sebelah kiri 1 dan naik di sebelah kanan 1, memang benar merupakan nilai minimum dari \(f\).
Fakta-fakta yang dinyatakan di atas menunjukkan bahwa \(f\) tidak dapat mempunyai nilai maksimum. Grafik \(f\) diperlihatkan dalam Gambar 8.
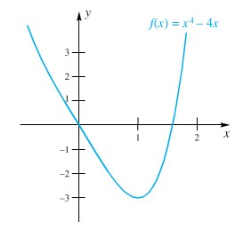
Gambar 8.
Cukup sekian penjelasan mengenai maksimum dan minimum lokal pada suatu fungsi beserta contoh soal dan pembahasannya dalam artikel ini. Semoga bermanfaat.
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
It is not what we get. But who we become, what we contribute…that gives meaning to our lives.
