www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Aplikasi Integral › Volume Benda Putar dengan Metode Cakram
Volume Benda Putar dengan Metode Cakram
Selain untuk mencari luas suatu daerah, integral juga digunakan untuk menghitung volume suatu benda. Terdapat beberapa cara untuk menghitung volume menggunakan integral, salah satu di antaranya yaitu metode cakram.
Selain untuk mencari luas suatu daerah, integral juga digunakan untuk menghitung volume suatu benda. Terdapat beberapa cara untuk menghitung volume menggunakan integral, salah satu di antaranya yaitu metode cakram.
Mari kita mulai dengan sebuah pertanyan. Apakah yang disebut volume? Perhatikanlah Gambar 1 yang menunjukkan empat benda.

Gambar 1.
Dalam tiap kasus, benda itu diperoleh dengan cara menggerakkan suatu daerah pada bidang sejauh \(h\) dengan arah yang tegak lurus pada daerah tersebut. Dalam tiap kasus itu, volume benda ditentukan sebagai luas A (daerah alas) dikalikan dengan tinggi \(h\), yakni \[ V = A \cdot h\]
Sekarang perhatikanlah sebuah benda di mana penampang-penampang tegak lurusnya pada suatu garis yang memiliki luas tertentu. Misalnya garis tersebut adalah sumbu \(x\) dan andaikan bahwa luas penampang di \(x\) adalah \(A(x)\) dengan \(a≤x≤b\) (Gambar 2).

Gambar 2.

Gambar 3.
Selang \([a,b]\) kita bagi dengan titik-titik bagi \(a=x_0 < x_1 < x_2 <⋯< x_n=b\). Melalui titik-titik itu kita lukis bidang tegak lurus pada sumbu \(x\). Dengan demikian kita peroleh pemotongan benda menjadi lempengan yang tipis-tipis (Gambar 3). Volume \(ΔV_i\) suatu lempeng dapat dianggap sebagai volume tabung, yaitu
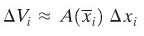
dan volume \(V\) benda dapat diaproksimasi dengan jumlah Riemann

Apabila norma partisi kita tujukan ke nol, kita peroleh suatu integral tentu; integral ini kita definisikan sebagai volume benda

Dalam perhitungan volume-volume benda, sebaiknya anda jangan menggunakan rumus itu secara hafalan. Akan tetapi, pahamilah proses yang menuju ke penemuan rumus tersebut. Seperti untuk luas, proses itu kita sebut pula, pemotongan, aproksimasi dan pengintegralan. Hal ini diperjelas dalam contoh-contoh di bawah ini.
Benda Putar: Metode Cakram.
Apabila sebuah daerah rata, yang terletak seluruhnya pada satu bagian bidang yang terbagi oleh sebuah garis lurus tetap, diputar mengelilingi garis tersebut, daerah itu akan membentuk sebuah benda putar. Garis yang tetap tersebut dinamakan sumbu putar.
Sebagai contoh, apabila daerah yang dibatasi oleh setengah lingkaran dan garis tengahnya, diputar mengelilingi garis tengah itu, maka daerah tersebut membentuk sebuah bola. Apabila daerah segitiga diputar mengelilingi salah satu kakinya, daerah itu akan membentuk sebuah kerucut (Gambar 4). Apabila sebuah daerah lingkaran diputar mengelilingi sebuah garis pada bidang lingkaran itu yang tidak memotongnya (Gambar 5), maka diperoleh sebuah torus (ban). Dalam tiap hal, volume benda-benda itu dapat disajikan sebagai suatu integral tentu.

Gambar 4.

Gambar 5.
CONTOH 1:
Tentukan volume benda putar yang dibentuk oleh daerah \(R\) yang dibatasi oleh kurva \(y=\sqrt{x}\), sumbu \(x\) dan garis \(x = 4\) apabila \(R\) diputar mengelilingi sumbu \(x\).
Pembahasan:
Daerah R dan volume benda putar diperlihatkan pada Gambar 6.

Gambar 6.
Pada bagian kiri Gambar 6 kita lihat daerah dengan sebuah jalur pemotongan. Apabila \(R\) diputar mengelilingi sumbu \(x\), daerah ini akan membentuk sebuah benda putar dan jalur tersebut membentuk sebuah cakram yang volumenya \(ΔV\) dapat kita aproksimasi dengan volume sebuah tabung dengan tinggi \(Δx_i\) dan dengan jari-jari alas \(\sqrt{x}\) sehingga, \(ΔV ≈ π \ (\sqrt{x})^2 \ Δx\), volume tabung ini adalah \(πr^2 h\). Apabila volume tabung-tabung ini kita jumlahkan dan kemudian kita integralkan, maka kita peroleh volume benda putar tersebut, yakni
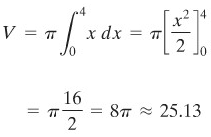
CONTOH 2:
Tentukan volume benda putar yang terbentuk apabila daerah yang dibatasi oleh kurva \(y=x^3\), sumbu \(y\) dan garis \(y = 3\) diputar mengelilingi sumbu \(y\). (Gambar 7).

Gambar 7.
Pembahasan:
Dalam kasus ini, lebih mudah jika y digunakan sebagai variabel pengintegralan. Perhatikan bahwa \(y=x^3\) setara dengan \(x=\sqrt[3]{y}\) dan \(ΔV ≈ π \ (\sqrt[3]{y})^2 \ Δy\). Dengan demikian, volume benda putar tersebut dapat dihitung sebagai berikut.

Benda Ruang Lain yang Penampangnya Diketahui.
Sejauh ini benda yang kita bahas memiliki daerah-daerah lingkaran sebagai penampang-penampang tegak. Sebuah pertanyaan kemudian muncul: Apakah metode yang kita gunakan masih tetap berlaku untuk benda-benda yang penampang tegaknya berbentuk bujur sangkar atau segitiga? Jawabannya ya; kita masih dapat menghitung luas penampang-penampang tersebut. Perhatikanlah dua contoh di bawah ini
CONTOH 3:
Andaikan alas sebuah benda adalah suatu daerah rata-rata pada kuadran pertama yang dibatasi oleh \(y=1-x^2/4\), sumbu \(x\) dan sumbu \(y\). Andaikan penampang-penampang yang tegak lurus pada sumbu \(x\) berbentuk bujur sangkar. Tentukan volume benda ini.
Apabila kita potong-potong benda tegak lurus pada sumbu \(x\) kita peroleh lempeng-lempeng tipis yang berbentuk bujursangkar (Gambar 8).

Gambar 8.
Volume benda itu dapat dihitung sebagai berikut.

CONTOH 4:
Dketahui alas sebuah benda merupakan daerah yang dibatasi oleh satu busur kurva \(y=\sin{x}\) dan sumbu \(x\). Tiap penampang yang tegak lurus pada sumbu \(x\) adalah sebuah segitiga sama sisi yang berdiri pada alasnya. Tentukan volume benda itu!

Gambar 9.
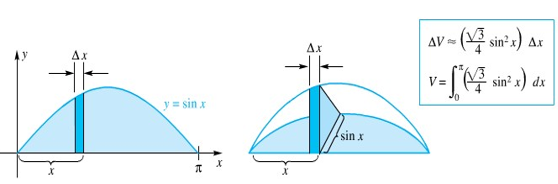
Gambar 10.
Kita ingat bahwa luas segitiga sama sisi dengan panjang sisi \(u\) adalah \( \frac{\sqrt{3}}{4} u^2\) (Gambar 5). Kemudian lihatlah Gambar 10. Untuk melakukan pengintegralan kita menggunakan \(\sin^2{x}= \frac{1-\cos{2x}}{2}\).
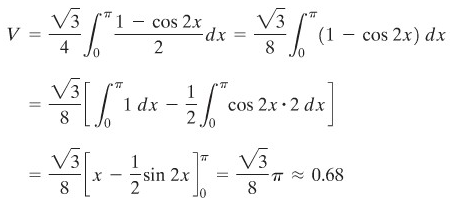
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Beberapa orang memimpikan kesuksesannya, sementara yang lainnya bangun setiap pagi untuk mewujudkan mimpinya.
