Teknik Integral Substitusi Trigonometri

Kalkulus I » Teknik Pengintegralan › Teknik Integral Substitusi Trigonometri

Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Teknik Integral Substitusi Trigonometri

Bentuk akar dalam integran sering kali menimbulkan kesulitan untuk memecahkan integral yang bersangkutan. Dengan substitusi trigonometri yang tepat bentuk akar itu dapat dirasionalkan.

Sering kali kita menjumpai soal integral di mana fungsi yang akan diintegralkan (integran) berupa bentuk akar. Adanya bentuk akar ini acap kali menimbulkan kesulitan untuk memecahkan integral tersebut. Namun, dengan teknik integral yang tepat, kita bisa memecahkan soal integral di mana integrannya berupa bentuk akar ini dengan gampang dan cepat.

Teknik integral yang akan kita bahas yaitu teknik integral substitusi trigonometri. Dengan substitusi trigonometri yang tepat bentuk akar dalam integran dapat dirasionalkan dan karena itu dapat dengan mudah untuk diintegralkan.

Integran yang mengandung \(\sqrt{(a^2-x^2)}, \sqrt{(a^2+x^2)},\) dan \(\sqrt{(x^2-a^2)}\)

Apabila kita menjumpai integran yang fungsinya mengandung ketiga bentuk akar di atas, maka teknik integral substitusi trigonometri dapat diterapkan. Untuk merasionalkan bentuk akar-akar tersebut kita gunakan substitusi berikut:

Dari substitusi tersebut, kita peroleh hasil berikut:

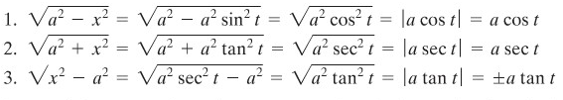
Perhatikan bahwa pembatasan pada \(t\) memungkinkan kita untuk menghilangkan tanda nilai absolut pada dua kasus pertama. Selain itu, pembatasan ini juga membuat fungsi \(\sin, \tan\) dan \(\sec\) menjadi dapat diinverskan.

CONTOH 1:

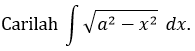
Penyelesaian:

Untuk menyelesaikan soal ini kita gunakan substitusi berikut:

sehingga kita peroleh \(dx = a \cos{⁡t} \ dt\) dan \(\sqrt{a^2-x^2} = a \cos{⁡t}\). Dengan demikian,

Oleh karena \(x = a \sin{t}\) ekivalen dengan \(x/a = \sin⁡{t}\) dan oleh karena selang \(t\) kita batasi sehingga sinus memiliki invers, maka

Dan dengan sebuah kesamaan yang telah kita pelajari mengenai fungsi trigonometri, kita peroleh

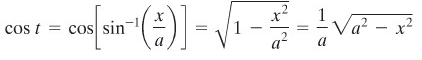
Ini dapat pula dilihat pada Gambar 1 di bawah ini.

Gambar 1.

Dengan demikian,

Dengan hasil yang telah kita peroleh dalam Contoh 1, kita dapat menghitung integral tentu yang menggambarkan luas daerah setengah lingkaran (Gambar 2).

Gambar 2.

CONTOH 2:

Selesaikan \( \displaystyle \int \sqrt{x^2 - a^2} \ dx \).

Pembahasan:

Dengan memisalkan \( x = a \sec t \) kita peroleh hasil berikut:

\begin{aligned} x &= a \sec t \Leftrightarrow \sec t = \frac{x}{a} \\[8pt] \frac{dx}{dt} &= a \sec t \tan t \Leftrightarrow dx = a \sec t \tan t \ dt \\[8pt] \sqrt{x^2 - a^2} &= a \tan t \end{aligned}

Selanjutnya, kita akan gunakan informasi di atas untuk menyelesaikan integral pada soal kita, yakni:

\begin{aligned} \int \sqrt{x^2 - a^2} \ dx &= \int a \tan t \cdot a \sec t \tan t \ dt = a^2 \int \sec t \tan^2 t \ dt \\[8pt] &= a^2 \int \sec t \ (\sec^2 t - 1) \ dt = a^2 \left( \int \sec^3 t \ dt - \int \sec t \ dt \right) \\[8pt] &= a^2 \left( \frac{1}{2} \sec t \tan t + \frac{1}{2} \ln |\sec t + \tan t| - \ln |\sec t + \tan t| \right) \\[8pt] &= a^2 \left( \frac{1}{2} \sec t \tan t - \frac{1}{2} \ln |\sec t + \tan t| \right) \\[8pt] &= \frac{a^2}{2} \sec t \tan t - \frac{a^2}{2} \ln |\sec t + \tan t| \\[8pt] &= \frac{a^2}{2} \cdot \frac{x}{a} \cdot \frac{\sqrt{x^2-a^2}}{a} - \frac{a^2}{2} \ln \left|\frac{x}{a} + \frac{\sqrt{x^2-a^2}}{a} \right| + C \\[8pt] &= \frac{x}{2} \sqrt{x^2-a^2} - \frac{a^2}{2} \ln \left|\frac{x + \sqrt{x^2-a^2}}{a} \right| + C \\[8pt] &= \frac{x}{2} \sqrt{x^2-a^2} - \frac{a^2}{2} \left( \ln \left|x + \sqrt{x^2-a^2} \right| - \ln|a| \right) + C \\[8pt] &= \frac{x}{2} \sqrt{x^2-a^2} - \frac{a^2}{2} \ln \left|x + \sqrt{x^2-a^2} \right| + \frac{a^2}{2} \ln|a| + C \\[8pt] &= \frac{x}{2} \sqrt{x^2-a^2} - \frac{a^2}{2} \ln \left|x + \sqrt{x^2-a^2} \right| + K \\[8pt] &= \frac{1}{2} \left( \sqrt{x^2-a^2} - a^2 \ln \left|x + \sqrt{x^2-a^2} \right| \right) + K \end{aligned}

Jadi, hasil dari \(\int \sqrt{x^2-a^2} \ dx \), yaitu:

\begin{aligned} \int \sqrt{x^2 - a^2} \ dx &= \frac{1}{2} \left( \sqrt{x^2-a^2} - a^2 \ln \left|x + \sqrt{x^2-a^2} \right| \right) + K \end{aligned}

Keterangan:

Untuk mencari nilai \( \tan t\), kita bisa gambarkan segitiga siku-siku berdasarkan pemisalan yang kita buat di awal tadi. Selanjutnya kita cari sisi lain dari segitiga siku-siku yang lain menggunakan Rumus Phytagoras. Berikut hasil yang kita peroleh:

CONTOH 3:

Selesaikan \( \displaystyle \int \sqrt{a^2 + x^2} \ dx \).

Pembahasan:

Dengan memisalkan \( x = a \tan t \) kita peroleh hasil berikut:

\begin{aligned} x &= a \tan t \Leftrightarrow \tan t = \frac{x}{a} \\[8pt] \frac{dx}{dt} &= a \sec^2 t \Leftrightarrow dx = a \sec^2 t \ dt \\[8pt] \sqrt{a^2 + x^2} &= a \sec t \end{aligned}

Selanjutnya, kita akan gunakan informasi di atas untuk menyelesaikan integral pada soal kita, yakni:

\begin{aligned} \int \sqrt{a^2 + x^2} \ dx &= \int a \sec t \cdot a \sec^2 t \ dt = a^2 \int \sec^3 t \ dt \\[8pt] &= a^2 \left( \frac{1}{2} \sec t \tan t + \frac{1}{2} \ln|\sec t + \tan t| \right) \\[8pt] &= \frac{a^2}{2} \sec t \tan t + \frac{a^2}{2} \ln|\sec t + \tan t| \\[8pt] &= \frac{a^2}{2} \cdot \frac{\sqrt{a^2 + x^2}}{a} \cdot \frac{x}{a} + \frac{a^2}{2} \ln \left|\frac{\sqrt{a^2 + x^2}}{a} + \frac{x}{a} \right| + C \\[8pt] &= \frac{x}{2} \sqrt{a^2 + x^2} + \frac{a^2}{2} \ln \left|\frac{x + \sqrt{a^2 + x^2}}{a} \right| + C \\[8pt] &= \frac{x}{2} \sqrt{a^2 + x^2} + \frac{a^2}{2} \ln \left|x + \sqrt{a^2 + x^2} \right| - \frac{a^2}{2} \ln |a| + C \\[8pt] &= \frac{x}{2} \sqrt{a^2 + x^2} + \frac{a^2}{2} \ln \left|x + \sqrt{a^2 + x^2} \right| + K \\[8pt] &= \frac{1}{2} \left( \sqrt{a^2 + x^2} + a^2 \ln \left|x + \sqrt{a^2 + x^2} \right| \right) + K \end{aligned}

Jadi, hasil dari \(\int \sqrt{a^2+x^2} \ dx \), yaitu:

\begin{aligned} \int \sqrt{a^2 + x^2} \ dx &= \frac{1}{2} \left( \sqrt{a^2 + x^2} + a^2 \ln \left|x + \sqrt{a^2 + x^2} \right| \right) + K \end{aligned}

Keterangan:

Untuk mencari nilai \( \sec t\), kita bisa gambarkan segitiga siku-siku berdasarkan pemisalan yang kita buat di awal tadi. Selanjutnya kita cari sisi lain dari segitiga siku-siku yang lain menggunakan Rumus Phytagoras. Berikut hasil yang kita peroleh:

CONTOH 4:

Penyelesaian:

Misalkan \(x =3 \tan{⁡t}, -π/2 < t < π/2\), maka \(dx = 3 \sec^2⁡{t} \ dt\) dan \(\sqrt{(9+x^2)}=3 \sec⁡{t}\).

Langkah terakhir adalah menyelesaikan integral \(\sec{t}\). Karena kita memisalkan \(x = 3 \tan{t}\), maka sekarang \(\tan{t} = x/3\), yang memberikan sebuah segitiga seperti terlihat pada Gambar 3. Dari Gambar 3, kita menyimpulkan bahwa \(\sec{⁡t}=\sqrt{(9+x^2)}/3\). Dengan demikian,

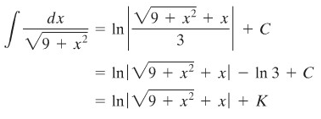
Gambar 3

CONTOH 5:

Penyelesaian:

Andaikan \(x = 2 \sec{⁡t}\), dengan \(0 ≤ t ≤ π/2\). Selang \(t\) ini kita peroleh berhubung selang \(x\) adalah \(2 ≤ x ≤ 4\). (Gambar 4). Hal ini penting sebab kita dapat menghilangkan tanda nilai mutlak yang muncul apabila kita menyederhanakan \(\sqrt{x^2-a^2}\). Dalam kasus kita, didapatkan

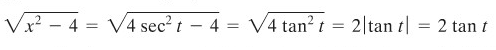
Sekarang kita gunakan teorema mengenai substitusi dalam integral tentu yang mengharuskan perubahan batas-batas integral. Jadi kita peroleh

Gambar 4

Melengkapkan Menjadi kuadrat

Apabila sebuah bentuk kuadrat \(x^2+Bx+C\) muncul di bawah akar dalam integran, kita dapat melengkapkannya menjadi kuadrat sebelum kita menggunakan substitusi trigonometri. Simak contoh berikut ini.

CONTOH 6:

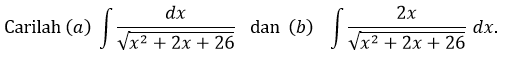
Penyelesaian:

\( x^2+2x+26=x^2+2x+1+25=(x+1)^2+25. \)

Misalkan \(u=x+1\) dan \(du=dx\), maka

Selanjutnya misalkan \(u = 5 \tan{t}, -π/2 < t < π/2\), maka \(du= 5 \sec^2⁡t \ dt\) dan \(\sqrt{μ^2+25}=\sqrt{25(\tan^2⁡t+1)} = 5 \sec{⁡t}\), sehingga

Untuk mengatasi integral kedua, kita tuliskan

Integral yang pertama pada ruas kanan diselesaikan dengan substitusi \(u=x^2+2x+26\); sedangkan integral yang kedua barus saja kita selesaikan. Kita peroleh,

Integran yang Memuat \(\sqrt[n]{ax+b}\).

Selain ketiga bentuk akar yang telah kita bahas di atas, bentuk akar di dalam integran yang sering kita jumpai yaitu \(\sqrt[n]{ax+b}\). Untuk merasionalkan bentuk akar ini kita tidak perlu menggunakan substitusi trigonometri. Cukup dengan substitusi \(u = \sqrt[n]{ax+b}\) maka bentuk akar dalam integran dapat dirasionalkan.

Perhatikan contoh di bawah ini.

CONTOH 7:

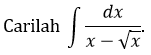
Penyelesaian:

Misalkan \(u=\sqrt{x}\), maka \(u^2=x\) dan \(2u \ du=dx\). Dengan demikian, kita peroleh

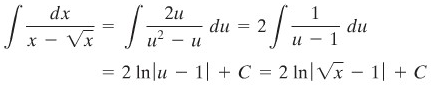
CONTOH 8:

Penyelesaian:

Misalkan \(u = \sqrt[3]{x-4}\), maka \(u^3=x-4\) dan \(3u^2 \ du=dx\). Dengan demikian, kita peroleh

CONTOH 9:

Penyelesaian:

Misalkan \(u=(x+1)^{1/5}\), maka \(u^5=x+1\) dan \(5u^4 \ du=dx\). Dengan demikian, kita peroleh

Sumber:

Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.

Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.

www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

Kalkulus I » Teknik Pengintegralan › Teknik Integral Substitusi Trigonometri