www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Fungsi Gamma dan Fungsi Beta › Fungsi Gamma dan Fungsi Beta
Fungsi Gamma dan Fungsi Beta
Fungsi gamma merupakan perluasan dari fungsi faktorial. Sementara itu, fungsi beta dikenal juga sebagai integral Euler jenis pertama dan terkait erat dengan fungsi gamma.
Fungsi gamma merupakan perluasan dari fungsi faktorial. Fungsi ini sering kita jumpai dalam persamaan-persamaan peluang dan statistika. Sementara itu, fungsi beta dikenal juga sebagai integral Euler jenis pertama dan terkait erat dengan fungsi gamma.
Pada artikel ini, kita akan mempelajari fungsi gamma dan fungsi beta serta kaitan di antara keduanya.
Fungsi Gamma
Seperti disebutkan di atas, fungsi gamma merupakan perluasan dari fungsi faktorial, yang mana kita definisikan sebagai berikut.
Fungsi Gamma
Fungsi Gamma didefinisikan sebagai
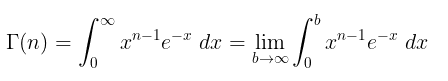
yang mana konvergen untuk \(n > 0\).
Rumus berulang untuk fungsi Gamma diberikan oleh

di mana \(Γ(1)=1\) dan rumus untuk \(n\) faktorial (\(n!\)) yaitu

Di bawah ini kita akan membuktikan rumus berulang untuk fungsi gamma.
#1. Bukti bahwa \(Γ(n+1)=n \ Γ(n), n>0\):

#2. Bukti bahwa \(Γ(n+1)=n!\), \(n=1,2,3,…\)
Pertama kita mulai dengan membuktikan bahwa \(Γ(1)=1\) yang diberikan berikut ini.

Selanjutnya, untuk \(n=2,3,4,… \), kita gunakan hubungan \(Γ(n+1)=n \ Γ(n)\)

Sehingga, secara umum \(Γ(n+1)=n Γ(n)=n!\) untuk n bilangan bulat positif.
Sebagai contoh, perhatikan hasil perhitungan berikut ini.

Perhatikan kembali hasil di atas. Dalam beberapa kasus kita akan sering menjumpai \(Γ(1/2)=\sqrt{\pi}\). Karena pembuktiannya melibatkan prosedur integral lipat dua yang mana belum kita pelajari, maka untuk sementara hafalkan saja hasil tersebut.
Fungsi Gamma untuk \( n < 0 \)
Untuk mencari nilai fungsi Gamma di mana \(n < 0\), kita dapat gunakan hubungan berikut.

Sebagai contoh, kita akan mencari nilai \( Γ(-1/2) \). Kita peroleh sebagai berikut:
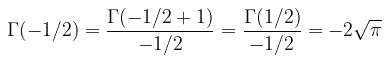
Fungsi Beta
Fungsi beta disebut juga integral Euler jenis pertama, dan terkait erat dengan fungsi gamma. Adapun fungsi beta didefinisikan sebagai berikut.
Fungsi Beta
Fungsi beta didefinisikan sebagai

yang mana konvergen untuk \(m > 0\) dan \(n > 0\).
Dalam fungsi Beta, nilai \(B(m,n)\) akan sama dengan \(B(n,m)\).
Hubungan antara Fungsi Gamma dan Fungsi Beta
Terdapat hubungan antara fungsi Gamma dan fungsi Beta yakni

Pembuktian untuk hubungan antara fungsi gamma dan beta ini mengharuskan kita memahami integral lipat dua yang belum kita pelajari. Oleh karena itu, untuk sementara kita abaikan dulu pembuktian ini dan cukup hafalkan saja hubungan tersebut.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Janganlah engkau mengucapkan perkataan yang engkau sendiri tak suka mendengarnya jika orang lain mengucapkannya kepadamu.
