Kalkulus I   »   Fungsi   ›  Fungsi Logaritma dan Logaritma Natural

Fungsi Logaritma dan Logaritma Natural

Fungsi logaritma natural adalah fungsi logaritma dengan basis nya adalah bilangan e yang merupakan bilangan irrasional atau tak rasional.

Dari pelajaran aljabar kita tahu bahwa sebuah logaritma adalah sebuah eksponen. Lebih tepatnya, jika \(b > 0\) dan \(b≠1\), maka untuk nilai positif \(x\), ekspresi

(dibaca “logaritma dengan basis \(b\) dari \(x\)”) menunjukkan bahwa eksponen di mana \(b\) harus ditingkatkan untuk menghasilkan \(x\). Dengan demikian, misalnya,

Kita sebut fungsi \(f(x)=\log_b⁡ x \) sebagai fungsi logaritma dengan basis \(b\).

Fungsi logaritma juga bisa dipandang sebagai invers fungsi eksponensial. Untuk melihat kenapa bisa demikian, amatilah Gambar 1 bahwa jika \(b > 0\) dan \(b≠1\), maka grafik \(f(x)=b^x\) melewati uji garis horisontal, sehingga \(b^x\) mempunyai sebuah invers. Kita bisa mencari sebuah formula untuk invers ini dengan \(x\) sebagai independent variabel dengan menyelesaikan persamaan

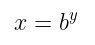
untuk \(y\) sebagai fungsi dari \(x\). Tetapi persamaan ini menyatakan bahwa \(y\) merupakan logaritma dengan basis \(b\) dari \(x\), sehingga bisa dituliskan sebagai

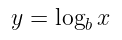
Gambar 1

Dengan demikian, kita telah membangun hasil berikut

Dari teorema ini maka grafik \(y=b^x\) dan \(y=\log_b⁡x\) merupakan cerminan dari satu sama lain terhadap garis \(y = x\) (lihat Gambar 1 untuk kasus di mana \(b > 1\)).

Gambar 2 menunjukkan grafik \(y=\log_b⁡x\) untuk berbagai nilai \(b\). Amatilah bahwa mereka semua melewati titik (1,0).

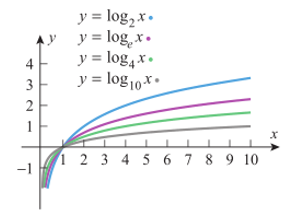
Gambar 2

Sifat-sifat Aljabar Logaritma

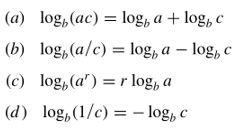
Logaritma Natural

Untuk bilangan positif \(a\), nilai fungsi \(f(x)=a^x\) mudah ditentukan ketika \(x\) adalah bilangan bulat atau bilangan rasional. Ketika \(x\) tidak rasional, makna \(a^x\) tidak begitu jelas. Demikian pula, definisi logaritma \(\log_a⁡x\), fungsi invers dari \(f(x)=a^x\), tidak sepenuhnya jelas.

Sekarang kita akan berkenalan dengan logaritma dengan basis nya adalah bilangan \(e\) yang merupakan bilangan irrasional atau tak rasional. Ini disebut logaritma natural karena fungsi \(\log_e⁡x\) merupakan invers dari fungsi eksponensial natural \(e^x\). Penulisan standar untuk logaritma natural adalah dengan \(\ln x\). Misalnya,

Secara umum,

Grafik Fungsi Logaritma Natural

Fungsi logaritma natural \(f(x)=\ln ⁡x\) adalah fungsi yang menaik (increasing function) dan grafiknya cekung ke bawah (concave down). Selain itu, fungsi logaritma natural adalah fungsi yang kontinu. Perhatikan Gambar 3 di bawah ini.

Gambar 3. Grafik fungsi logaritma

Daerah asal (domain) \(\ln x\) terdiri dari himpunan semua bilangan riil positif, sehingga grafik \(y = \ln x\) terletak di sebelah kanan setengah bidang.

Sifat-Sifat Fungsi Logaritma Natural

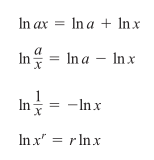
Sumber:

Anton, Howard., et al. (2012). Calculus, 10th ed. Hoboken: John Wiley & Sons, Inc.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.