CONTOH 1:

Carilah \( \displaystyle{\lim_{x \to 3}\, 2x^4 } \).

Penyelesaian:

CONTOH 2:

Carilah \( \displaystyle{\lim_{x \to 4}\, (3x^2-2x) } \).

Penyelesaian:

CONTOH 3:

Carilah \( \displaystyle{\lim_{x \to 4}\, \frac{\sqrt{x^2+9}}{x} } \).

Penyelesaian:

CONTOH 4:

Jika \( \displaystyle{\lim_{x \to 3}\, f(x) = 4 } \) dan \( \displaystyle{\lim_{x \to 3}\, g(x) = 8 } \), carilah \( \displaystyle{\lim_{x \to 3}\, \left[ f^2(x) \cdot \sqrt[3]{g(x)} \right] } \)

Penyelesaian:

CONTOH 5:

Carilah \( \displaystyle{\lim_{x \to 2}\, \frac{7x^5-10x^4-13x+6}{3x^2-6x-8} } \).

Penyelesaian:

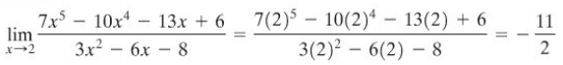
CONTOH 6:

Carilah \( \displaystyle \lim_{x \to 1} \, \frac{x^3+3x+7}{x^2-2x+1} \).

Penyelesaian:

Perhatikan bahwa

Baik Teorema B maupun Pernyataan 7 dalam Teorema A tidak berlaku, karena limit dari penyebut bernilai 0. Tetapi, karena limit pembilang adalah 11, kita lihat bahwa selama \(x\) dekat 1, kita membagi sebuah bilangan dekat 11 dengan sebuah bilangan positif dekat 0.

Hasilnya adalah sebuah bilangan positif yang besar. Kenyataannya, bilangan yang dihasilkan dapat dibuat besar sekehendak kita dengan membiarkan \(x\) cukup dekat ke 1. Kita katakan bahwa limit tersebut adalah \(+∞\).

CONTOH 7:

Carilah \( \displaystyle{\lim_{x \to 1}\, \frac{x-1}{\sqrt{x}-1} } \).

Penyelesaian:

CONTOH 8:

Carilah \( \displaystyle{\lim_{x \to 2}\, \frac{x^2+3x-10}{x^2+x-6} } \).

Penyelesaian:

Teorema B tidak berlaku karena penyebutnya adalah 0 saat \(x = 2\). Saat kita mensubstitusikan \(x = 2\) pada pembilang kita juga mendapatkan 0, sehingga hasil bagi mengambil bentuk tanpa arti 0/0 di \(x = 2\). Ketika ini terjadi kita seharusnya mencari bentuk penyederhanaan dengan cara faktorisasi.

Bagian kedua dari persaman sesuai dengan Teorema C karena

untuk semua \(x\) kecuali \(x = 2\). Saat kita menerapkan Teorema C, kita bisa mengevaluasi limitnya dengan substitusi (misalnya, dengan menerapkan Teorema B).